笛卡尔树

news/2025/1/13 17:49:54/文章来源:https://www.cnblogs.com/Baiyj/p/18242908

笛卡尔树

引入

笛卡尔树是一种二叉树，每一个节点由一个键值二元组\((k,w)\)构成。要求k满足二叉搜索树的性质，而w满足堆的性质。 一个有趣的事实是，如果笛卡尔树的\(k,w\)键值确定，且k互不相同，w互不相同，那么这个笛卡尔树的结构是唯一的。

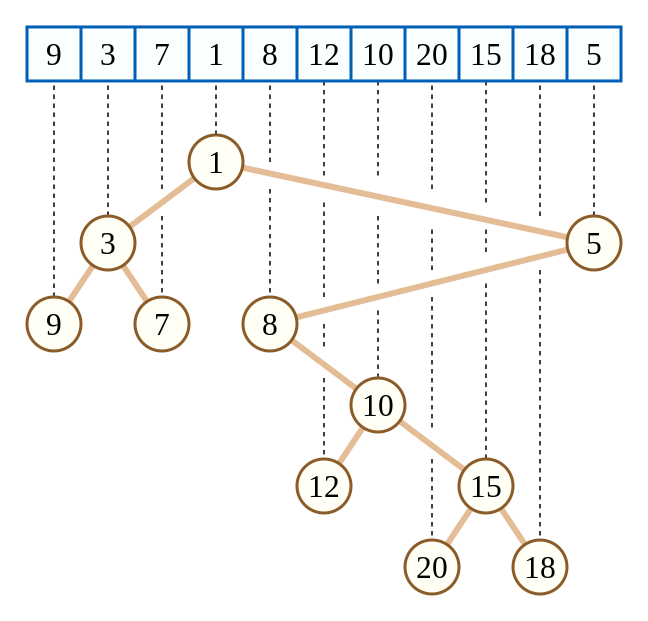
上面这棵笛卡尔树相当于把数组元素当作键值w，而把数组下标当作键值k。显然可以发现，这棵树的键值k满足二叉搜索树的性质，而键值w满足小根堆的性质。
其实图中的笛卡尔树是一种特殊的情况，因为二元组的键值k恰好对应数组下标，这种特殊的笛卡尔树有一个性质，就是一棵子树内的下标是一个连续的区间（这样才能满足二叉搜索树的性质）。更一般的情况则是任意二元组构建的笛卡尔树。

构建

栈构建

过程

我们考虑将元素按照键值k排序。然后一个一个插入到当前的笛卡尔树中。那么每次我们插入的元素必然在这个树的右链（从根节点一直往右子树走形成的链）的末端。于是我们执行这样一个过程，从下往上比较右链节点与当前节点u的w，如果找到了一个右链上的节点x满足\(x_w<u_w\)，就把u接到x的右儿子上，而x原本的右子树就变成u的左子树。

显然每个数最多进出右链一次（或者说每个点在右链中存在的是一段连续的时间）。这个过程我们可以用栈维护，栈中维护当前笛卡尔树的右链上的节点。一个点不在右链上了就把它弹掉。这样每个点最多进出一次，复杂度\(O(n)\)。

笛卡尔树与treap

treap其实是笛卡尔树的一种，只不过w的值完全随机。treap也有线性的构建算法，如果提前将元素排好序，显然可以使用上述单调栈算法完成构建过程，只不过很少会这么用。

例题1：【模板】笛卡尔树

板子。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const int N = 1e7 + 3;
int n, a[N], d[N];
int stk[N], top;
int ls[N], rs[N];
ll lans, rans;
inline void build() {for (rg int i = 1; i <= n; i++) {while (top && a[stk[top]] > a[i]) ls[i] = stk[top--];if (top) rs[stk[top]] = i;stk[++top] = i;}
}
int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> n;for (rg int i = 1; i <= n; i++) {cin >> a[i];}build();for (rg int i = 1; i <= n; i++) {lans ^= 1ll * i * (ls[i] + 1);rans ^= 1ll * i * (rs[i] + 1);}cout << lans << " " << rans << "\n";return qwq;
}

例题2：HDU1506 最大子矩形

我们把下标作为键值k，\(h_i\)作为键值w满足小根堆性质，构建一颗\((i,h_i)\)的笛卡尔树。
这样我们枚举每个节点u，把\(u_w\)（即高度值h）作为最大子矩阵的高度。由于我们建立的笛卡尔树满足小根堆性质，因此u的子树内的节点的高度都大于等于u。而我们又知道u子树内的下标是一段连续区间。于是我们只需要知道子树的大小，然后就可以算这个区间的最大子矩阵的面积了。用每一个点计算出来的值更新答案即可。显然这个可以一次dfs完成，因此复杂度是\(O(n)\)的。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long 
using namespace std;
const int N = 1e5 + 3;
int n;
int top, stk[N];
int v[N], ls[N], rs[N];
ll ans;
inline void build() {stk[++top] = 0;  //为了保证笛卡尔树的根节点是0的右儿子，便于dfs for (rg int i = 1; i <= n; i++) {while (top && v[stk[top]] > v[i]) ls[i] = stk[top--];if (top) rs[stk[top]] = i;stk[++top] = i;}
}
inline int dfs(int x) {  //一次dfs更新答案就可以了if (!x) return qwq;rg int siz = dfs(ls[x]);siz += dfs(rs[x]);ans = max(ans, (ll)(siz + 1) * v[x]);return siz + 1;
}
int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);while (cin >> n && n) {memset(ls, 0, sizeof(ls));memset(rs, 0, sizeof(rs));memset(stk, 0, sizeof(stk));top = 0;for (rg int i = 1; i <= n; i++) {cin >> v[i];}build();ans = 0;dfs(rs[0]);cout << ans << "\n";}return qwq;
}

例题3：[TJOI2011] 树的序

题目中的输入要满足二叉搜索树的性质，所以对应键值k。于是令i值为键值w，建立笛卡尔树。
因为要求字典序最小，而二叉搜索树又满足左儿子<父节点<右儿子，所以先序遍历输出即可。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 1e5 + 3;
int n;
int a[N], stk[N], top;
int ls[N], rs[N];
inline void build() {stk[++top] = 0;for (rg int i = 1; i <= n; i++) {while (top && a[stk[top]] > a[i]) ls[i] = stk[top--];if (top) rs[stk[top]] = i;stk[++top] = i;}
}
inline void dfs(int rt) {if(!rt) return ;cout << rt << " ";dfs(ls[rt]);dfs(rs[rt]);
}
int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> n;for (rg int i = 1; i <= n; i++) {rg int v;cin >> v;a[v] = i;}build();dfs(rs[0]);return qwq;
}

例题4：[hdu6305]RMQ Similar Sequence

如果A和B是RMQ Similar，则A和B的笛卡尔树同构。因为B中的每个数是\(0\sim1\)之间的实数，因此出现相同数字的概率近似为0，可以假设B中每个数都不同。设A的笛卡尔树每个子树的大小为\(siz[i]\)，则任一B排列与A同构的概率是\(\displaystyle\prod_1^n\frac{1}{siz[i]}\)。因为B中每个数满足均匀分布，因此期望值为\(\frac1 2\)，和的期望值为\(\frac n 2\)，因此满足于A同构的B中所有数之和的期望为\(\displaystyle\frac{n}{2\prod_1^n siz[i]}\)。
注意：
1.最后答案为分数形式，又要取模，因此要求逆元。
2.因为要求的是区间的最大值，因此要满足大根堆性质，即要求a[stk[top]] < a[i]。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 1e6 + 3, mod = 1e9 + 7;
int T, n;
int a[N], stk[N], top;
int ls[N], rs[N];
inline void init() {top = 0;for (rg int i = 1; i <= n; i++) ls[i] = rs[i] = 0;
}
inline void build() {for (rg int i = 1; i <= n; i++) {while (top && a[stk[top]] < a[i]) ls[i] = stk[top--];if (top) rs[stk[top]] = i;stk[++top] = i;}
}
int siz[N];
inline int dfs(int rt) {  //求子树大小 if (!rt) return qwq;rg int res = dfs(ls[rt]);res += dfs(rs[rt]);res++;siz[rt] = res;return res;
}
inline int qpow(int a, int b) {rg int res = 1;while (b) {if (b & 1) res = res * a % mod;a = a * a % mod;b >>= 1;}return res;
}
inline int inv(int a) {return qpow(a, mod - 2);
}
signed main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> T;while (T--) {init();cin >> n;for (rg int i = 1; i <= n; i++) {cin >> a[i];}build();dfs(stk[1]);rg int ans = 2;for (rg int i = 1; i <= n; i++) {ans = ans * siz[i] % mod;}cout << n * inv(ans) % mod << "\n";}return qwq;
}

例题5：[COCI2008-2009#4] PERIODNI

我们每次尽可能地删去整张表格的最低行，直到当前最低行已经不连通。将删去的行组成一个矩形，再将分开的至多两个连通块递归处理，就可以将原图分成若干个矩形。
样例3分成矩形后的图如下：

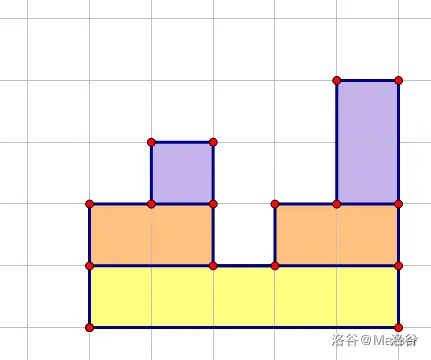
我们发现，这样构成的若干个矩形正好对应笛卡尔树上的所有节点，每次递归处理的两个小联通块正好是当前节点的两个儿子。根据定义，我们可以知道，对于节点x代表的矩形，它的长度为\(siz_x\)，高度为\(h_x-h_{son_x}\)。
这样，我们建出笛卡尔树，就可以把这一问题转化成书上背包问题。
定义\(f_{i,j}\)表示在子节点i子树所代表的区域内选择了j个格子的方案数，两个儿子的答案显然可以用树形背包合并，难点就只剩下如何计算与合并当前节点的方案了。
枚举当前节点所代表的矩形选了j个格子，子树内其余部分选了k个格子，我们可以将当前矩形的方案数表示成\(C_{siz_x-k}^{j}\times C_{h_x-h_{son_x}}^{j} \times j!\)，也就是选择行、列的方案数乘上j的全排列。
通过树上背包的siz优化，我们保证两个节点总是在它的LCA处合并。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 503, M = 1e6 + 3, mod = 1e9 + 7;
int n, m;
int h[N], stk[N], top;
int ls[N], rs[N];
int f[N][N], siz[N];
int jie[M];
inline int qpow(int a, int b) {rg int res = 1;while (b) {if (b & 1) res = res * a % mod;a = a * a % mod;b >>= 1;}return res;
}
inline void init() {jie[0] = 1;for (rg int i = 1; i < M; i++) {jie[i] = jie[i - 1] * i % mod;}
}
inline int inv(int a) {return qpow(a, mod - 2);
}
inline int C(int a, int b) {return jie[a] * inv(jie[b]) % mod * inv(jie[a - b]) % mod;
}
inline void build() {for (rg int i = 1; i <= n; i++) {while (top && h[stk[top]] > h[i]) ls[i] = stk[top--];if (top) rs[stk[top]] = i;stk[++top] = i;}
}
inline void dfs(int u, int fath) {if (!u) return ;f[u][0] = 1;siz[u] = 1;rg int k = h[u] - h[fath];  //矩形的宽dfs(ls[u], u);siz[u] += siz[ls[u]];for (rg int i = min(siz[u], m); i; i--) {  //当前子树选的格子数 for (rg int j = 1; j <= min(siz[ls[u]], i); j++) {  //儿子的子树选的格子数 f[u][i] = (f[u][i] + f[ls[u]][j] * f[u][i - j]) % mod;}}dfs(rs[u], u);siz[u] += siz[rs[u]];for (rg int i = min(siz[u], m); i; i--) {for (rg int j = 1; j <= min(siz[rs[u]], i); j++) {f[u][i] = (f[u][i] + f[rs[u]][j] * f[u][i - j]) % mod;}}for (rg int i = min(siz[u], m); i; i--) {  //当前子树选的格子数 for (rg int j = 1; j <= min(k, i); j++) {  //当前节点所代表的矩形选了j个格子，即j行f[u][i] = (f[u][i] + f[u][i - j] * C(siz[u] - (i - j), j) % mod * C(k, j) % mod * jie[j] % mod) % mod;}}
}
signed main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> n >> m;init();for (rg int i = 1; i <= n; i++) {cin >> h[i];}build();dfs(stk[1], 0);cout << f[stk[1]][m] << "\n";return qwq;
}

例题6：[hdu4125]Moles

建笛卡尔树，dfs找出遍历顺序（即欧拉序），然后kmp匹配即可。
编号符合二叉搜索树性质。
根据题意，鼹鼠的编号满足二叉搜索树性质，于是编号为数组下标。又要求先经过编号小的节点，可知要统计欧拉序（因为满足二叉搜索树的性质，所以能保证编号小的节点在左子树上）。
统计出欧拉序后，将其作为文本串，与模式串进行匹配，使用KMP即可。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 6e5 + 3;
int T, n;
int a[N], ls[N], rs[N];
int top, stk[N];
string s, t;
inline void init() {top = 0;for (rg int i = 1; i <= n; i++) {ls[i] = rs[i] = 0;}s = "";
}
inline void build() {for (rg int i = 1; i <= n; i++) {while (top && a[stk[top]] > a[i]) ls[i] = stk[top--];if (top) rs[stk[top]] = i;stk[++top] = i;}
}
inline void add(int u) {if (u & 1) s += '1';else s += '0';
}
inline void dfs(int u) {add(u);if (ls[u]) {dfs(ls[u]);add(u);}if (rs[u]) {dfs(rs[u]);add(u);}
}
int nxt[N];
inline void get_next() {  //在模式串上找失配指针rg int j = 0, k = -1;nxt[0] = -1;rg int lent = t.length();while (j < lent) {if (k == -1 || t[j] == t[k]) {  //如果当前位匹配，j、k都向右移继续匹配 j++;k++;if (t[j] == t[k]) nxt[j] = nxt[k];  //因为如果这一位匹配不上，那么这一位的失配指针也匹配不上，直接跳到最早出现的位置 else nxt[j] = k;} else k = nxt[k];}
}
inline int KMP() {rg int i = 0, j = 0, cnt = 0;rg int lens = s.length(), lent = t.length();get_next();while (i < lens) {if (j == -1 || s[i] == t[j]) {  //这一位匹配成功，向右移继续匹配 i++;j++;} else j = nxt[j];if (j == lent) {  //如果当前匹配成功的长度与模式串长度相等，cnt++，跳指针匹配下一次 cnt++;j = nxt[j];}}return cnt;
}
int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> T;for (rg int tt = 1; tt <= T; tt++) {init();cin >> n;for (rg int i = 1; i <= n; i++) {rg int d;cin >> d;a[d] = i;}cin >> t;build();dfs(stk[1]);cout << "Case #" << tt << ": " << KMP() << "\n";}return qwq;
}

例题7：[hdu6854]Kcats

a[]就是右链的长度。
区间dp。

【颓题解】
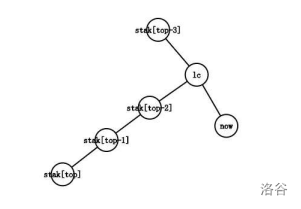
\(a_i\)为最后的笛卡尔树上，第i个节点的所有祖先中k值比自己小的节点的数量。接着考虑区间dp，令\(f_{l,r,d}\)表示区间\([l,r]\)所对应的笛卡尔树的根节点的祖先中有d个k值比自己小。那么它的左儿子节点，即区间\([l,rt)\)的根节点的有贡献的祖先节点一定和它的祖先节点是一样的。但是它的右儿子节点，即区间\((rt,r]\)的根节点不仅有它有的祖先节点，还包含它本身。因为笛卡尔树满足小根堆，所以它的左子树一定比它大且按顺序排列，因此数字的组合可能为\(C_{r-l}^{k-l}\)。转移方程为：

\[f_{l,r,d}=\displaystyle\sum_{k-i}^{j} \begin{cases} \sum_{d=a_k}f_{l,k-1,d}\times f_{k+1,r,d+1}\times C_{r-l}^{k-l}(a_k\ne -1) \\ \sum_{d=1}^{n}f_{l,k-1,d}\times f_{k+1,r,d+1}\times C_{r-1}^{k-l}(a_k=-1) \end{cases} \]

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 103, mod = 1e9 + 7;
int T, n, ll, rr;
int a[N];
int f[N], g[N], dp[N][N][N];
inline int qpow(int a, int b) {rg int res = 1;while (b) {if (b & 1) res = res * a % mod;a = a * a % mod;b >>= 1;}return res;
}
inline void get() {f[0] = 1;for (rg int i = 1; i < N; i++) {f[i] = f[i - 1] * i % mod;}g[N - 1] = qpow(f[N - 1], mod - 2);for (rg int i = N - 2; i >= 0; i--) {g[i] = g[i + 1] * (i + 1) % mod;}
}
inline int C(int a, int b) {return f[a] * g[b] % mod * g[a - b] % mod;
}
inline void init() {for (rg int i = 1; i <= n; i++) {for (rg int j = 1; j <= n; j++) {for (rg  int k = 1; k <= n; k++) dp[i][j][k] = 0;}}
}
signed main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);get();cin >> T;while (T--) {cin >> n;init();for (rg int i = 1; i <= n; i++) cin >> a[i];for (rg int len = 1; len <= n; len++) {for (rg int l = n - len + 1; l >= 1; l--) {rg int r = l + len - 1;for (rg int k = l; k <= r; k++) {if (a[k] == -1) {ll = 1;rr = n;} else {ll = rr = a[k];}for (rg int d = ll; d <= rr; d++) {dp[l][r][d] = (dp[l][r][d] + (l < k ? dp[l][k - 1][d] : 1) * (k < r ? dp[k + 1][r][d + 1] : 1) % mod * C(r - l, k - l) % mod) % mod;}}}}cout << dp[1][n][1] << "\n";}return qwq;
}

完结撒花~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/723301.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

虚树

虚树

虚树 什么是虚树 虚树常常被用在树形\(dp\)中。当一次询问仅仅涉及到整棵树中少量节点时为每次询问都对整棵树进行\(dp\)在时间上是不可接受的。此时，我们建立一棵仅仅包含部分关键节点的虚树，将非关键节点构成的链简化成边或是剪去，在虚树上进行\(dp\)。 虚树包含所有的询问…
阅读更多...
矩阵乘法与矩阵快速幂

矩阵乘法与矩阵快速幂

1 矩阵乘法 1.定义 若矩阵A的大小为\(n \times m\)，矩阵B的大小为\(m \times p\)，则两个矩阵可以做乘法，得到的矩阵C的大小为\(n \times p\)。 \[A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{bmatrix} \]\[B = \begin{…
阅读更多...
状压dp

状压dp

状压dp 1.状态压缩 状态压缩就是使用某种方法，以最小的代价来表示某种状态，通常是用一串01数字（二进制数）来表示各个点的状态。这就要使用状态压缩的对象的点的状态只有两种：0和1。 2.使用条件 1.解法需要保存一定的状态数据（表示一种状态的一个数据值），每个状态通常情…
阅读更多...
Redis之哨兵模式

Redis之哨兵模式

概述无哨兵模式的主从切换的方法是当主服务器宕机后，需要手动把一台从服务器切换为主服务器，这就需要人工干预，费时费力，还会造成一段时间内服务不可用。这不是一种推荐的方式，更多时候，我们优先考虑哨兵模式。 Redis从2.8开始正式提供了Sentinel(哨兵)架构来解决这个问题…
阅读更多...
ibus-libpinyin无法使用中括号下一页（未解决）

ibus-libpinyin无法使用中括号下一页（未解决）

问题 中括号切换上下页用惯了，使用这个不能【】真不习惯。 SunPinyin sunpinyin可以[]切换，但是【】本身变成其他字符了。 不能使用shift将半路的中文换为英文。比如我打拼音，输入完后按shift，我希望他变成英文，并且切换到英文。 搜狗输入法 系统是Ubuntu 22.04 搞了半天用…
阅读更多...
m基于FPGA的FIR低通滤波器实现和FPGA频谱分析,包含testbench和滤波器系数MATLAB计算程序

m基于FPGA的FIR低通滤波器实现和FPGA频谱分析,包含testbench和滤波器系数MATLAB计算程序

1.算法仿真效果 本系统进行了Vivado2019.2平台的开发，Vivado2019.2仿真结果如下：整体仿真结果如下：放大看，滤波效果如下：对应的频谱如下：FPGA的RTL结构如下：最后用matlab对比仿真，结果如下：可以看到，FPGA的滤波效果和频谱分析与matlab的结果一致。2.算法涉及理论知识…
阅读更多...
ch6 信息商品

ch6 信息商品

ch6 信息商品课程目标熟悉信息商品的形成和信息劳动价值理论 掌握信息商品的特征分析及信息商品的价格理论 运用信息商品价格理论分析和理解相关案例多看两眼 ppt 吧，这一部分考的很多 知识回顾 信息商品的概念信息成为商品的基本条件 不宜成为信息商品的信息产品类型 信息商品…
阅读更多...
原始套接字

原始套接字

解析MAC数据包原始套接字-解析MAC数据包 原始套接字.c 套接字类型 原始套接字 1、一种不同于SOCK_STREAM、SOCK_DGRAM的套接字，它实现于系统核心 2、可以接收本机网卡上所有的数据帧（数据包）,对于监听网络流量和分析网络数据很有作用 3、开发人员可发送自己组装的数据包到网…
阅读更多...
http与cJSON练习

http与cJSON练习

http与cJSON练习 /**************************************************************************************************** * weather_test.c * 练习tcp连接，与http协议，调用服务器接口，实现获取特定城市的天气信息…
阅读更多...
多线程实现并发

多线程实现并发

多线程实现并发案例多线程并发服务器 架构 void* thread_fun(void* arg) {while(1){recv()/send()} }scokfd = socket() bind() listen() while(1){accept()//连上就创建线程pthread_create(, ,thread_fun, )pthread_detach() }案例 /* # Multi-process concurrent server…
阅读更多...
利用聚合API平台的API接口，利用HTTP协议向服务器发送请求，并接受服务器的响应，要求利用cJSON库对服务器的响应数据进行解析，并输出到终端

利用聚合API平台的API接口，利用HTTP协议向服务器发送请求，并接受服务器的响应，要求利用cJSON库对服务器的响应数据进行解析，并输出到终端

目录题目分析代码结果 题目利用聚合API平台的API接口，利用HTTP协议向服务器发送请求，并接受服务器的响应，要求利用cJSON库对服务器的响应数据进行解析，并输出到终端 分析1.需从源代码网站GitHub或SourceForge代码网站下载cJSON库及阅读下载的README相关手册如何使用cJSON库…
阅读更多...
[DP] [倍增优化] Luogu P1081 [NOIP2012 提高组] 开车旅行

[DP] [倍增优化] Luogu P1081 [NOIP2012 提高组] 开车旅行

[NOIP2012 提高组] 开车旅行 题目描述 小 \(\text{A}\) 和小 \(\text{B}\) 决定利用假期外出旅行，他们将想去的城市从 $1 $ 到 \(n\) 编号，且编号较小的城市在编号较大的城市的西边，已知各个城市的海拔高度互不相同，记城市 \(i\) 的海拔高度为\(h_i\)，城市 \(i\) 和城市 \…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023