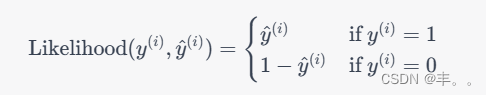PyTorch深度学习实践---笔记

PyTorch深度学习实践---笔记

  • 2.线性模型（Linear Model）
    • 2.exercise
  • 3. 梯度下降算法（Gradient Descent）
    • 3.1梯度下降（Gradient Descent）
    • 3.2 随机梯度下降（Stochastic Gradient Descent）
  • 4. 反向传播（Back Propagation）
  • 5. 用PyTorch实现线性回归
  • 6. 逻辑回归（Logistics Regression）
  • 7. 处理多维特征的输入（Multiple Dimension Input）
  • 8. 加载数据集
  • 9. 多分类问题

2.线性模型（Linear Model）

import numpy as np
import matplotlib.pyplot as pltx_data=[1.0,2.0,3.0]
y_data=[2.0,4.0,6.0]def forward(x):return x*wdef loss(x,y):y_pred=forward(x)return (y_pred-y)*(y_pred-y)w_list=[]
mse_list=[]
for w in np.arange(0.0,4.1,0.1):print('w=',w)l_sum=0for x_val,y_val in zip(x_data,y_data):y_pred_val=forward(x_val)loss_val=loss(x_val,y_val)l_sum+=loss_valprint('\t',x_val,y_val,y_pred_val,loss_val)print('MSE=',l_sum/3)w_list.append(w)mse_list.append(l_sum/3)plt.plot(w_list,mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()

在这里插入图片描述

Exercise：
在这里插入图片描述

[Link](The mplot3d toolkit — Matplotlib 3.7.1 documentation)
[docs](numpy.meshgrid — NumPy v1.25 Manual)

2.exercise

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib notebookx_data=[1.0,2.0,3.0]
y_data=[3.0,5.0,7.0]def forward(x):return x*w+bdef loss(x,y):y_pred=forward(x)return (y_pred-y)*(y_pred-y)w_list=[]
mse_list=[]
b_list=[]
for w in np.arange(0.0,3.1,0.1):for b in np.arange(-1,1.1,0.1):print('w=',w)print('b=',b)l_sum=0for x_val,y_val in zip(x_data,y_data):y_pred_val=forward(x_val)loss_val=loss(x_val,y_val)l_sum+=loss_valprint('\t',x_val,y_val,y_pred_val,loss_val)print('MSE=',l_sum/3)w_list.append(w)b_list.append(b)mse_list.append(l_sum/3)
W=np.array(w_list)
W=np.unique(W)
B=np.array(b_list)
B=np.unique(B)
MSE=np.array(mse_list)W,B=np.meshgrid(W,B)
MSE=MSE.reshape(21,31)
fig=plt.figure()
ax=Axes3D(fig)
ax.plot_surface(W, B, MSE, cmap='rainbow')ax.set_xlabel('W', color='b')
ax.set_ylabel('B', color='g')
ax.set_zlabel('MSE', color='r')
plt.show()

在这里插入图片描述

3. 梯度下降算法（Gradient Descent）

3.1梯度下降（Gradient Descent）

import matplotlib.pyplot as plt  x_data = [1.0, 2.0, 3.0]  
y_data = [2.0, 4.0, 6.0]  w = 1.0  def forward(x):  return x * w  def cost(xs, ys):  cost = 0  for x, y in zip(xs, ys):  y_pred = forward(x)  cost += (y_pred - y) ** 2  return cost / len(xs)  def gradient(xs, ys):  grad = 0  for x, y in zip(xs, ys):  grad += 2 * x * (x * w - y)  return grad / len(xs)  print('Predict(before training)', 4, forward(4))  
cost_list = []  
epoch_list = []  
for epoch in range(100):  cost_val = cost(x_data, y_data)  grad_val = gradient(x_data, y_data)  w -= 0.01 * grad_val  cost_list.append(cost_val)  epoch_list.append(epoch)  print('Epoch:', epoch, 'w=', w, 'loss', cost_val)  
print('Predict(after training)', 4, forward(4))  plt.plot(epoch_list, cost_list)  
plt.xlabel('Epoch')  
plt.ylabel('MSE')  
plt.show()

在这里插入图片描述

3.2 随机梯度下降（Stochastic Gradient Descent）

import matplotlib.pyplot as plt  x_data = [1.0, 2.0, 3.0]  
y_data = [2.0, 4.0, 6.0]  w = 1.0  def forward(x):  return x * w  def loss(x, y):  y_pred = forward(x)  return (y_pred - y) ** 2  def gradient(x, y):  return 2 * x * (x * w - y)  print('Predict(before training)', 4, forward(4))  
loss_list = []  
epoch_list = []  
for epoch in range(100):  for x, y in zip(x_data, y_data):  grad = gradient(x, y)  w -= 0.01 * grad  print("\tgrad:", x, y, grad)  l = loss(x, y)  print("progress:", epoch, "w=", w, "loss=", l)  epoch_list.append(epoch)  loss_list.append(l)  
print('Predict(after training)', 4, forward(4))  plt.plot(epoch_list, loss_list)  
plt.xlabel('Epoch')  
plt.ylabel('Loss')  
plt.show()

在这里插入图片描述

4. 反向传播（Back Propagation）

在这里插入图片描述

Example 1:
在这里插入图片描述

在这里插入图片描述

Exercise 4-1：Answer=-8
在这里插入图片描述

Exercise 4-2 Answer.1=2，Answer.2=2

import torch
from matplotlib import pyplot as plt
x_data=[1.0,2.0,3.0]
y_data=[2.0,4.0,6.0]w=torch.Tensor([1.0])
w.requires_grad=Truedef forward(x):return x*wdef loss(x,y):y_pred=forward(x)return (y_pred-y)**2print("predict (before training)",4,forward(4).item)epoch_list=[]
MSE_list=[]
for epoch in range(100):epoch_list.append(epoch)for x,y in zip(x_data,y_data):l=loss(x,y)l.backward()print('\tgrad:',x,y,w.grad.item())w.data=w.data-0.01*w.grad.dataw.grad.data.zero_()print("progress:",epoch,l.item())MSE_list.append(l.item())
print("prdict (after training)",4,forward(4).item())plt.plot(epoch_list,MSE_list)
plt.xlabel('Epoch')  
plt.ylabel('Loss')
plt.set_tittle("PyTorch")
plt.show()

在这里插入图片描述
在这里插入图片描述

Answer.1：
∂ L o s s ∂ w 1 = 2 ∗ ( w 1 ∗ x 2 + w 2 ∗ x + b − y ) ∗ x 2 \frac{\partial Loss}{\partial w_1}=2*(w_1*x^2+w_2*x+b-y)*x^2 ∂w1​∂Loss​=2∗(w1​∗x2+w2​∗x+b−y)∗x2

Answer.2：
∂ L o s s ∂ w 2 = 2 ∗ ( w 1 ∗ x 2 + w 2 ∗ x + b − y ) ∗ x \frac {\partial Loss}{\partial w_2}=2*(w_1*x^2+w_2*x+b-y)*x ∂w2​∂Loss​=2∗(w1​∗x2+w2​∗x+b−y)∗x

Answer.3：
∂ L o s s ∂ b = 2 ∗ ( w 1 ∗ x 2 + w 2 ∗ x + b − y ) \frac {\partial Loss}{\partial b}=2*(w_1*x^2+w_2*x+b-y) ∂b∂Loss​=2∗(w1​∗x2+w2​∗x+b−y)

在这里插入图片描述

import torch
from matplotlib import pyplot as plt
x_data=[1.0,2.0,3.0]
y_data=[2.0,4.0,6.0]w_1=torch.Tensor([1.0])
w_1.requires_grad=True
w_2=torch.Tensor([2.0])
w_2.requires_grad=True
b=torch.Tensor([3.0])
b.requires_grad=Truedef forward(x):return w_1*(x**2)+w_2*x+bdef loss(x,y):y_pred=forward(x)return (y_pred-y)**2print("predict (before training)",4,forward(4).item)epoch_list=[]
MSE_list=[]
for epoch in range(100):epoch_list.append(epoch)for x,y in zip(x_data,y_data):l=loss(x,y)l.backward()print('\tgrad:','X:',x,'Y:',y,w_1.grad.item(),w_2.grad.item(),b.grad.item())w_1.data=w_1.data-0.01*w_1.grad.dataw_2.data=w_2.data-0.01*w_2.grad.datab.data=b.data-0.01*b.grad.dataw_1.grad.data.zero_()w_2.grad.data.zero_()b.grad.data.zero_()print("progress:",epoch,l.item())MSE_list.append(l.item())
print("prdict (after training)",4,forward(4).item(),'w_1=',w_1.item(),'w_2=',w_2.item(),'b=',b.data.item())plt.plot(epoch_list,MSE_list)
plt.xlabel('Epoch')  
plt.ylabel('Loss')
plt.title("PyTorch")
plt.show()

在这里插入图片描述

5. 用PyTorch实现线性回归

在这里插入图片描述

前馈->反馈->更新
前馈算损失，反馈算梯度，然后更新，反反复复
在这里插入图片描述

import torch
x_data=torch.Tensor([[1.0],[2.0],[3.0]])
y_data=torch.Tensor([[2.0],[4.0],[6.0]])class LinearModel(torch.nn.Module):#LinearModel相当于是继承torch.nn.Module的子类def __init__(self):#Python中类的初始化都是__init__()super(LinearModel,self).__init__()#继承父类的__init__方法,在__init__初始化方法后还想继承父类的__init__(),就在子类中使用super（）函数self.linear=torch.nn.Linear(1,1)#定义子类的linear属性def forward(self,x):y_pred=self.linear(x)#调用子类的linear属性return y_pred
model=LinearModel()#创建类LinearModel的实例criterion=torch.nn.MSELoss(reduction='sum')#损失函数
optimizer=torch.optim.SGD(model.parameters(),lr=0.01)#优化器for epoch in range(1000):#训练迭代y_pred=model(x_data)loss=criterion(y_pred,y_data)print(epoch,loss.item())optimizer.zero_grad()#梯度清零loss.backward()#反向传播optimizer.step()#计算梯度，梯度更新print('w =',model.linear.weight.item())
print('b =',model.linear.bias.item())x_test=torch.Tensor([4.0])
y_test=model(x_test)
print('y_pred =',y_test.data)

这篇文章可以帮助理解LinearModel的写法

python类中super()_wanghua609的博客-CSDN博客

6. 逻辑回归（Logistics Regression）

逻辑回归主要用于分类问题，线性回归的输出值是连续空间
Classification Problem

类别之间没有大小关系

分类问题的输出是一个概率问题，为Ⅰ类的概率是多少，为Ⅱ类的概率是多少…
根据概率值的最大值判断所属类别。
在这里插入图片描述

实际上计算的就是 y_hat=1 的概率。
要将输出值映射到【0，1】，因为概率值是在【0，1】的。
Sigmoid函数也是一种饱和函数（输入值x大于某个值后，输出值y基本不变）。
sigmoid函数中最出名的函数就是Logistics函数，因此大多数书籍资料中将Logistics函数成为sigmoid函数。
σ（）就是sigmoid函数。
在这里插入图片描述

计算分布之间的差异。
这个用于二分类的函数，叫做BCE函数。（CE：cross-entropy）
在这里插入图片描述

在这里插入图片描述

#torch.nn.Functional.sigmoid() use torch.sigmoid() instead.
import torch
import numpy as np
import matplotlib.pyplot as pltx_data=torch.Tensor([[1.0],[2.0],[3.0]])
y_data=torch.Tensor([[0],[0],[1]])class LogisticRegressionModel(torch.nn.Module):def __init__(self):super(LogisticRegressionModel,self).__init__()self.linear=torch.nn.Linear(1,1)def forward(self,x):y_pred=torch.sigmoid(self.linear(x))return y_predmodel=LogisticRegressionModel()criterion=torch.nn.BCELoss(reduction='sum')
#size_average=True
#size_average and reduce args will be deprecated, 
#please use reduction='mean' instead.
optimizer=torch.optim.SGD(model.parameters(),lr=0.01)for epoch in range(1000):y_pred=model(x_data)loss=criterion(y_pred,y_data)print(epoch,loss.item())optimizer.zero_grad()loss.backward()optimizer.step()x=np.linspace(0,10,200)
x_t=torch.Tensor(x).view((200,1))
y_t=model(x_t)
y=y_t.data.numpy()
plt.plot(x,y)
plt.plot([0,10],[0.5,0.5],c='r')
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid()
plt.show()

在这里插入图片描述

7. 处理多维特征的输入（Multiple Dimension Input）

输入值有多个特征
每一行成为Record， 每一列叫做Feature（特征/字段），结构化的数据。
在这里插入图片描述

每一个特征值都要与一个权重相乘，x看成一个向量，乘上w1到w8，标量转置相乘做内积。
σ就是sigmoid函数。
计算转化成向量化的运算，然后通过并行计算，通过GPU的能力，提高运算速度。
矩阵可以看作是空间变换的函数。
在这里插入图片描述
在这里插入图片描述

从8个特征（8维）学到6个特征（6维）再到4个特征，最后到1个特征。
当然也可以直接从8个特征学到1个特征

import numpy as np
import torch
import matplotlib.pyplot as pltxy = np.loadtxt('diabetes.csv', delimiter=',', dtype=np.float32)
x_data = torch.from_numpy(xy[:, :-1]) 
y_data = torch.from_numpy(xy[:, [-1]]) class Model(torch.nn.Module):def __init__(self):super(Model, self).__init__()self.linear1 = torch.nn.Linear(8, 6)self.linear2 = torch.nn.Linear(6, 4)self.linear3 = torch.nn.Linear(4, 1)self.sigmoid = torch.nn.Sigmoid() def forward(self, x):x = self.sigmoid(self.linear1(x))x = self.sigmoid(self.linear2(x))x = self.sigmoid(self.linear3(x)) return xmodel = Model()criterion = torch.nn.BCELoss(reduction='mean')  
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)epoch_list = []
loss_list = []for epoch in range(100000):y_pred = model(x_data)loss = criterion(y_pred, y_data)print(epoch, loss.item())epoch_list.append(epoch)loss_list.append(loss.item())optimizer.zero_grad()loss.backward()optimizer.step()plt.plot(epoch_list, loss_list)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()

在这里插入图片描述

8. 加载数据集

Dataset主要用于构建数据集，支持索引（利用下标）
Dataloader主要用于Mini-Batch
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

笔记来源：《PyTorch深度学习实践》完结合集

9. 多分类问题

输出时，每一个输出代表每种标签的概率。属于1的概率是多少，属于2的概率是多少，等等。各个输出值大于0，且值得的合等于1。

本笔记来自：【《PyTorch深度学习实践》完结合集】 https://www.bilibili.com/video/BV1Y7411d7Ys/?share_source=copy_web&vd_source=292129053a8880be150381f42c6b50c4

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/72700.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Java虚拟机（JVM）：虚拟机栈溢出

Java虚拟机（JVM）：虚拟机栈溢出

一、概念 Java虚拟机栈溢出（Java Virtual Machine Stack Overflow）是指在Java程序中，当线程调用的方法层级过深，导致栈空间溢出的情况。 Java虚拟机栈是每个线程私有的，用于存储方法的调用和局部变量的内存空间。每当…
阅读更多...
ARFoundation避坑记录

ARFoundation避坑记录

网上很多人说这个要改成可选的，否则如果没有安装arcore就会自动弹窗，但是如果关闭了，确实不会弹窗了，但是检测设备的代码也不能完美执行了，如果设备安装了arcore还好，如果没有安装测无法检测。 如果不想有…
阅读更多...
Spark第三课

Spark第三课

1.分区规则 1.分区规则 shuffle 1.打乱顺序 2.重新组合 1.分区的规则 默认与MapReduce的规则一致,都是按照哈希值取余进行分配. 一个分区可以多个组,一个组的数据必须一个分区 2. 分组的分区导致数据倾斜怎么解决? 扩容 让分区变多修改分区规则 3.HashMap扩容为什么必须…
阅读更多...
数据结构——单链表的实现(c语言版）

数据结构——单链表的实现(c语言版）

前言 单链表作为顺序表的一种，了解并且熟悉它的结构对于我们学习更加复杂的数据结构是有一定意义的。虽然单链表有一定的缺陷，但是单链表也有它存在的价值， 它也是作为其他数据结构的一部分出现的，比如在图，哈希表中。…
阅读更多...
vue使用jsplumb 流程图

vue使用jsplumb 流程图

安装jsPlumb库&#xff1a;在Vue项目中使用npm或yarn安装jsPlumb库。 npm install jsplumb 创建一个Vue组件&#xff1a;创建一个Vue组件来容纳jsPlumb的功能和呈现。 <template><div style"margin: 20px"><div style"margin: 20px">&l…
阅读更多...
Windows CMD 关闭，启动程序

Windows CMD 关闭，启动程序

Windows CMD 关闭&#xff0c;启动程序 1. Windows 通过 CMD 命令行关闭程序 示例&#xff1a;通过 taskkill 命令关闭 QQ 管家&#xff0c;但是这里有个问题&#xff0c;使用命令行关闭 QQ 管家时&#xff0c;会提示“错误: 无法终止 PID 1400 (属于 PID 22116 子进程)的进程…
阅读更多...
postgresql 分类排名

postgresql 分类排名

postgresql 分类排名 排名窗口函数示例CUME_DIST 和 NTILE 排名窗口函数 排名窗口函数用于对数据进行分组排名。常见的排名窗口函数包括&#xff1a; • ROW_NUMBER&#xff0c;为分区中的每行数据分配一个序列号&#xff0c;序列号从 1 开始分配。 • RANK&#xff0c;计算每…
阅读更多...
Ribbon 源码分析

Ribbon 源码分析

Ribbon 源码分析 Ribbon Debug 分析 断点 LoadBalancerInterceptor LoadBalancerInterceptor 实现了 ClientHttpRequestInterceptor 接口&#xff0c;重写了其中的 intercept 方法&#xff0c;用来拦截请求&#xff1b; 获取原始的 uri 和 服务名&#xff0c;调用 LoadBalanc…
阅读更多...
Java IO流（一）IO基础

Java IO流（一）IO基础

概述 IO流本质 I/O表示Input/Output,即数据传输过程中的输入/输出,并且输入和输出都是相对于内存来讲Java IO(输入/输出)流是Java用于处理数据读取和写入的关键组件常见的I|O介质包括 文件(输入|输出)网络(输入|输出)键盘(输出)显示器(输出)使用场景 文件拷贝&#xff08;File&…
阅读更多...
网络通信原理TCP的四次断开连接（第四十九课）

网络通信原理TCP的四次断开连接（第四十九课）

FIN：发端完成发送任务标识。用来释放一个连接。FIN=1表明此报文段的发送端的数据已经发送完毕，并要求释放连接。 SEQ：序号字段。 TCP链接中传输的数据流中每个字节都编上一个序号。序号字段的值指的是本报文段所发送的数据的第一个字节的序号。 序列号为X ACK :确认号 。 …
阅读更多...
【快应用】快应用广告学习之激励视频广告

【快应用】快应用广告学习之激励视频广告

【关键词】 快应用、激励视频广告、广告接入 【介绍】 一、关于激励视频广告 定义&#xff1a;用户通过观看完整的视频广告&#xff0c;获得应用内相关的奖励。适用场景&#xff1a;游戏/快游戏的通关、继续机会、道具获取、积分等场景中&#xff0c;阅读、影音等应用的权益体系…
阅读更多...
神经网络基础-神经网络补充概念-14-逻辑回归中损失函数的解释

神经网络基础-神经网络补充概念-14-逻辑回归中损失函数的解释

概念 逻辑回归损失函数是用来衡量逻辑回归模型预测与实际观测之间差异的函数。它的目标是找到一组模型参数&#xff0c;使得预测结果尽可能接近实际观测。 理解 在逻辑回归中&#xff0c;常用的损失函数是对数似然损失&#xff08;Log-Likelihood Loss&#xff09;&#xff…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023