概念
逻辑回归损失函数是用来衡量逻辑回归模型预测与实际观测之间差异的函数。它的目标是找到一组模型参数,使得预测结果尽可能接近实际观测。
理解
在逻辑回归中,常用的损失函数是对数似然损失(Log-Likelihood Loss),也称为交叉熵损失(Cross-Entropy Loss)。它在分类问题中非常常见,特别适用于二分类问题。
公式
假设我们有一组训练样本 ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , … , ( x ( m ) , y ( m ) ) (x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), \ldots, (x^{(m)}, y^{(m)}) (x(1),y(1)),(x(2),y(2)),…,(x(m),y(m)),其中 x ( i ) x^{(i)} x(i) 是输入特征, y ( i ) y^{(i)} y(i) 是对应的实际标签(0 或 1)。模型的预测结果为 y ^ ( i ) \hat{y}^{(i)} y^(i),它是由逻辑回归函数转换得到的: y ^ ( i ) = h θ ( x ( i ) ) = 1 1 + e − θ T x ( i ) \hat{y}^{(i)} = h_\theta(x^{(i)}) = \frac{1}{1 + e^{-\theta^T x^{(i)}}} y^(i)=hθ(x(i))=1+e−θTx(i)1。
对于每个样本,我们可以定义一个对数似然函数:
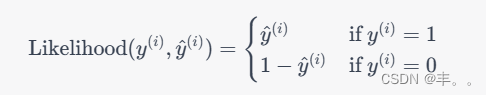
其中 m m m 是样本数量。
这个损失函数的意义是,当模型的预测结果与实际标签一致时,对数似然损失趋近于0。当模型的预测与实际不一致时,损失会逐渐增加。因此,优化模型的参数就是通过最小化这个损失函数,使得模型的预测结果尽可能接近实际标签。
逻辑回归损失函数的优化通常使用梯度下降等优化算法。通过迭代更新模型参数,最终使得损失函数达到最小值,从而得到能够对数据进行合理分类的逻辑回归模型。
代码实现
import numpy as np
from sklearn.model_selection import train_test_split# 生成模拟数据
np.random.seed(42)
m = 100
n = 2
X = np.random.randn(m, n)
X = np.hstack((np.ones((m, 1)), X))
theta_true = np.array([1, 2, 3])
y = (X.dot(theta_true) + np.random.randn(m) * 0.2) > 0# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 初始化模型参数
theta = np.zeros(X_train.shape[1])# 定义sigmoid函数
def sigmoid(z):return 1 / (1 + np.exp(-z))# 定义损失函数
def compute_loss(X, y, theta):m = len(y)h = sigmoid(X.dot(theta))loss = (-1/m) * np.sum(y * np.log(h) + (1 - y) * np.log(1 - h))return loss# 定义梯度计算函数
def compute_gradient(X, y, theta):m = len(y)h = sigmoid(X.dot(theta))gradient = X.T.dot(h - y) / mreturn gradient# 执行梯度下降
learning_rate = 0.01
num_iterations = 1000for _ in range(num_iterations):gradient = compute_gradient(X_train, y_train, theta)theta -= learning_rate * gradient# 在测试集上计算损失
test_loss = compute_loss(X_test, y_test, theta)
print("测试集上的损失:", test_loss)