奇异值分解(Singular Value Decomposition)是线性代数中一种重要的矩阵分解,具有压缩矩阵信息的作用
- 一、奇异值分解的理论介绍
- 1.奇异值分解的例子
- 2.U的计算
- 3.V的计算
- 4.Σ的计算
- 5.利用SVD对数据进行"降维"
- (1)对U与V进行分块,得到分块矩阵
- (2)去除奇异值后得到压缩后的矩阵
- (3)保留原矩阵的特征比例
- 二、Matlab进行奇异值分解
- 1.[U,S,V] = svd(A)
- (1)矩阵分解
- (2)矩阵重构
- 2.编写可直接进行奇异值分解的函数————mysvd
- 1.[U,S,V] = svd(A)
一、奇异值分解的理论介绍
1.奇异值分解的例子
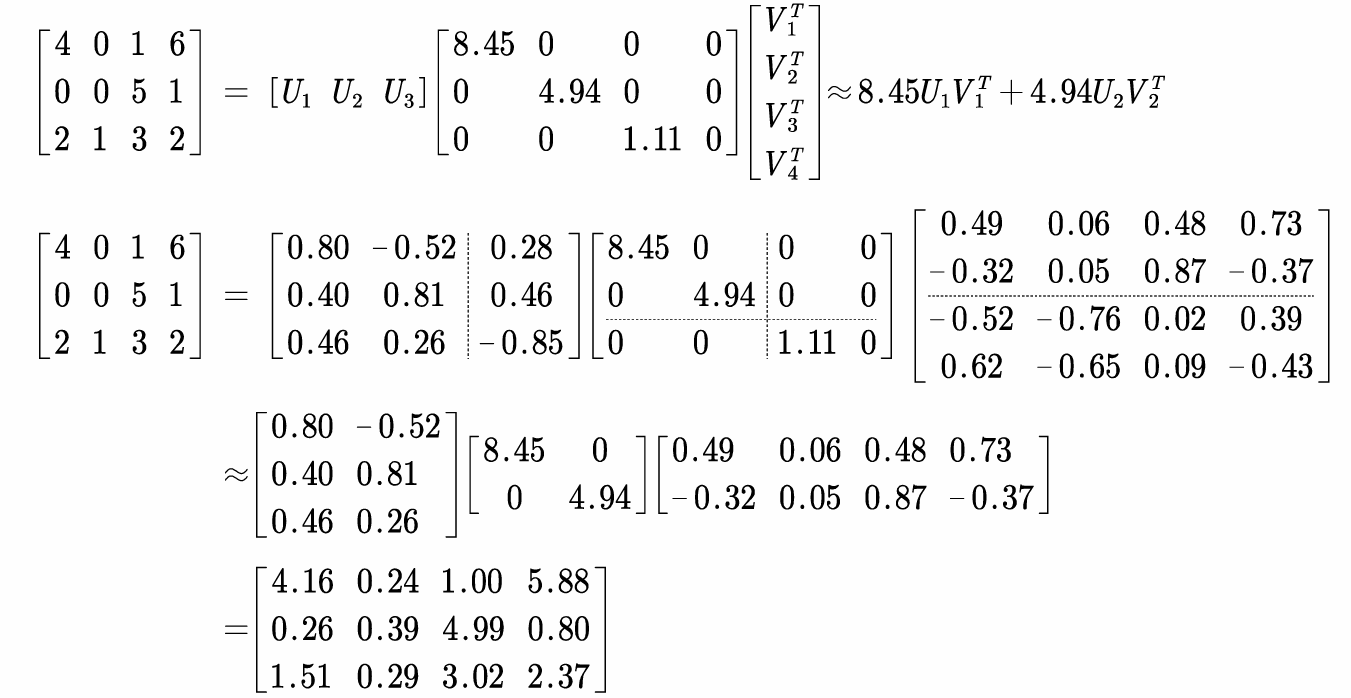
所谓奇异值分解,就是把矩阵A分解成三个矩阵的乘积,其中中间的矩阵只有主对角线有元素,上面的元素就是奇异值

2.U的计算
对A乘以A的转置相似对角化,得到的UΛU'。

3.V的计算
对A的转置乘以A相似对角化,得到的VΛV'。

4.Σ的计算
A*A'与A'A的特征值相同,将其特征值开方就可以得到我们的奇异值

5.利用SVD对数据进行"降维"
这⾥所说的降维,实际上是使得矩阵的秩减小,矩阵大小并未改变。
(1)对U与V进行分块,得到分块矩阵
此处我们的第三项奇异值占比过小,所以我们想去除第三项

(2)去除奇异值后得到压缩后的矩阵
由于第三项奇异值被去除,因此我们对Σ的处理就是保留前两行,因此U也只保留前两列,V只保留前两行。处理之后得到了我们压缩后的矩阵
(3)保留原矩阵的特征比例
通过奇异值分解,我们得到了保留原矩阵93%信息的新矩阵

二、Matlab进行奇异值分解
1.[U,S,V] = svd(A)
(1)矩阵分解
在matlab中有自带的函数可以帮助我们进行奇异值分解。返回的第一个参数为U,第二个参数为Σ,第三个参数为V。输入的参数为需要进行奇异值分解的矩阵A
[U,S,V] = svd(A)
效果如图所示

(2)矩阵重构
经过观察,我们只想保留前两项奇异值。Σ的行数从3行变成了2行,因此我们要重构矩阵,就只保留U的前两个列。Σ的列数从4列变成了两列,因此V也只保留前两行
U(:,1:2)*S(1:2,1:2)*V(:,1:2)' 注意:此处的V是经过转置的

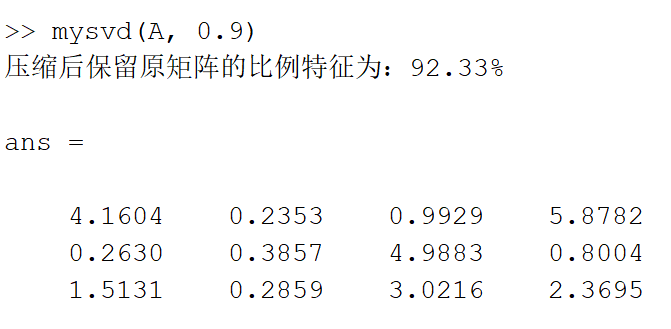
2.编写可直接进行奇异值分解的函数————mysvd
[compress_A] = mysvd(A, ratio)这是我们自己编写的函数,这里所输出的参数就是经过压缩过后的A。需要输入的一个参数为需要处理的矩阵A,第二个参数为最少需要保存的比例
此函数的编写并不复杂,也调用了matlab的函数svd,通过建立一个循环,当保存的比例大于所给的ration时就退出循环,然后输出经过压缩的矩阵