个人赛补题

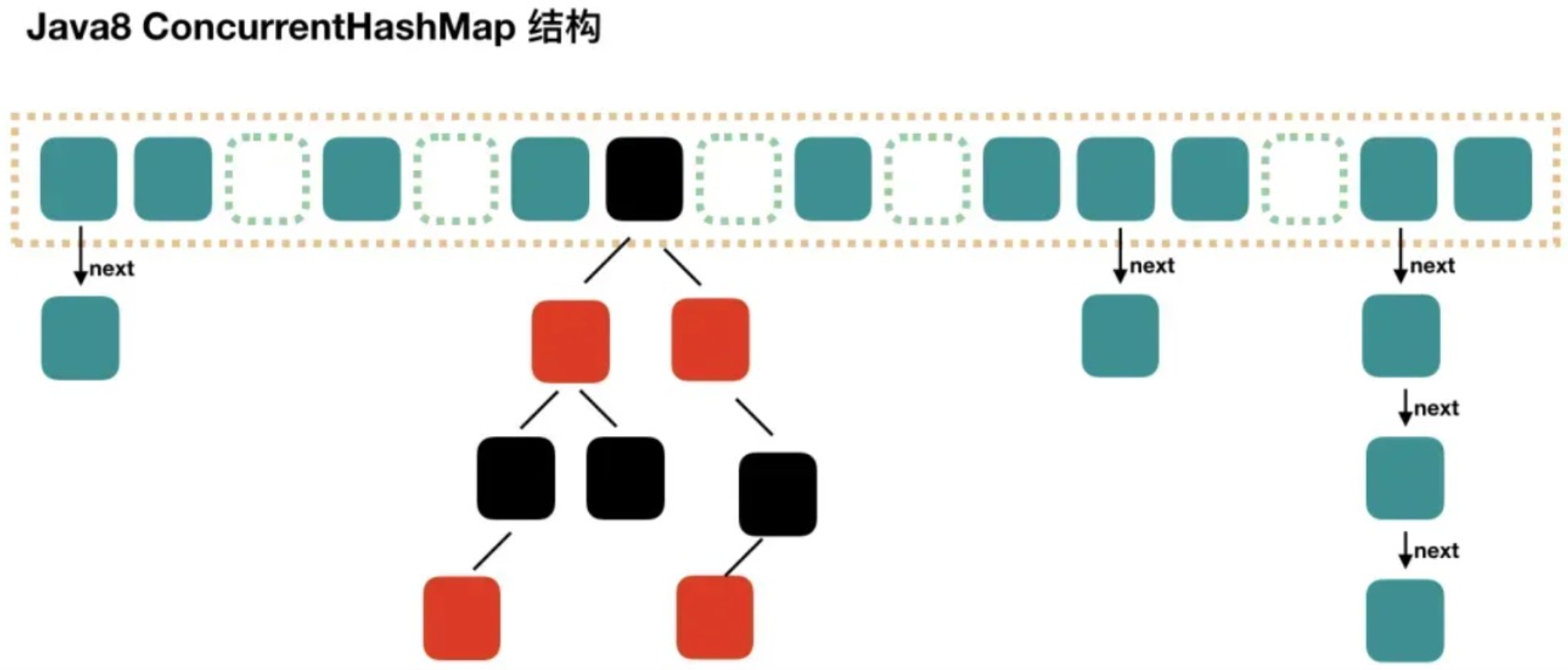
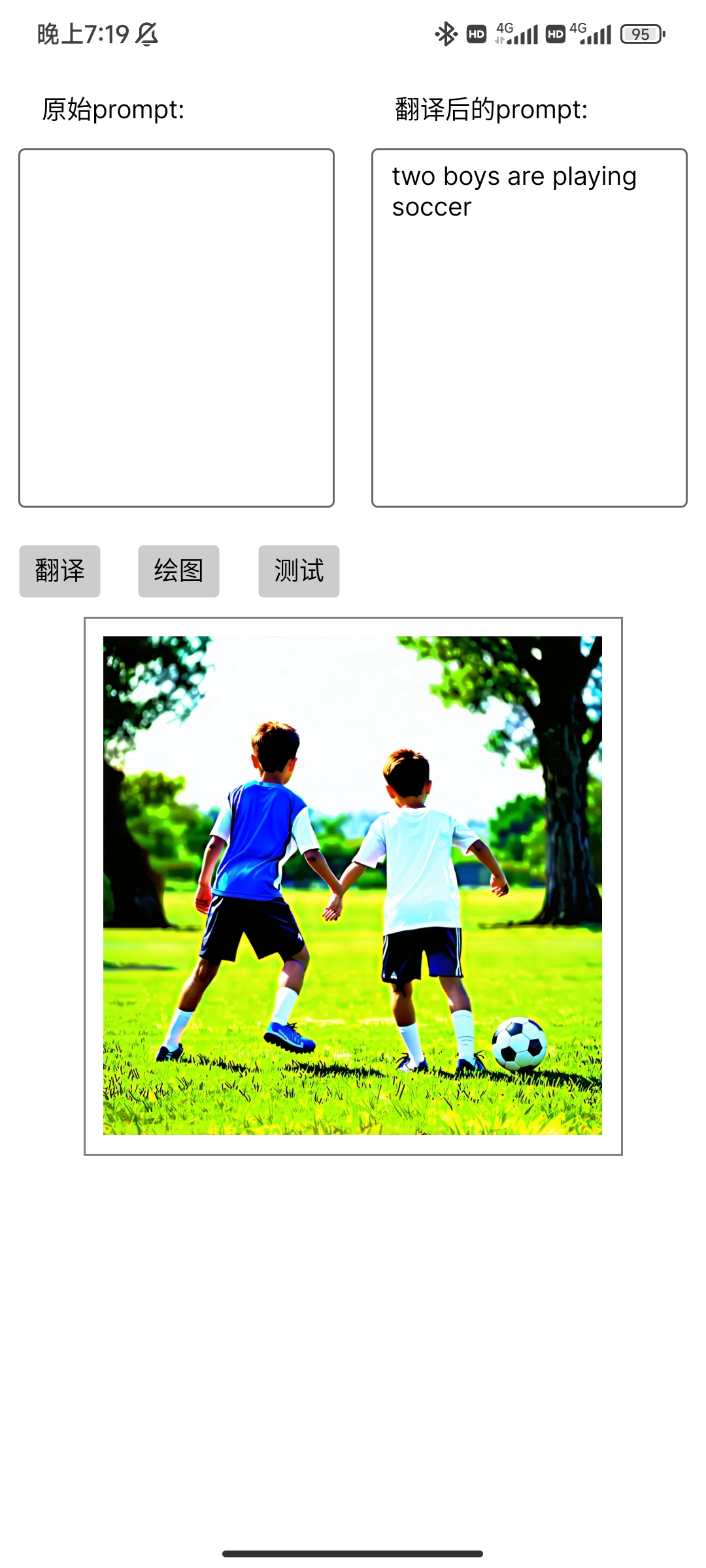
round 1

范围很小用暴力+贪心，左右枚举，先拿再放。尽量放小的所以需要排下序

include

include "map"

include "algorithm"

include "cmath"

include "vector"

include "set"

include "queue"

define int long long

using namespace std;
void solve(){
int n,k;
cin>>n>>k;
int s[n+5];
for(int i=1;i<=n;i++)
cin>>s[i];
int ans=-1e9;
for(int i=0;i<=min(n,k);i++){
for(int j=0;j<=min(n,k)-i;j++){
vector vt;
int sd=0;
for(int q=1;q<=i;q++) {
vt.emplace_back(s[q]);
sd+=s[q];
}
for(int q=1;q<=j;q++) {
vt.emplace_back(s[n - q + 1]);
sd+=s[n-q+1];
}
sort(vt.begin(),vt.end());
for(int q=1;q<=k-i-j&&q<=vt.size();q++){
if(vt[q-1]<0)
sd-=vt[q-1];
else
break;
}
ans=max(ans,sd);
}
}
cout<<ans;
}
signed main()
{
int t=1;
//cin>>t;
while(t--){
solve();
}
}

round 2

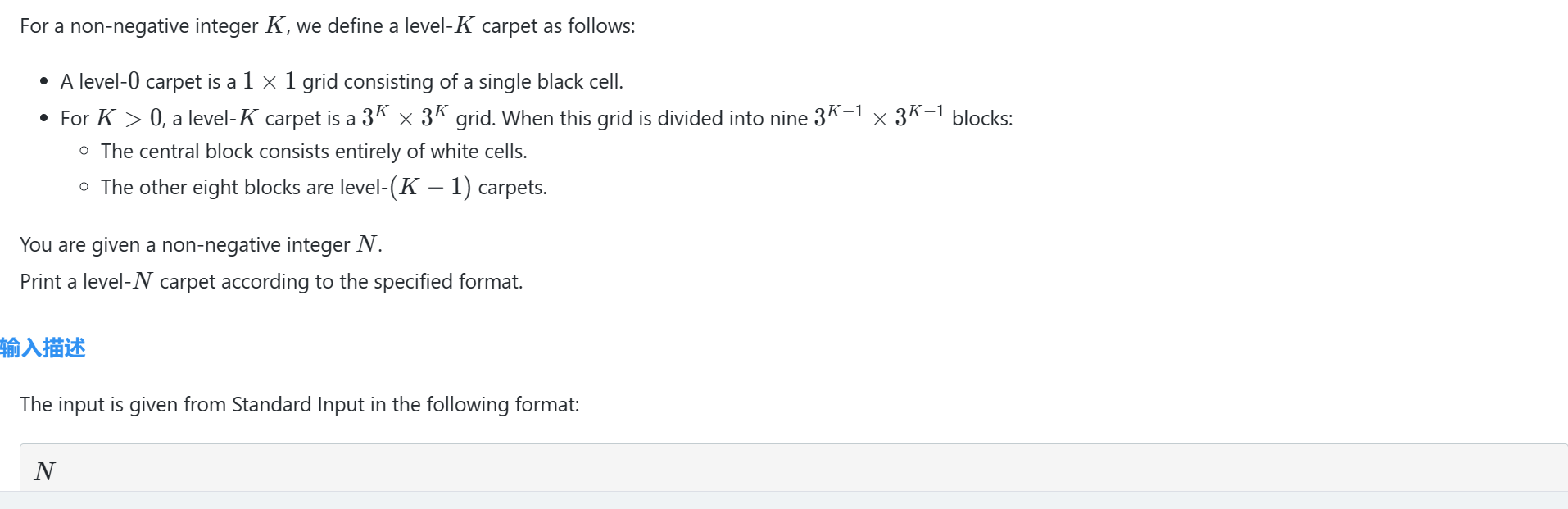
刚开始写这道题因为看到范围比较小，所以打算直接把图形输出，后来逐渐尝试发现根本不行，到6的时候就要输出700多行了。看完题解后发现可以搜索。从8个方向去搜索，其中'.'赋为0，'#'为1.

include<bits/stdc++.h>

using namespace std;
int a[2000][2000];//0:黑,1:白
void dfs(int x,int y,int k){
if(k==0){
a[x][y]=0;
return ;
}
dfs(x,y,k-1);
dfs(x+pow(3,k-1),y,k-1);
dfs(x+pow(3,k-1)2,y,k-1);
dfs(x,y+pow(3,k-1),k-1);
dfs(x,y+pow(3,k-1)2,k-1);
dfs(x+pow(3,k-1),y+pow(3,k-1)2,k-1);
dfs(x+pow(3,k-1)2,y+pow(3,k-1),k-1);
dfs(x+pow(3,k-1)2,y+pow(3,k-1)2,k-1);
for(int i=x+pow(3,k-1);i<x+pow(3,k-1)2;i++){
for(int j=y+pow(3,k-1);j<y+pow(3,k-1)2;j++){
a[i][j]=1;
}
}
}
int main(){
int n;
cin>>n;
dfs(0,0,n);
for(int i=0;i<pow(3,n);i++){
for(int j=0;j<pow(3,n);j++){
if(a[i][j]) cout<<'.';
else cout<<'#';
}
cout<<endl;
}
}

因为节点 到最近黑色节点的最短距离已经是最小值，所以我们把最短距离小于给定距离的节点全部排除。然后判断对于一个节点，是否所有的距离等于给定距离的节点都被排除了。如果是，说明无解，输出 -1，结束程序。若不存在无解，则说明一定有解。把排除成为黑色节点的全部输出为白色节点，否则输出位黑色节点。

include <bits/stdc++.h>

define int long long

using namespace std;
pair<int,int> p1[2005],p2[2005];
map<int,int> ma;
map<int,set> mp;
void solve(){
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int a,b;
cin>>a>>b;
p1[i]={a,b};
mp[a].insert(b);
mp[b].insert(a);
}
int k=1;
cin>>k;
for(int i=1;i<=k;i++){
int a,b;
cin>>a>>b;
p2[i]={a,b};
}
for(int i=1;i<=k;i++){
queue num,cnt;
map<int,int> mo;
num.push(p2[i].first);
cnt.push(0);
while(num.size()!=0){
int x=num.front(),y=cnt.front();
num.pop(),cnt.pop();
if(mo[x]||yp2[i].second) continue;
mo[x]=1,ma[x]=1;
for(auto x:mp[x]){
num.push(x);
cnt.push(y+1);
}
}
}
for(int i=1;i<=k;i++){
queue num,cnt;
int o=0;
bool f=false;
map<int,int> mo;
num.push(p2[i].first);
cnt.push(0);
while(num.size()!=0) {
int x=num.front(),y=cnt.front();
num.pop(),cnt.pop();
if(mo[x]) continue;
if(yp2[i].second){
if(!ma[x]){
f=true;
break;
}
continue;
}
mo[x]=1,ma[x]=1;
for(auto x:mp[x]){
num.push(x);
cnt.push(y+1);
}
}
if(f==false){
cout<<"No\n";
return;
}
}
cout<<"Yes\n";
for(int i=1;i<=n;i++){
if(ma[i]){
cout<<'0';
}
else
cout<<'1';
}
}
signed main(){
int t=1;
//cin>>t;
while(t--)
solve();
}
Round 3

这道题是一道dp，但是这个题目有一点错误，它并没有说多组输入，愣是给我交了十几发才发现。这个就是二维dp，dp[i][j]其中i表示前i个数字中有j对的最小代价是什么。有两种转移方式。一个是加上最后的i，一个是不加最后的i也就是dp[i-1][j]。二者取最小。

include

include "algorithm"

include "cstring"

define inf 0x3f3f3f3f

using namespace std;
int dp[2005][2005];
int s[20005];
int main(){
int n,k;
while(cin>>n>>k){
memset(s,0,sizeof(s));
memset(dp,inf,sizeof(dp));
dp[0][0]=0;
for(int i=1;i<=n;i++){
cin>>s[i];
dp[i][0]=0;
}
sort(s+1,s+n+1);
for(int i=2;i<=n;i++){
for(int j=1;j<=k;j++){
dp[i][j]=min(dp[i-1][j],dp[i-2][j-1]+((s[i]-s[i-1])*(s[i]-s[i-1])));
}
}
cout<<dp[n][k]<<'\n';
}
}