点分治

介绍

点分治, 作为一种统计带权树简单路径长度的暴力分治算法, 其分治方法非常的巧妙, 可以将暴力的 \(O(n^2)\) 优化到 \(O(nlogn)\)

先看问题:
在一个带权树上, 统计两个点的简单路径长度不超过 \(k\) 的路径个数

这就是 模板题1 POJ1741
首先还是考虑如何使用暴力求出, 很明显的我们直接对树上的每个点做一遍 \(dfs\) 即可, 这样的时间复杂度是 \(O(n^2)\)
太慢了, 有没有什么方法可以进行优化?

我们考虑树上的一个点 \(t\), 那么对于该点来说, 可以把问题简单的分为两大类, 第一类是经过点 \(t\) 的路径的点, 另一类是不经过该点的路径的点.

关于第二大类, 也就是不经过 \(t\) 的点, 我们考虑把该点删除之后, 原图会变成若干个无根树, 然后其点一定会在这些子树的某个路径上, 我们可以递归求出

然后考虑计算第一类问题: 可以对该点进行一遍 \(dfs\), 求出每个点到其的距离, 然后对这些距离排序, 这样我们就有了一个有序的距离数组, 那么使用双指针就可以求出此时符合条件的所有可能

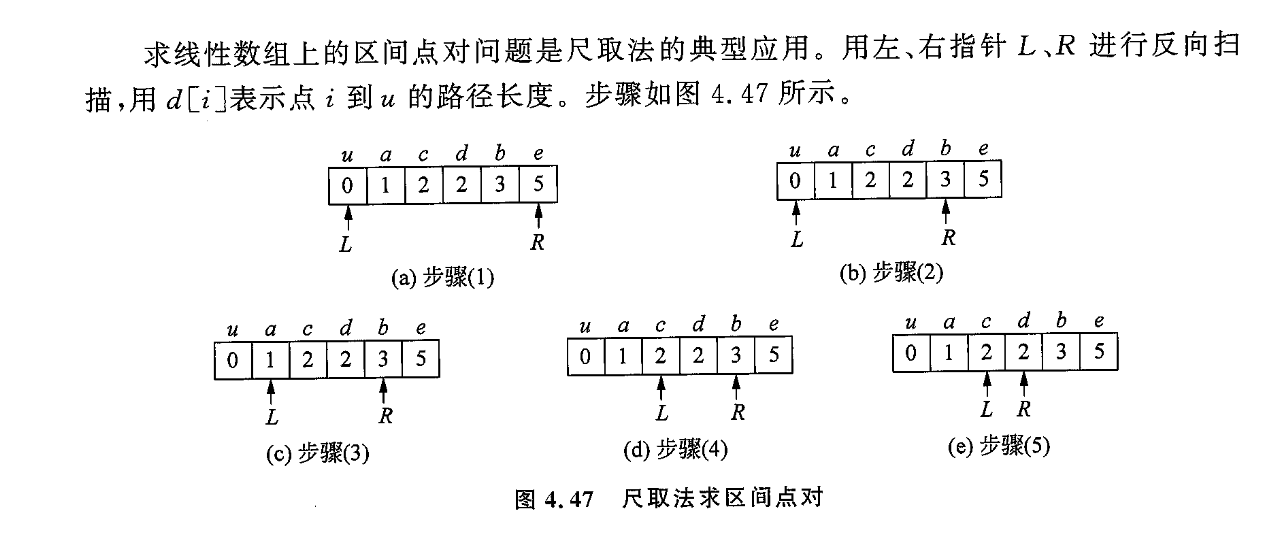
然后你会发现, 这些路径中很明显有一些是有问题的, 举例子来说, 当前的 \(k = 7\), 此时有这样一种情况:

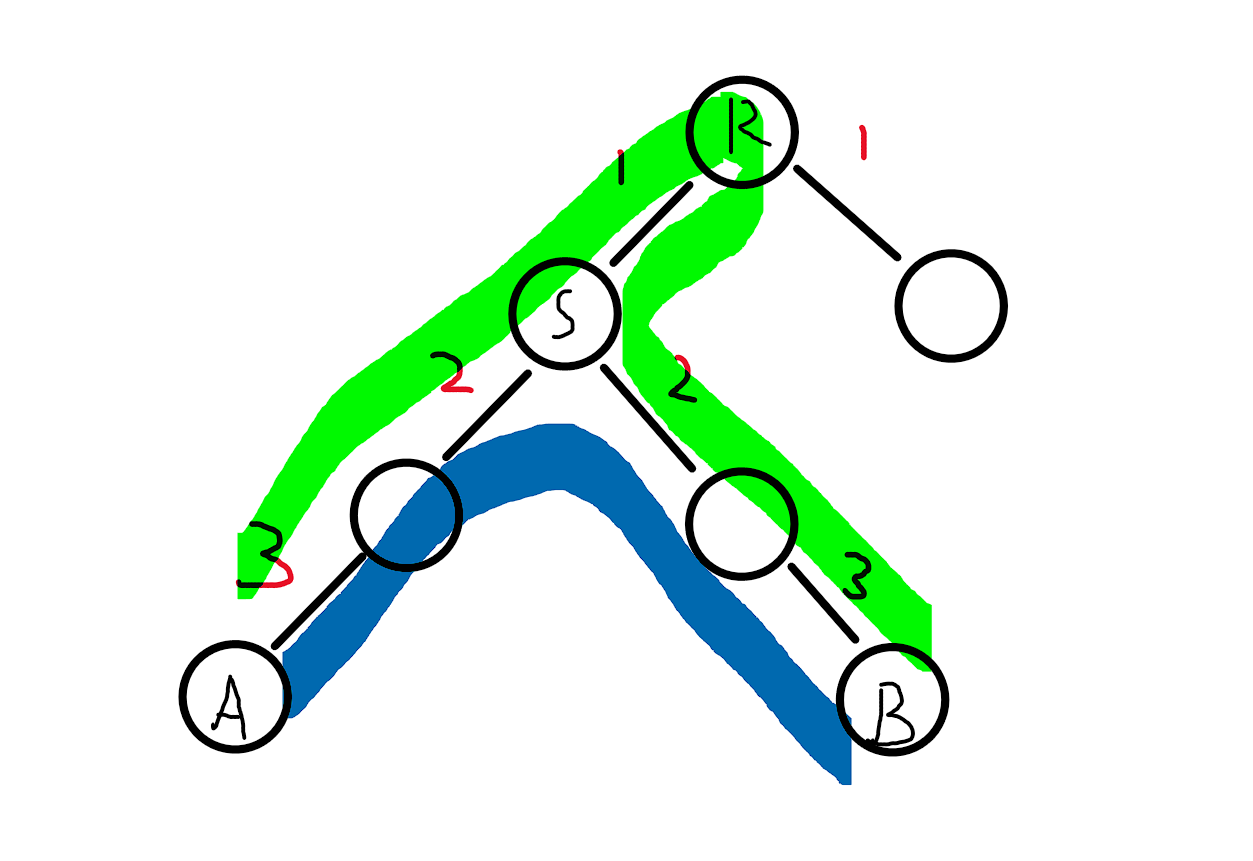
从根节点 \(R\) 到 节点 \(X\), \(Y\) 的距离均为 \(3\), 那么此时这个路径已经被纳入合法路径了, 实则不然, 仔细观察发现这条路径实际上是: \(R → X → R → Y\) 实际的长度是 \(9\), 实际上这样是因为它不是一个简单路径,所以不合法,我们需要去除这个不合法的路径, 从整体上来看, 同一子树内的两个节点组成的路径均不合法(即绿色色路径).

如何去除? 我们考虑从子树入手, 我们直接计算以子节点为根的子树, 我们此时我们有 \(R → S\) 这条边, 也就是说, 我们可以把原来的 \(k\) 变成 \(k + W_\text{R → S}\) (即蓝色路径), 这样我们就可以把这些不合法的路径通通去除了

这样, 我们就在 \(O(nlogn)\) 的时间复杂度内求一个点的合法方案得到了, 接下来

为什么要这样做? 如果我们还是一个点一个点的这样求, 那么还徒增了一个排序, 硬是把复杂度优化到了 \(O(n^2logn)\)
很明显我们肯定不可以再一个一个去求了, 我们在上述方法中提到了一点, 也就是在递归的过程中, 要删去之前求出过的节点, 那么会分裂成若干个无根树, 也就是说, 我们需要尽可能的减少这些树的数量, 以达到最优, 那么此时我们最重要的地方出来了: 重心, 没错, 每次都用重心做根节点, 分裂的子树大小不过超过 \(\frac{n}{2}\),我们只需要 \(logn\) 层即可完成递归!
递归复杂度: \(logn\), 每个点的方案复杂度: \(nlogn\), 总复杂度: \(O(nlog^2n)\)

以下是例题代码:

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e4 + 10, mod = 1e9 + 7;
struct node{int v, w;
};
int n, m, k;
int sz[N], dp[N], dist[N], now, res, Tsize, cnt;
vector<node> g[N];
bool vis[N];
void dfs1(int u, int fa){sz[u] = 1, dp[u] = 0;for(int i = 0; i < g[u].size(); i++){int x = g[u][i].v;if(x == fa || vis[x]) continue;dfs1(x, u);sz[u] += sz[x];dp[u] = max(dp[u], sz[x]);}dp[u] = max(dp[u], Tsize - sz[u]);if(dp[u] < dp[now]) now = u;
}
void dfs2(int u, int fa, int d){dist[++cnt] = d;for(int i = 0; i < g[u].size(); i++){int x = g[u][i].v, w = g[u][i].w;if(x == fa || vis[x]) continue;dfs2(x, u, d + w);}
}
int dfs3(int u, int d){cnt = 0, dfs2(u, 0, d);sort(dist + 1, dist + 1 + cnt);int l = 1, r = cnt, ans = 0;while(l <= r){while(r && dist[l] + dist[r] > k) r--;if(l > r) break;ans += r - l + 1;l++;    }return ans;
}
void dfs(int u){res += dfs3(u, 0);vis[u] = true;for(int i = 0; i < g[u].size(); i++){int x = g[u][i].v, w = g[u][i].w;if(!vis[x]){// 这里实现的步骤是去除子树里面不合法的合并路径res -= dfs3(x, w);// 其实这里加一步这个才是正确的一般点分治, 但是不加也可以, 具体证明: https://liu-cheng-ao.blog.uoj.ac/blog/2969// Tsize = n, dfs1(x, 0);now = 0, Tsize = sz[x], dfs1(x, 0);dfs(now);}}
}
signed main()
{std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);while(cin >> n >> k && n != 0 && k != 0){for(int i = 1; i <= n + 100 ; i++) g[i].clear();memset(vis, false, sizeof vis);for(int i = 1; i < n; i++){int a, b, c; cin >> a >> b >> c;node x = {b, c}, y = {a, c};g[a].push_back(x), g[b].push_back(y);}res = 0;dp[now = 0] = 1e9, Tsize = n, dfs1(1, 0);dfs(now);cout << res - n << '\n';}return 0;
}

例题:

模板点分治1

【模板】点分治 1

题目描述

给定一棵有 \(n\) 个点的树，询问树上距离为 \(k\) 的点对是否存在。
输入格式

第一行两个数 \(n,m\)。

第 \(2\) 到第 \(n\) 行，每行三个整数 \(u, v, w\)，代表树上存在一条连接 \(u\) 和 \(v\) 边权为 \(w\) 的路径。

接下来 \(m\) 行，每行一个整数 \(k\)，代表一次询问。

输出格式

对于每次询问输出一行一个字符串代表答案，存在输出 AYE，否则输出 NAY。

样例 #1

样例输入 #1

2 1
1 2 2
2

样例输出 #1

AYE

提示

数据规模与约定

• 对于 \(30\%\) 的数据，保证 \(n\leq 100\)。
• 对于 \(60\%\) 的数据，保证 \(n\leq 1000\)，\(m\leq 50\) 。
• 对于 \(100\%\) 的数据，保证 \(1 \leq n\leq 10^4\)，\(1 \leq m\leq 100\)，\(1 \leq k \leq 10^7\)，\(1 \leq u, v \leq n\)，\(1 \leq w \leq 10^4\)。

做法:
本题求的是是否存在距离等于 \(k\) 的路径, 那么我们在求答案的时候用二分更为方便, 接下来要注意本题最好不要每次询问都去跑一边, 很可能会 T, 因为算法常数较大, 这里直接统计即可, 复杂度 \(O(mnlog^2n\))
代码:

#include <bits/stdc++.h>
using namespace std;
const int N = 2e4 + 10, mod = 1e9 + 7;
struct node{int u, w;
};
vector<node> g[N];
int sz[N], dp[N], dist[N], wait[N], ok[N];
int now, Tsize, cnt, k, res, n, m;
bool vis[N];
void dfs1(int u, int fa){sz[u] = 1, dp[u] = 0;for(auto it : g[u]){int x = it.u;if(x == fa || vis[x]) continue;dfs1(x, u);sz[u] += sz[x];dp[u] = max(dp[u], sz[x]); }dp[u] = max(dp[u], Tsize - sz[u]);if(dp[u] < dp[now]) now = u;
}
void dfs2(int u, int fa, int d){dist[++cnt] = d;for(auto it : g[u]){int x = it.u, w = it.w;if(x == fa || vis[x]) continue;dfs2(x, u, d + w);}
}
void dfs3(int u, int d, bool f){cnt = 0, dfs2(u, 0, d);sort(dist + 1, dist + 1 + cnt);for(int j = 1; j <= m; j++){for(int i = 1; i < cnt; i++){int x = lower_bound(dist + i + 1, dist + 1 + cnt, wait[j] - dist[i]) - dist;if(x && x <= cnt && dist[x] + dist[i] == wait[j] && x != i){if(f) ok[j]++;else ok[j]--;}}}
}
void dfs(int u){dfs3(u, 0, true), vis[u] = true;for(auto it : g[u]){int x = it.u, w = it.w;if(vis[x]) continue;dfs3(x, w, false);Tsize = n, dfs1(x, 0);now = 0, Tsize = sz[x], dfs1(x, 0);dfs(now);}
}
signed main()
{std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);cin >> n >> m;for(int i = 1; i < n; i++){int a, b, c; cin >> a >> b >> c;g[a].push_back({b, c}), g[b].push_back({a, c});}for(int i = 1; i <= m; i++) cin >> wait[i];dp[now = 0] = 1e9, Tsize = n, dfs1(1, 0);dfs(now);for(int i = 1; i <= m; i++){if(ok[i]) cout << "AYE" << '\n';else cout << "NAY" << '\n';}return 0;
}