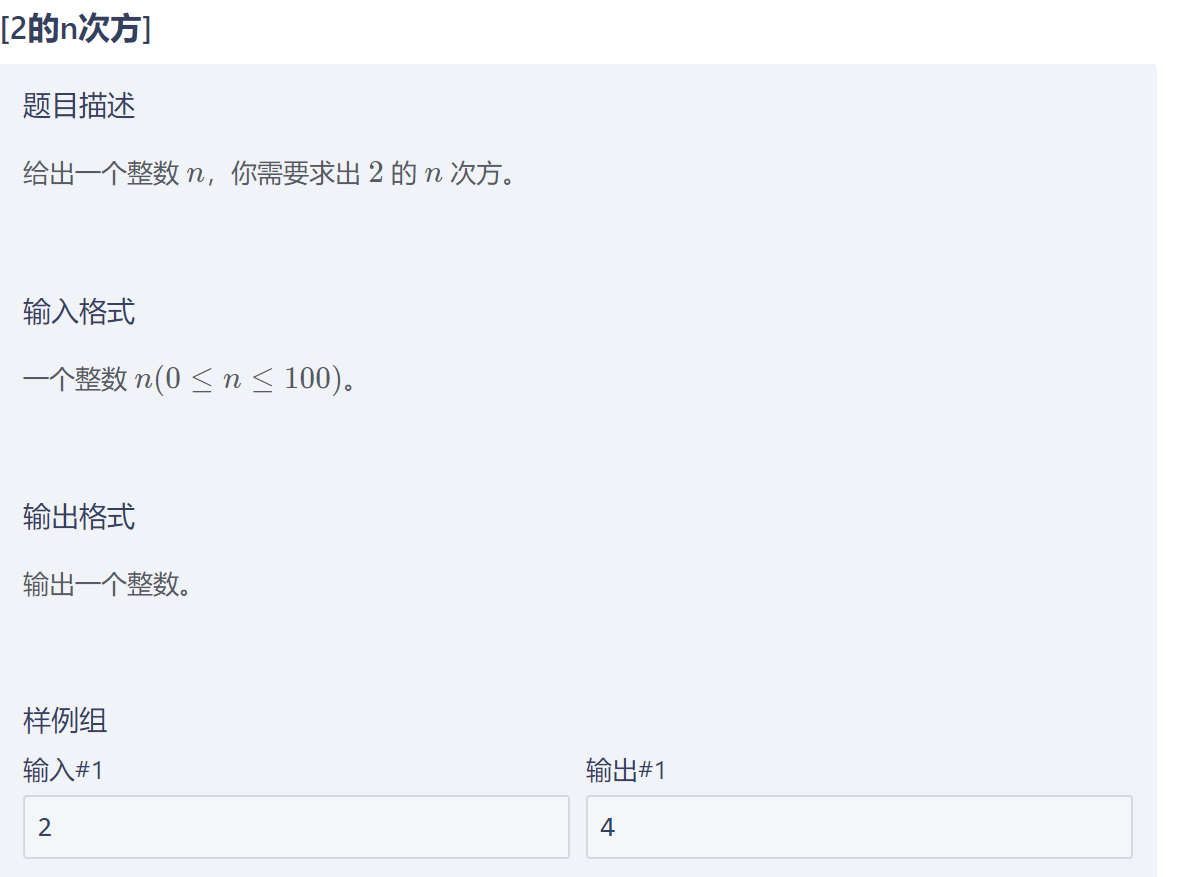
[2的n次方]
高精度乘法复习资料:https://www.cnblogs.com/jayxuan/p/18287673

重复做以下操作 $n $ 次:对每一位乘以 $2 $,然后进位。(当然也可以使用正常的高精度乘法)【参考代码】 #include<bits/stdc++.h> using namespace std;int ans[59]; int main() {int n;cin >> n;ans[0] = 1;for (int i = 0; i < n; i++) {for (int j = 0; j < 50; j++) {ans[j] *= 2;}for (int j = 0; j < 50; j++) {ans[j + 1] += ans[j] / 10;ans[j] %= 10;}}int len = 49;while (!ans[len]) len--;for (int i = len; i >= 0; i--) cout << ans[i];return 0; }
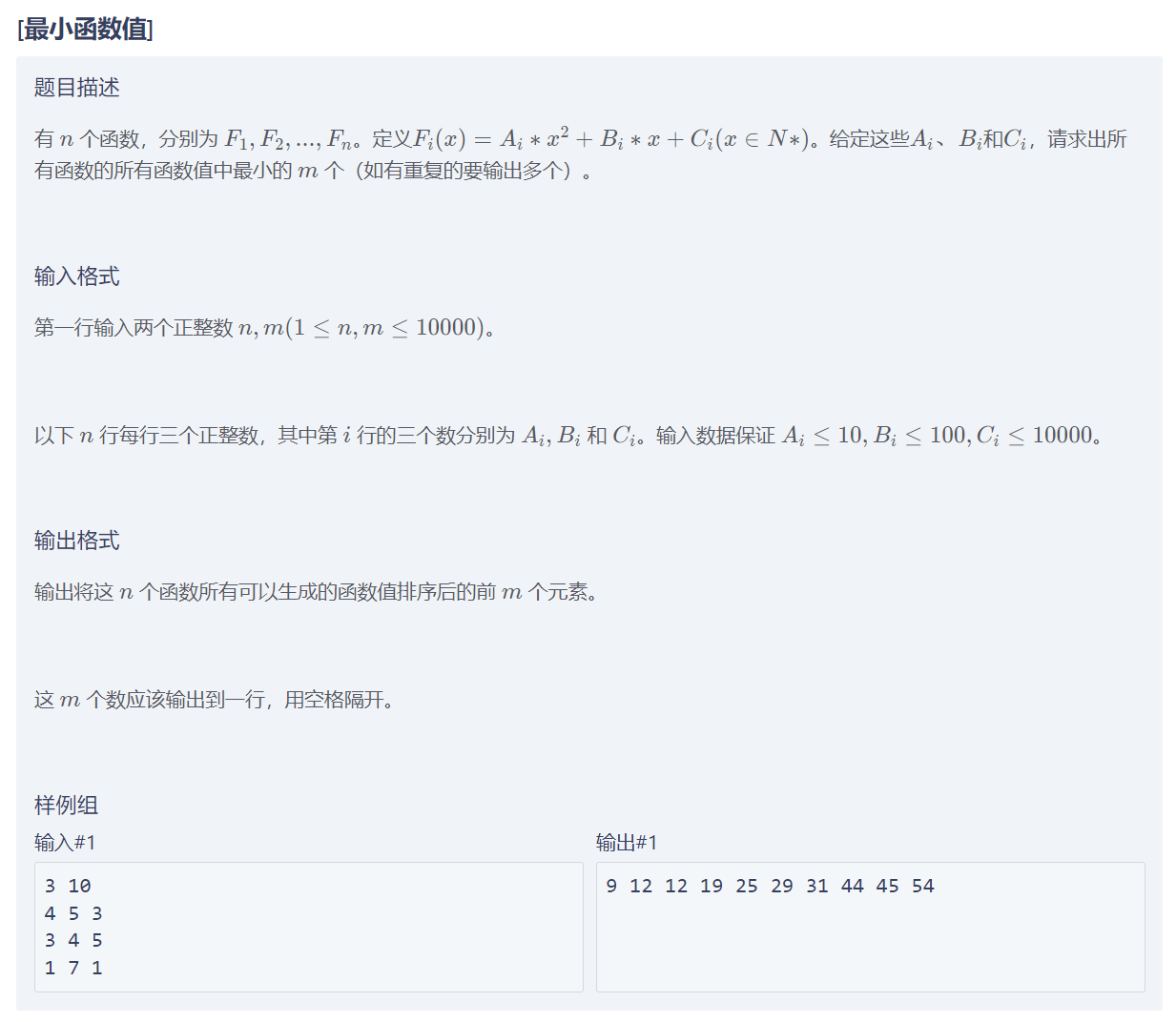
[最小函数值]
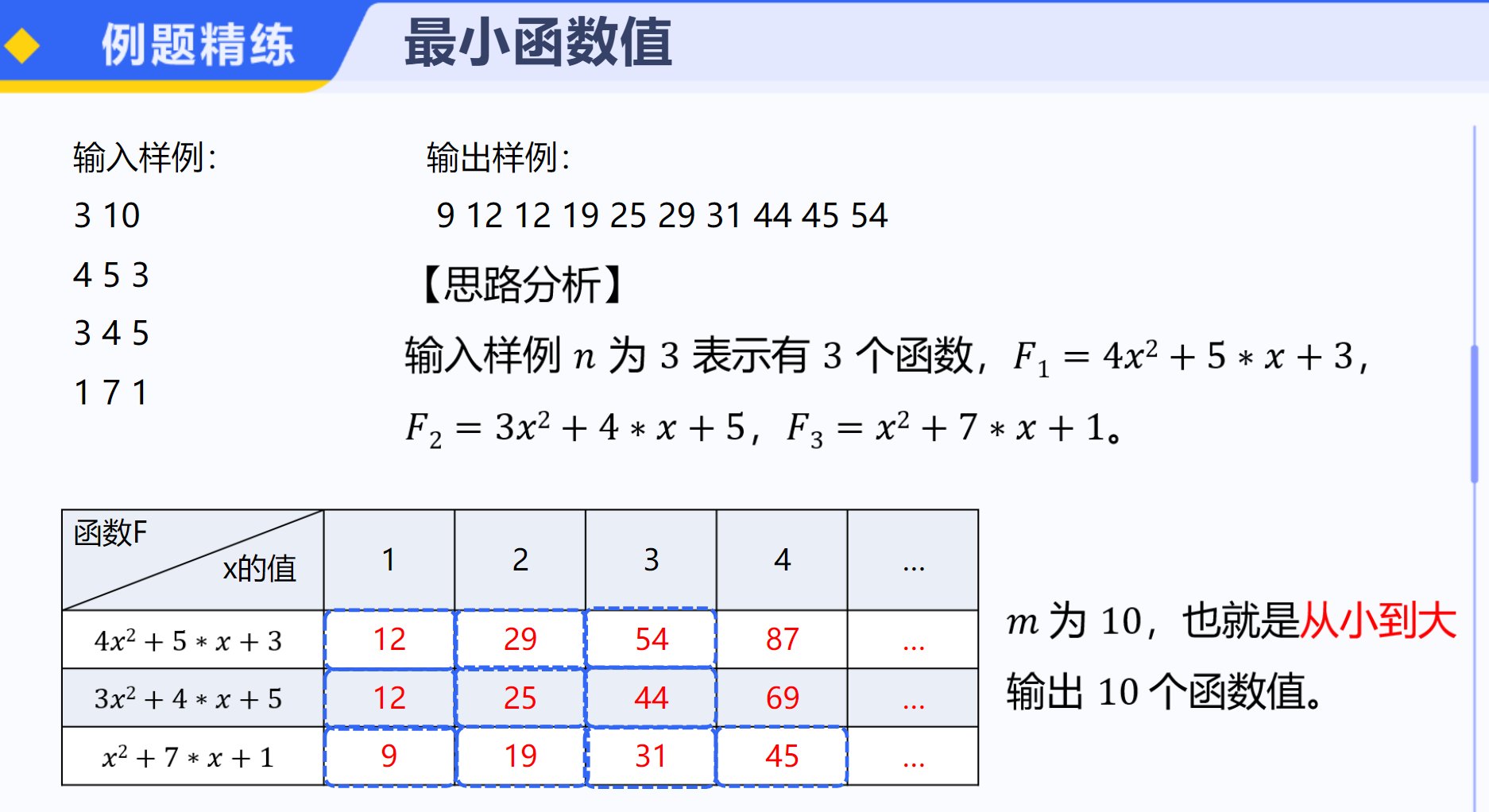

#include<bits/stdc++.h> using namespace std; int main() { int n, m; // n 表示函数个数,m 表示每个函数考虑的 x 的范围(1 到 m) cin >> n >> m; priority_queue<int> q; // 使用最大堆(默认)来存储当前遇到的最小值 for (int i = 0; i < n; i++) { // 遍历每个函数 int a, b, c; // 函数 ax^2 + bx + c 的系数 cin >> a >> b >> c; for (int j = 1; j <= m; j++) { // 遍历 x 的取值范围(1 到 m) int tem = a * j * j + b * j + c; // 计算当前 x 值下的函数结果 if (q.size() < m) q.push(tem); // 如果堆中元素少于 m 个,直接加入 else if (q.top() > tem) { // 如果堆顶元素(即当前最大元素)大于当前计算值 q.pop(); // 弹出堆顶元素 q.push(tem); // 加入当前计算值 } else break; // 如果当前计算值不小于堆顶元素,则无需继续计算,因为后续值会更大 } } vector<int> ve; // 用于存储所有函数的前 m 小值 while (q.size()) { // 当堆不为空时 ve.push_back(q.top()); // 将堆顶元素(当前最大值,即所有值中的最小之一)加入向量 q.pop(); // 弹出堆顶元素 } // 由于我们需要从大到小输出,而 vector 默认从小到大存储,所以逆序遍历 for (int i = ve.size() - 1; i >= 0; i--) cout << ve[i] << " "; return 0; }
[奖金]

拓扑排序复习:https://www.cnblogs.com/jayxuan/p/18238671

这段代码实现了一个基于图论的问题,通常被称为“奖金分配”或“拓扑排序中的最长路径”问题。在这个问题中,你有一个有向无环图(DAG),图中的每个节点代表一个员工,每条有向边从员工A指向员工B表示A是B的直接上级。公司决定根据员工的层级(即从CEO到每个员工的最长路径长度)来分配奖金,CEO的层级为1,并且每个员工的奖金是其层级的100倍。如果图中存在环,则无法确定层级,输出"Poor Xed"。#include<bits/stdc++.h> using namespace std; const int maxn = 1e4 + 9; // 定义最大节点数 vector<int> ve[maxn]; // 邻接表,存储每个节点的直接下级列表 int deg[maxn]; // 存储每个节点的入度(即有多少节点指向它) int ans[maxn]; // 存储每个节点的层级(奖金的倍数) int main() { int n, m; // n是节点数(员工数),m是边数(关系数) cin >> n >> m; // 读取边信息,构建邻接表和入度数组 for (int i = 0; i < m; i++) { int a, b; cin >> a >> b; ve[b].push_back(a); // b是a的上级,所以a是b的下级 deg[a]++; // a的入度加1 } queue<int> q; // 使用队列进行拓扑排序 // 将所有入度为0的节点(即没有上级的节点,可能是CEO)加入队列,并初始化其层级为1(奖金为100) for (int i = 1; i <= n; i++) { if (deg[i] == 0) q.push(i), ans[i] = 100; } // 拓扑排序过程 while (q.size()) { int r = q.front(); // 取出队列中的节点 q.pop(); // 遍历该节点的所有下级 for (int i = 0; i < ve[r].size(); i++) { int y = ve[r][i]; // 更新下级的层级为当前节点层级加1(奖金倍数增加) ans[y] = max(ans[y], ans[r] + 1); // 下级的入度减1 if (--deg[y] == 0) q.push(y); // 如果下级入度变为0,则加入队列继续处理 } } // 检查是否所有节点都被处理(即图中是否存在环) for (int i = 1; i <= n; i++) { if (deg[i]) { // 如果有节点的入度不为0,说明存在环 cout << "Poor Xed"; // 输出"Poor Xed"并结束程序 return 0; } } int sum = 0; // 计算所有员工的总奖金 for (int i = 1; i <= n; i++) sum += ans[i]; // 这里实际上计算的是奖金的倍数之和,如果需要真实奖金,应乘以100 // 注意:如果题目要求输出的是奖金总额(即倍数乘以100),则应将sum乘以100后输出 cout << sum; // 输出奖金的倍数之和(如果需要,可以乘以100后输出) return 0; }
[最短网络]
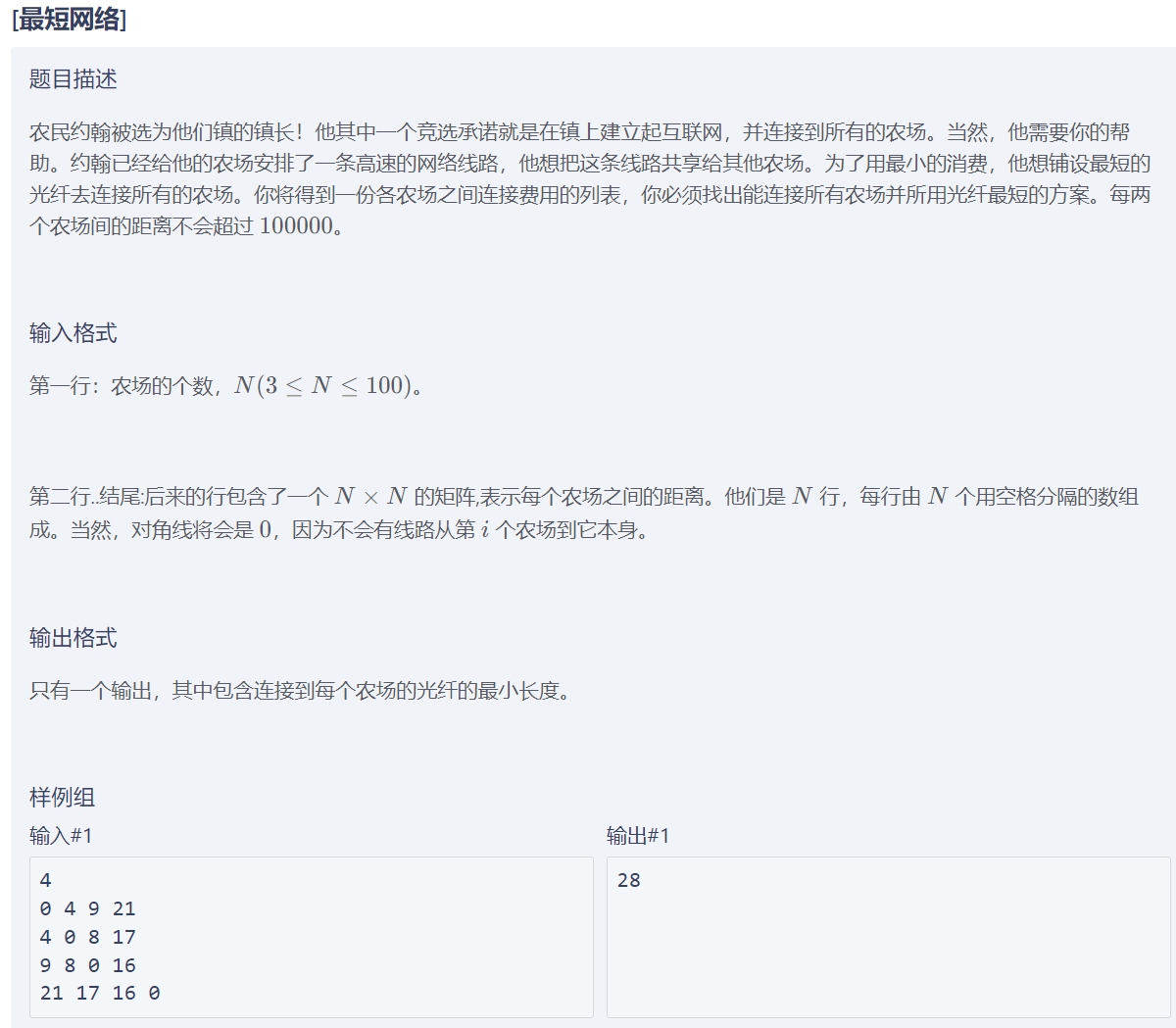
最小生成树复习:https://www.cnblogs.com/jayxuan/p/18263315
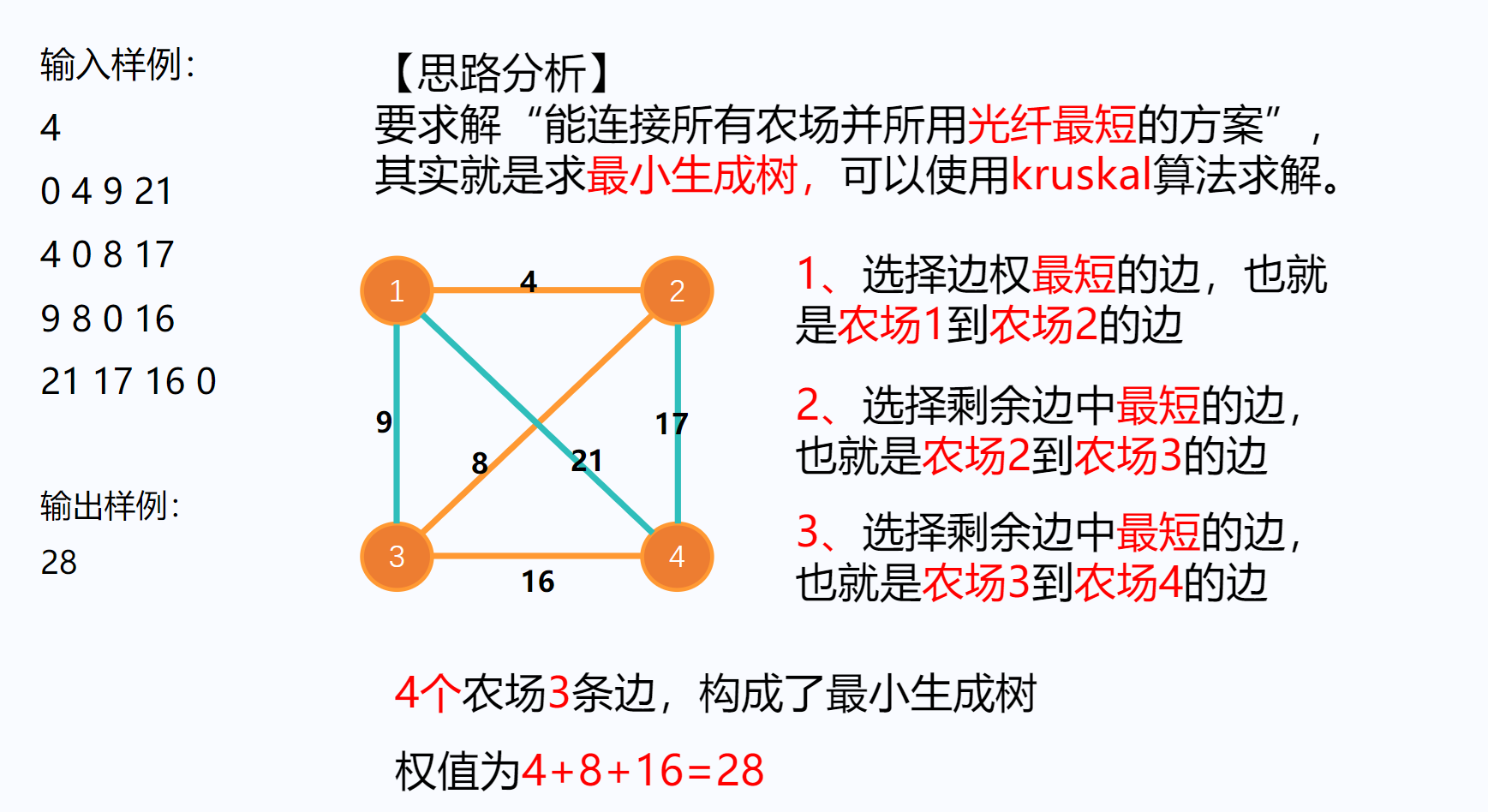

【算法分析】 题目是要求“能连接所有农场并所用光纤最短的方案”,这其实就是最小生成树。将所有边提取出来,存到数组里(重复的边可以不存储),然后跑最小生成树即可。【参考代码】 #include<bits/stdc++.h> using namespace std; struct node {int x, y, w; }; vector<node> ve; bool cmp(node A, node B) {return A.w < B.w; } int fa[109]; int get(int x) {if (fa[x] == x) return x;return fa[x] = get(fa[x]); } void merge(int x, int y) {fa[get(x)] = get(y); } int main() {int n;cin >> n;for (int i = 1; i <= n; i++) fa[i] = i;for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {int a;cin >> a;if (j > i) ve.push_back({ i,j,a });}}sort(ve.begin(), ve.end(), cmp);int ans = 0;for (int i = 0; i < ve.size(); i++) {if (get(ve[i].x) == get(ve[i].y)) continue;ans += ve[i].w;merge(ve[i].x, ve[i].y);}cout << ans;return 0; }
12课-阶段测评练习课
选择题1
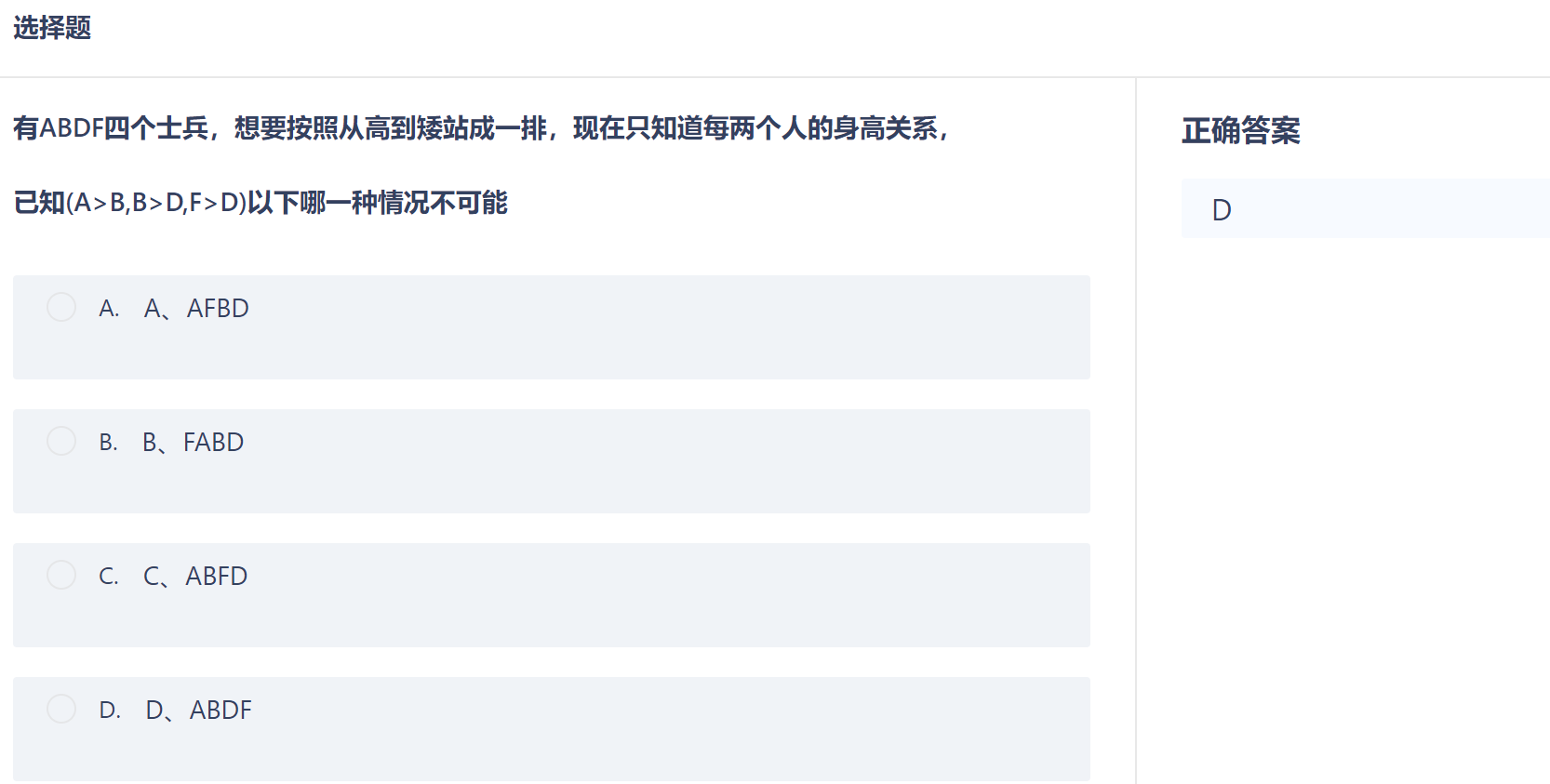
选择题2:构建大根堆复习
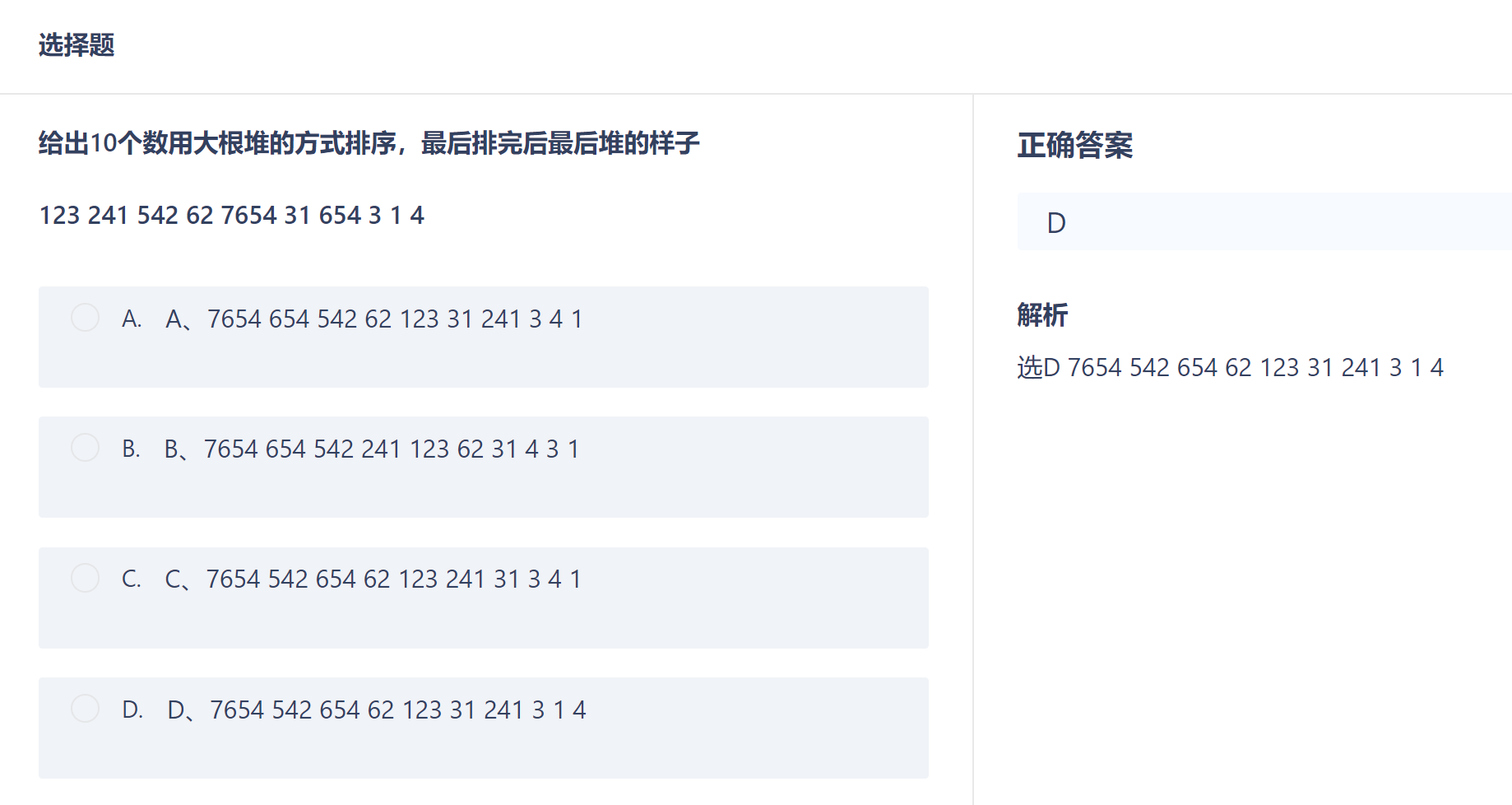
选择题3:并查集知识复习

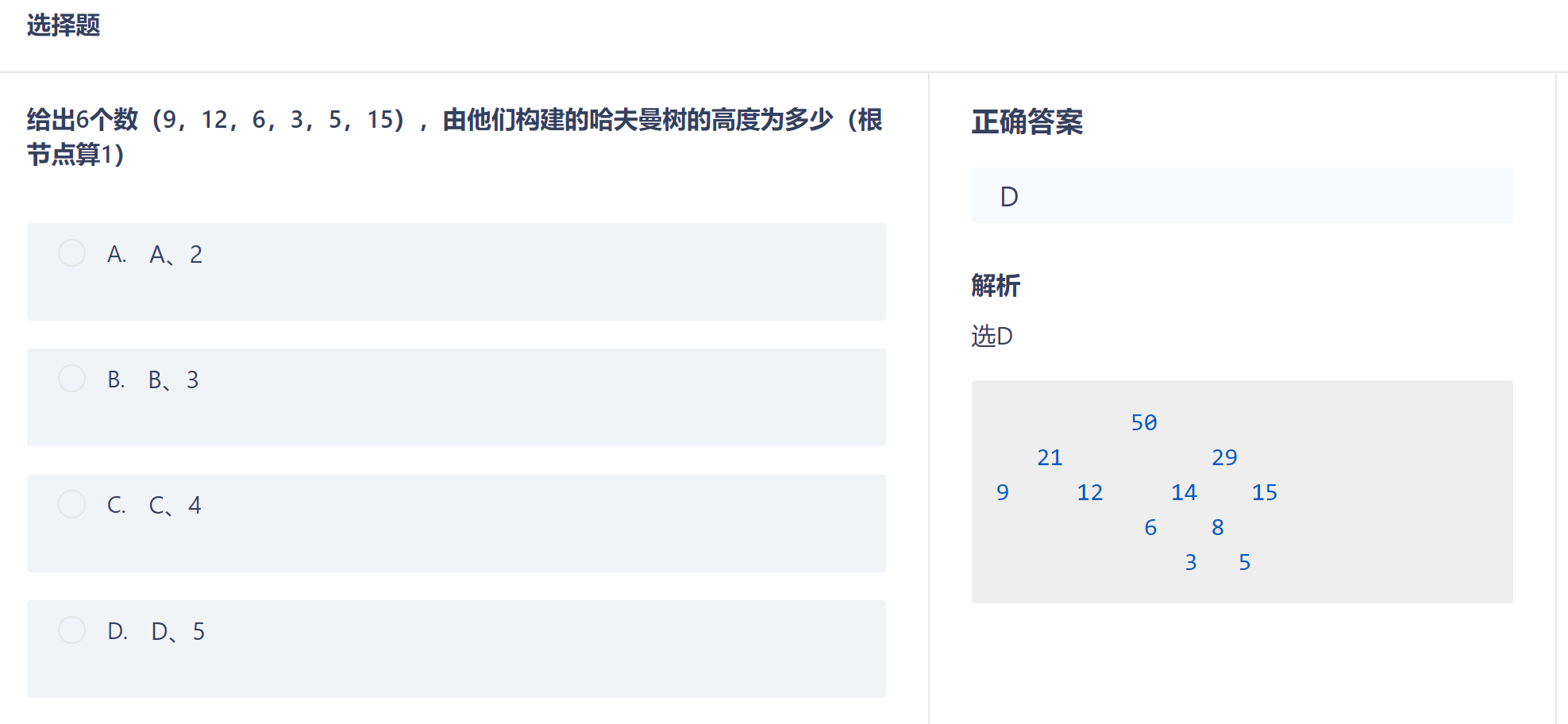
选择题4:哈夫曼树 :https://www.cnblogs.com/jayxuan/p/18176107
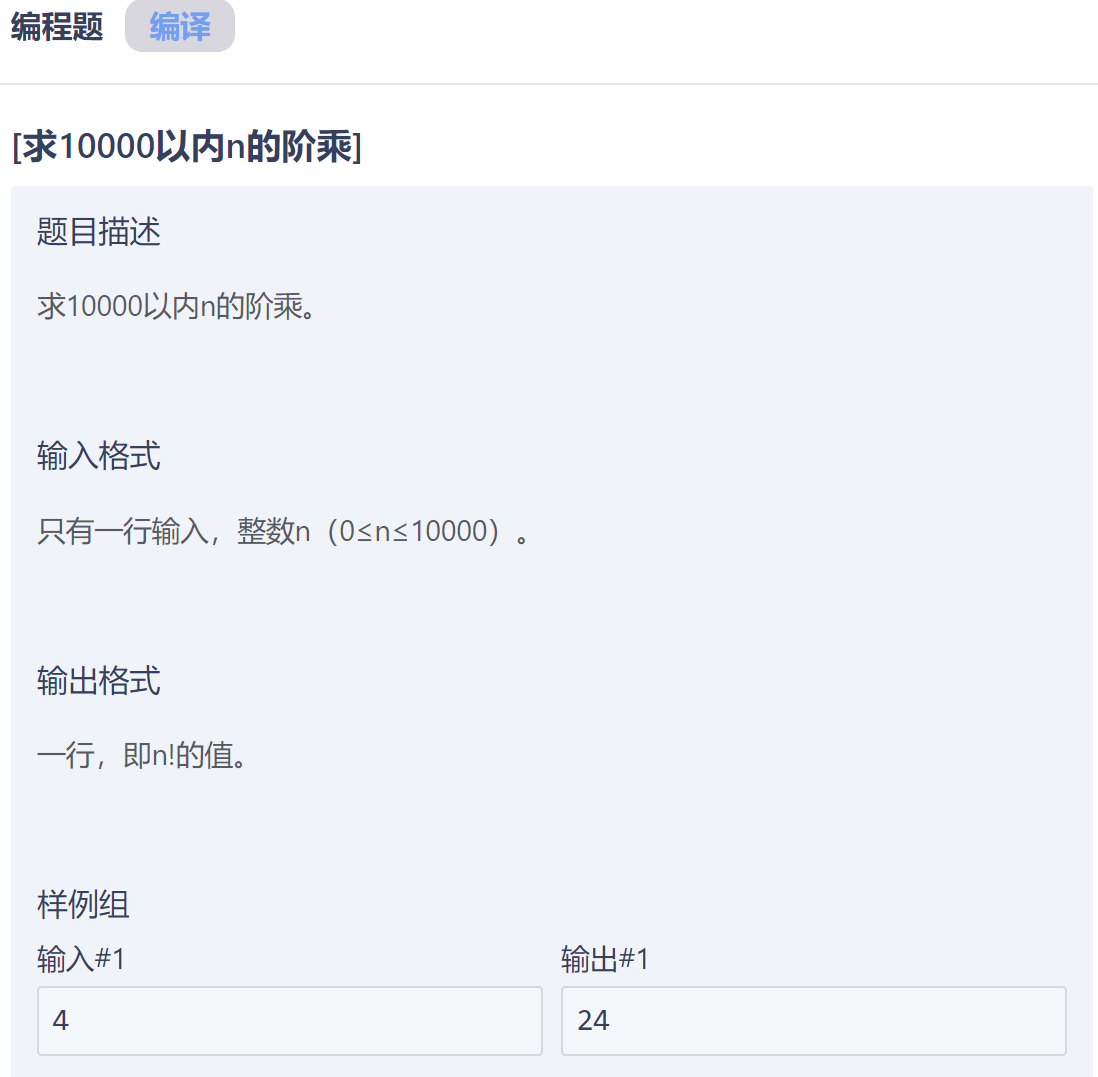
组合题目

最小生成树复习链接:https://www.cnblogs.com/jayxuan/p/18263315
这是一份C++ prim的代码,小码君不小心打翻了墨水,有几处需要你来补齐
#include<bits/stdc++.h>
using namespace std;
int n,m;
struct node{int to,tot;
};
int dis[200005];
bool vis[200005];
vector<node>g[200005];
int sum=0;
void prim(){memset(vis,false,sizeof vis);memset(dis,666666,sizeof dis);【________1________】for(int i=1;i<=n;i++){int x,zx=INT_MAX-1;for(int j=1;j<=n;j++){if(【________2________】&&dis[j]<zx){zx=dis[j];x=j;}}【________3________】for(int j=0;【________4________】;j++){int v=g[x][j].to;int tot=g[x][j].tot;if(!vis[v]&&dis[v]>tot){dis[v]=tot;}} 【________5________】}return ;
}
int main(){cin>>n>>m;for(int i=1;i<=m;i++){int x,y,z;cin>>x>>y>>z;g[x].push_back({y,z});g[y].push_back({x,z});}prim();cout<<sum<<endl;return 0;
}
(一)
-
A.
A、dis[1]=0;
-
B.
B、dis[1]=1;
-
C.
C、vis[1]=0;
-
D.
D、vis[1]=1;
(二)
-
A.
A、!vis[i]
-
B.
B、!vis[j]
-
C.
C、vis[i]
-
D.
D、vis[j]
(三)
-
A.
A、dis[x]=1;
-
B.
B、dis[x]=0;
-
C.
C、vis[x]=false;
-
D.
D、vis[x]=true;
(四)
-
A.
A、j<g[x].size()
-
B.
B、j<n
-
C.
C、j<m
-
D.
D、j<=n
(五)
-
A.
A、sum=max(dis[x],sum);
-
B.
B、sum=min(dis[x],sum);
-
C.
C、sum+=dis[x];
-
D.
D、sum+=vis[x];
-

【算法分析】 高精度模拟即可【参考代码】 #include<bits/stdc++.h> using namespace std; int a[40000],h; //记录最高位,节省时间 void f(int n){ //函数递归if(n==1){a[0]=1;return;}f(n-1);int x=0;for(int i=0;i<=h+4;i++){ //利用x记录进位,一次循环搞定a[i]*=n; //n小,直接乘a[i]+=x;x=a[i]/10;a[i]%=10;}h+=4;while(!a[h])h--; } int main(){int n;cin>>n;f(n);for(int i=h;i>=0;i--)cout<<a[i];return 0; }
[无线通讯网] 题目描述 国防部计划用无线网络连接若干个边防哨所。2 种不同的通讯技术用来搭建无线网络;每个边防哨所都要配备无线电收发器;有一些哨所还可以增配卫星电话。任意两个配备了一条卫星电话线路的哨所(两边都ᤕ有卫星电话)均可以通话,无论他们相距多远。而只通过无线电收发器通话的哨所之间的距离不能超过 D,这是受收发器的功率限制。收发器的功率越高,通话距离 D 会更远,但同时价格也会更贵。收发器需要统一购买和安装,所以全部哨所只能选择安装一种型号的收发器。换句话说,每一对哨所之间的通话距离都是同一个 D。你的任务是确定收发器必须的最小通话距离 D,使得每一对哨所之间至少有一条通话路径(直接的或者间接的)。提示 对于 100% 的数据保证:1≤S≤100,S<P≤500,0≤x,y≤10000。输入格式 输入数据第 1 行,2 个整数 S 和 P,S 表示可安装的卫星电话的哨所数,P 表示边防哨所的数量。接下里 P 行,每行两个整数 x,y 描述一个哨所的平面坐标 (x,y),以 km 为单位。输出格式 第 1 行,1 个实数 D,表示无线电收发器的最小传输距离,精确到小数点后两位。样例组 输入#1输出#12 4 0 100 0 300 0 600 150 750 212.13

#include<bits/stdc++.h> using namespace std; // 节点数n和边数m int n,m; // 并查集数组,用于快速查找和合并集合 int arr[100005]; // 边的结构体,包含两个端点和边的权重(距离) struct node{ double x; // 边的起点 double y; // 边的终点 double z; // 边的权重(两点间的距离) }; // 存储所有边的数组 node a[2005]; // 路径(但这里命名不准确,应为边) node lss[500005]; // 存储所有计算得到的边和它们的权重(距离),lss可能代表line segment或者length sorted segments // 比较函数,用于对边按权重进行排序 bool cmp(node x,node y){ return x.z<y.z; } // 查找函数,用于并查集,返回元素所在集合的根 int find(int x){ if(x==arr[x])return x; return arr[x]=find(arr[x]); // 路径压缩优化 } // 合并函数,将两个元素所在的集合合并 void hb(int x,int y){ int xx=find(x); int yy=find(y); if(xx!=yy) arr[xx]=yy; // 只在两个元素不在同一集合时合并 } int main(){ cin>>n>>m; // 输入节点数和边数 for(int i=1;i<=m;i++){ arr[i]=i; // 初始化并查集,每个元素自己是一个集合 } for(int i=1;i<=m;i++){ cin>>a[i].x>>a[i].y; // 输入每条边的两个端点 a[i].z = 0; // 这里a[i].z没有直接赋值,但在实际使用中应该通过计算得到,但在这个代码片段中它没有被使用 } int t=0; // 用于记录lss数组中边的数量 for(int i=1;i<=m;i++){ for(int j=1;j<i;j++){ t++; lss[t].x=i; lss[t].y=j; lss[t].z=sqrt((a[i].x-a[j].x)*(a[i].x-a[j].x)+(a[i].y-a[j].y)*(a[i].y-a[j].y)); // 计算两点间的欧几里得距离 } } int w=0; // 记录已加入MST的边数 sort(lss+1,lss+1+t,cmp); // 按边的权重对lss数组进行排序 for(int i=1;i<=t;i++){ if(find(lss[i].x)!=find(lss[i].y)){ // 如果当前边的两个端点不在同一集合中 hb(lss[i].x,lss[i].y); // 合并这两个集合 w++; // 增加已加入MST的边数 if(w==m-n+1){ // 当加入的边数等于节点数减一时,MST构建完成 printf("%.2f",lss[i].z); // 输出最后一条加入MST的边的权重(即MST的总权重) return 0; } } } // 如果无法构建MST(例如,图中存在多个连通分量且节点数小于n),则这里会返回,但题目没有给出明确的处理 return 0; }
[小码君的账单] 题目描述 小码君在一次聚会中,不慎遗失了自己的钱包,在接下来的日子,面对小码君的将是一系列的补卡手续和堆积的账单… 在小码君的百般恳求下,老板最终同意延缓账单的支付时间。可老板又提出,必须从目前还没有支付的所有账单中选出面额最大和最小的两张,并把他们付清。还没有支付的账单会被保留到下一天。 请你帮他计算出支付的顺序。输入格式 第1行:一个正整数N(N≤100),表示小码君补办银联卡总共的天数。第2行到第N+1 行:每一行描述一天中收到的帐单。先是一个非负整数M≤100,表示当天收到的账单数,后跟M个正整数(都小于1000000),表示每张帐单的面额。输入数据保证每天都可以支付两张帐单。输出格式 输出共N 行,每行两个用空格分隔的整数,分别表示当天支付的面额最小和最大的支票的面额。样例组 输入#1输出#14 3 3 6 5 2 8 2 3 7 1 7 0 3 6 2 8 1 7 5 7

【算法分析】 设大顶堆与小顶堆,里面保存的数据类型为账单类型。大顶堆中账单面额更大的更优先,小顶堆中账单面额更小的更优先。然后每天从大小根堆的顶部取出一个【参考代码】 #include<bits/stdc++.h> using namespace std;int n,m,cnt,a[1500010],v[1500010]; pair<int,int>v1,v2;priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >q1; priority_queue<pair<int,int> >q2;int main(){scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&m);for(int j=cnt+1;j<=cnt+m;j++){scanf("%d",&a[j]);q1.push(make_pair(a[j],j));q2.push(make_pair(a[j],j));}while(v[q1.top().second])q1.pop();v1=q1.top();printf("%d ",v1.first);v[v1.second]=1;while(v[q2.top().second])q2.pop();v2=q2.top();printf("%d\n",v2.first);v[v2.second]=1;cnt+=m;} }