题目:
一个桶里一共有a个白球和b个黑球。每次拿出2个球,并且每个球被拿出的概率相等。
如果拿出一黑一白,就往桶里放进一个黑球;如果拿出两个黑或者两个白,就往桶里放进一个白球。
求:最后只剩一个黑球的概率是多少?
答案:
如果黑球个数是偶数,最后剩下为黑球的概率是0%;
如果黑球个数是奇数,最后剩下为黑球的概率是100%。
解析:
由题可知:黑+白=黑 、 白+黑=黑 、 白+白=白 、 黑+黑=白
假设白球为0,黑球为1 :1 + 0 =1 、0 + 1 =1 、0 + 0 =0 、1 + 1 =0 。
可知这是一个异或问题。 1 ^ 0 =1 、0 ^ 1 =1 、0 ^ 0 =0 、1 ^ 1 =0 。 每拿出两个球就做一次异或运算,然后把结果放进桶里。
就等于把桶里所有的球都进行一次异或运算。
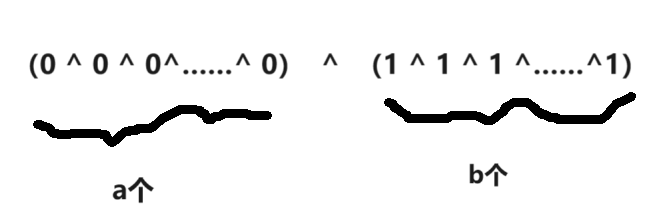
因为不管是奇数个0还是偶数个0,最后结果都是0,所以剩黑球的概率和白球没有关系。
当黑球的个数是偶数时,所有黑球的异或结果是0, 最后 0^0 = 0, 最后剩白球,所以剩黑球的概率是0%;
当黑球的个数是奇数时,所有黑球的异或结果是1, 最后 0^1 = 1,最后剩黑球,所以剩黑球的概率是100%。