T1
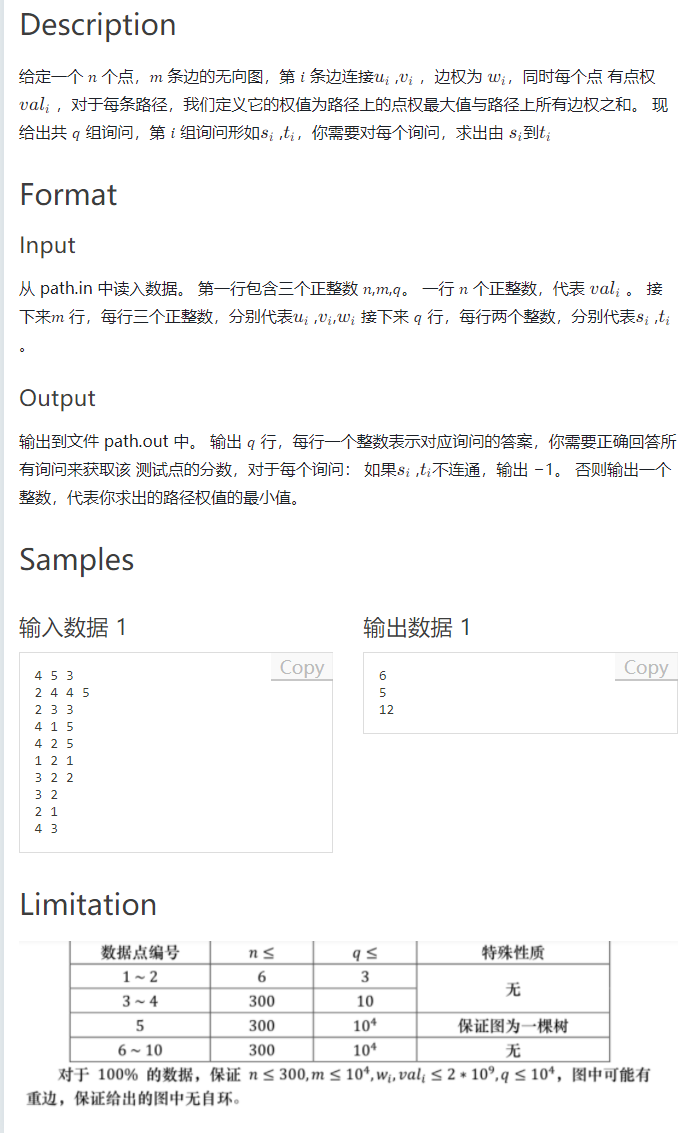
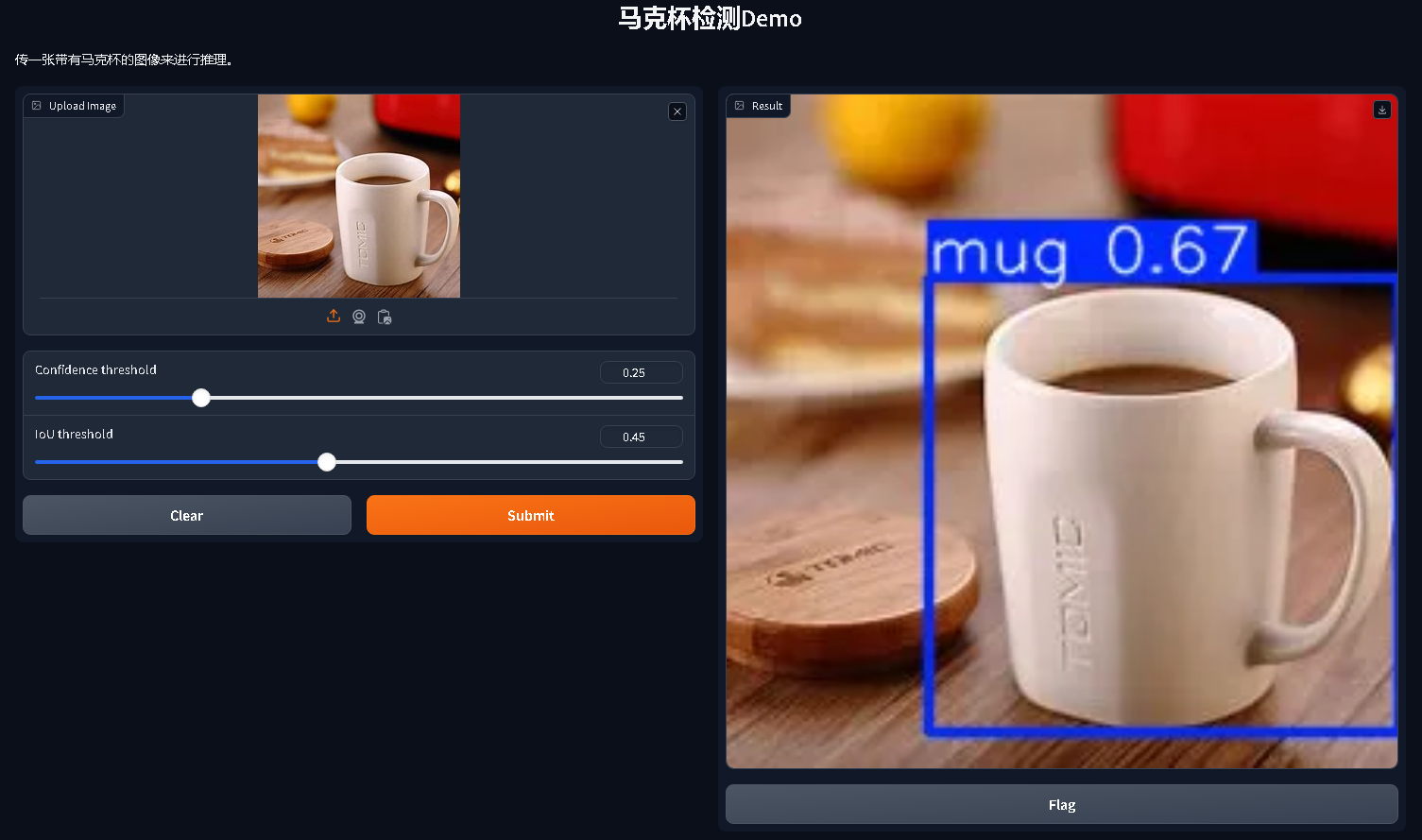
很明显的最短路floyed算法,但是这个最大的点权却不是很好维护,但我们可以想到枚举最大的点权其实就可以相当于枚举floyed中的k,那么这时我们要对k进行一个排序操作,使得我们每次枚举的中转点k为枚举经过路径的点权最大的点从而达到同时走最短路并维护点权最大值。
点击查看代码
#include<bits/stdc++.h>
using namespace std;#define int long long
const int N=400;
int n,m,q;struct lmy
{int id,w;
}pos[N];
int rk[N];
int dis[N][N],ans[N][N];bool comp(lmy a,lmy b)
{return a.w<b.w;
}
signed main()
{
// freopen("path.in","r",stdin);
// freopen("path.out","w",stdout); scanf("%lld%lld%lld",&n,&m,&q);for(int i=1;i<=n;i++){scanf("%lld",&pos[i].w);pos[i].id=i;}sort(pos+1,pos+1+n,comp);for(int i=1;i<=n;i++){rk[pos[i].id]=i;}memset(dis,0x3f,sizeof dis);for(int i=1;i<=n;i++){dis[i][i]=0;}for(int i=1;i<=m;i++){int x,y,dt;scanf("%lld%lld%lld",&x,&y,&dt);dis[rk[x]][rk[y]]=min(dis[rk[x]][rk[y]],dt);dis[rk[y]][rk[x]]=min(dis[rk[y]][rk[x]],dt);}memset(ans,0x3f,sizeof ans);for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i==j) continue;dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);if(dis[i][j]==dis[i][k]+dis[k][j]) ans[i][j]=min(ans[i][j],dis[i][j]+max({pos[i].w,pos[j].w,pos[k].w}));}}}for(int i=1;i<=q;i++){int s,t;scanf("%lld%lld",&s,&t);if(ans[rk[s]][rk[t]]>=0x3f3f3f3f3f3f3f3f) printf("-1\n");else printf("%lld\n",ans[rk[s]][rk[t]]);}
}

首先就是可以想到维护一个二维前缀和。
然后像这种具有单调性的数列(只维护正整数的前缀和)维护我们可以想到用单调队列。
那我们就可以一行一行的删去看是否符合条件,
最后剩下的我们就一点一点凑。
点击查看代码
#include<bits/stdc++.h>
using namespace std;#define int long long
const int N=2010;
int n,k;
int s[N][N],g[N][N];
int up[N][N];
int sta[N],tp;
int l[N],r[N];
int ax,ay,bx,by;
int get(int a,int b,int c,int d)
{return s[c][d]+s[a-1][b-1]-s[a-1][d]-s[c][b-1];
}
signed main()
{
// freopen("matrix.in","r",stdin);
// freopen("matrix.out","w",stdout);scanf("%lld%lld",&k,&n);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){scanf("%lld",&g[i][j]);if(g[i][j]>=k&&g[i][j]<=2*k){printf("%lld %lld %lld %lld",j,i,j,i);exit(0);}s[i][j]=s[i][j-1]+g[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){s[i][j]=s[i-1][j]+s[i][j];if(s[i][j]>=k&&s[i][j]<=2*k){printf("1 1 %lld %lld",j,i);exit(0);}}}int mx=0;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(g[i][j]<k){up[i][j]=up[i-1][j]+1;}}sta[tp=1]=0;up[i][0]=-1;for(int j=1;j<=n;j++){while(tp&&up[i][sta[tp]]>=up[i][j]) tp--;l[j]=sta[tp]+1;sta[++tp]=j;}sta[tp=1]=n+1;up[i][n+1]=-1;for(int j=n;j>=1;j--){while(tp&&up[i][sta[tp]]>=up[i][j]) tp--;r[j]=sta[tp]-1;sta[++tp]=j;if(up[i][j]){int now=get(i-up[i][j]+1,l[j],i,r[j]);if(now>=k&&now<=2*k){printf("%lld %lld %lld %lld",l[j],i-up[i][j]+1,r[j],i);exit(0);}if(now>mx){mx=now;ax=i-up[i][j]+1;ay=l[i];bx=i;by=r[j];}}}}if(mx<k) {printf("NTE");exit(0);}for(int i=bx;i>=ax;i--){int now=get(i,ay,i,by);if(now>=k&&now<=2*k){printf("%lld %lld %lld %lld",ay,i,by,i);exit(0);} if(now>2*k){mx=now;for(int j=by;j>=ay;j--){mx-=g[i][j];if(mx>=k&&mx<=k*2){printf("%lld %lld %lld %lld",ay,i,j-1,i);exit(0);}}}else{mx-=now;if(mx>=k&&mx<=2*k){printf("%lld %lld %lld %lld",ay,ax,by,i-1);exit(0);}}}
}
T3

区间修改和查询很容易的想到了线段树,但赛时没打出来。
先来看下欧拉函数的定义:
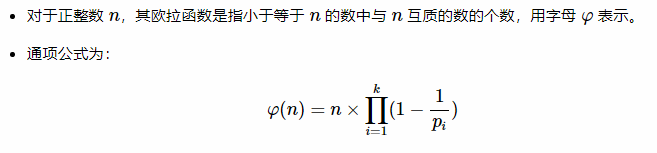
那注意一下300这个数字,1到300之间有62个质数,刚好在long long范围内,我们可以考虑用状态压缩来维护这个有关质数的问题,同时我们把欧拉函数分成两部分分开来处理,先预处理出来这62个质数的(p-1)/p,那我们线段树就只需要维护区间每个数的质数情况和乘积。
点击查看代码
#include<bits/stdc++.h>
using namespace std;#define int long long
const int mod=1e9+7;
const int N=1e6;
int cnt=62,pr[70]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,211,223,227,229,233,239,241,251,257,263,269,271,277,281,283,293};
int n,m;
int a[N],inv[N],tp[N];int qpow(int a,int b)
{int ans=1;while(b){if(b&1){ans=ans*a%mod;}a=a*a%mod;b=b>>1;}return ans;
}
#define lson (rt<<1)
#define rson (rt<<1|1)struct lmy
{int l,r;int pd,lz,fc,lf;lmy(){pd=lz=1;fc=lf=0; }
}tr[N<<2];void pushup(int rt)
{tr[rt].pd=tr[lson].pd*tr[rson].pd%mod;tr[rt].fc=tr[lson].fc|tr[rson].fc;
}
void pushdown(int rt)
{tr[lson].pd=tr[lson].pd*qpow(tr[rt].lz,tr[lson].r-tr[lson].l+1)%mod;tr[rson].pd=tr[rson].pd*qpow(tr[rt].lz,tr[rson].r-tr[rson].l+1)%mod;tr[lson].lz=tr[lson].lz*tr[rt].lz%mod;tr[rson].lz=tr[rson].lz*tr[rt].lz%mod;tr[rt].lz=1;tr[lson].fc|=tr[rt].lf;tr[rson].fc|=tr[rt].lf;tr[lson].lf|=tr[rt].lf;tr[rson].lf|=tr[rt].lf;tr[rt].lf=0;
}
void build(int rt,int l,int r)
{tr[rt].l=l;tr[rt].r=r;if(l==r){tr[rt].pd=a[l];for(int i=0;i<cnt;i++){if(a[l]%pr[i]==0) tr[rt].fc|=((1ll)<<i);}tr[rt].lz=1;return ;}int mid=(l+r)>>1;build(lson,l,mid);build(rson,mid+1,r);pushup(rt);
}
void update(int rt,int l,int r,int c,int f)
{if(l<=tr[rt].l&&r>=tr[rt].r){tr[rt].pd=tr[rt].pd*qpow(c,tr[rt].r-tr[rt].l+1)%mod;tr[rt].lz=tr[rt].lz*c%mod;tr[rt].fc|=f;tr[rt].lf|=f;return ;}pushdown(rt);int mid=(tr[rt].l+tr[rt].r)>>1;if(l<=mid) update(lson,l,r,c,f);if(r>mid) update(rson,l,r,c,f);pushup(rt);
}
int query_pd(int rt,int l,int r)
{if(l<=tr[rt].l&&tr[rt].r<=r){return tr[rt].pd;}int ans=1;pushdown(rt);int mid=(tr[rt].l+tr[rt].r)>>1;if(l<=mid) ans=ans*query_pd(lson,l,r)%mod;if(r>mid) ans=ans*query_pd(rson,l,r)%mod;return ans;
}
int query_fc(int rt,int l,int r)
{if(l<=tr[rt].l&&tr[rt].r<=r){return tr[rt].fc;}int ans=0;pushdown(rt);int mid=(tr[rt].l+tr[rt].r)>>1;if(l<=mid) ans|=query_fc(lson,l,r);if(r>mid) ans|=query_fc(rson,l,r);return ans;
}
void init()
{for(int i=2;i<=300;i++){inv[i]=qpow(i,mod-2);}for(int i=0;i<=cnt-1;i++){tp[i]=inv[pr[i]]*(pr[i]-1)%mod;}
}
signed main()
{freopen("array.in","r",stdin);freopen("array.out","w",stdout);init();scanf("%lld%lld",&n,&m);for(int i=1;i<=n;i++) scanf("%lld",&a[i]);build(1,1,n);for(int i=1;i<=m;i++){char op[20];scanf("%s",op);int l,r;scanf("%lld%lld",&l,&r);if(op[0]=='1'){int z;scanf("%lld",&z);int f=0;for(int j=0;j<cnt;j++){if(z%pr[j]==0) f|=((1ll)<<j);}update(1,l,r,z,f);}else{int x=query_pd(1,l,r);int y=query_fc(1,l,r);int ans=x;
// cout<<ans<<" ";for(int j=0;j<cnt;j++){if((y>>j)&1) ans=ans*tp[j]%mod;}printf("%lld\n",ans);}}
}