Codeforces 956 Div2

期末考试结束，开始训练

A. Array Divisibility

----------------------------------题解----------------------------

简单的构造题，要让数组a里面的下表为1<=k<=n的数以及下表为(k的因数)的数加起来的和能被K整除，那我们只需要让每一个k的因数都能被k整除就行了，直接让每一个编号i处所带的元素为i*i便可以实现，不信你就随便找几个k试一下例如(2,3,5)

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int main()
{int t;cin>>t;while(t--){int n;cin>>n;for(int i=1;i<=n;i++){cout<<i*i<<" ";}cout<<endl;}
}

B. Corner Twist

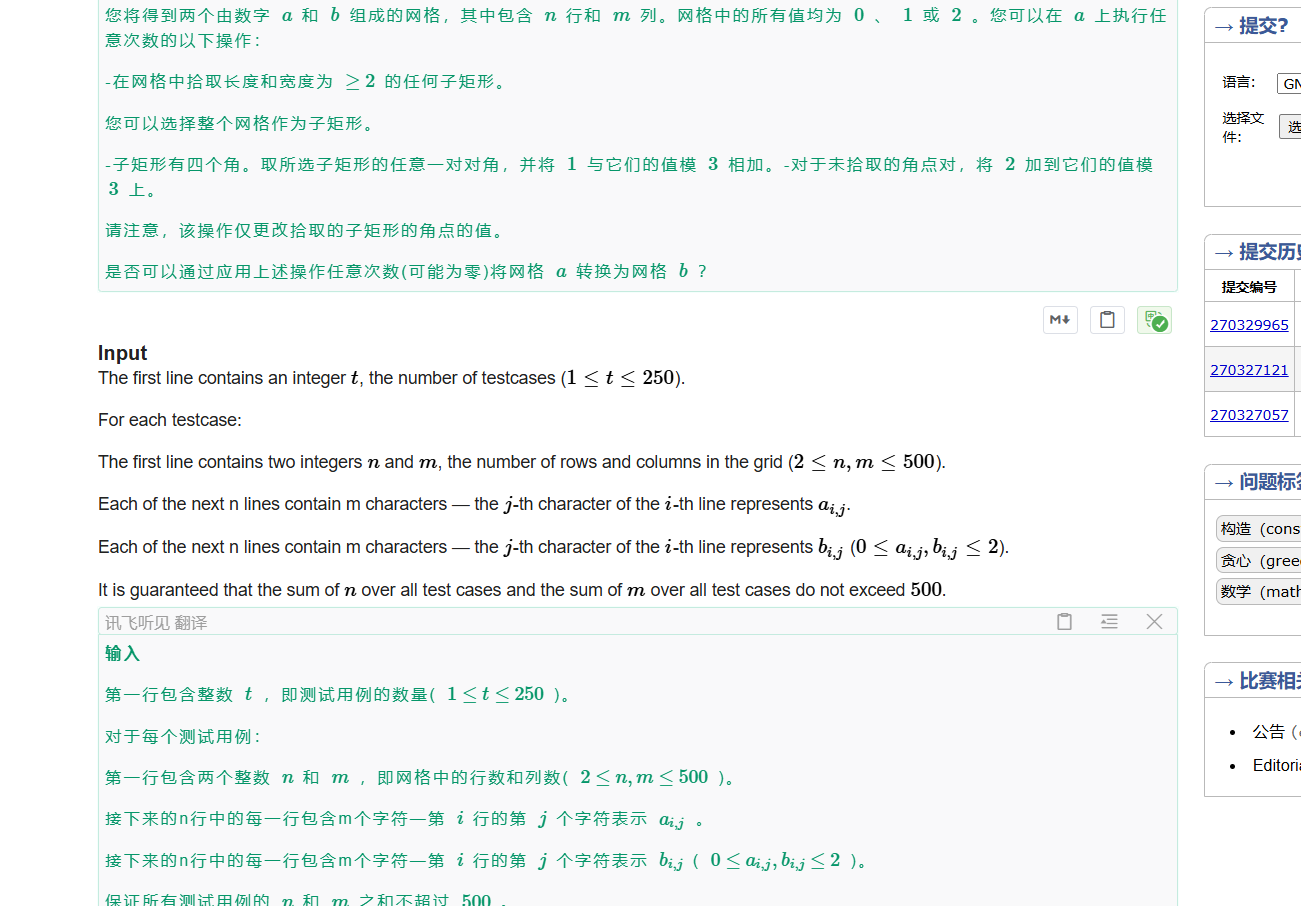
不擅长这种猜结论题，卡了很久

最后结论是每行每列的值模3不相等就不行

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=510;
char a[N][N];
char b[N][N];
int main()
{int t;cin>>t;while(t--){int n,m;cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++) cin>>a[i][j];}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++) cin>>b[i][j];}int jud=0;int c1=0,c2=0;for(int i=1;i<=n;i++){   c1=0,c2=0;for(int j=1;j<=m;j++){c1+=a[i][j]-'0';c2+=b[i][j]-'0';}if(c1%3!=c2%3) jud=1;}for(int i=1;i<=m;i++){   c1=0,c2=0;for(int j=1;j<=n;j++){c1+=a[j][i]-'0';c2+=b[j][i]-'0';}if(c1%3!=c2%3) jud=1;}if(jud==1) cout<<"NO"<<endl;else cout<<"YES"<<endl;}
}

C. Have Your Cake and Eat It Too

--------------------------------------题解---------------------------------------

这题我尝试了一个暴力解法，我求出了a,b,c三个数组的前缀和，然后枚举每个数组的前缀和中所有能放在中间的值假如说把数组a取得数字放在中间 让B，和C各自取左右两边的编号都试试如果符合条件就输出，不符合就继续试，直到把三个数组全试玩，如果没有符合条件的，就返回-1.略微考验码力

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
ll a[N];
ll b[N],c[N];
ll a1[N],b1[N],c1[N];
int main()
{int t;cin>>t;while(t--){ll n;cin>>n;ll sum=0;for(ll i=1;i<=n;i++) cin>>a[i],sum+=a[i];for(ll i=1;i<=n;i++) cin>>b[i];for(ll i=1;i<=n;i++) cin>>c[i];ll la=1,ra=1,lb=1,rb=1,lc=1,rc=1;ll s1=0;sum=sum/3+(sum%3!=0);a1[0]=b1[0]=c1[0]=0;for(ll i=1;i<=n;i++){  a1[i]=a1[i-1]+a[i];b1[i]=b1[i-1]+b[i];c1[i]=c1[i-1]+c[i];}ll jud=0;for(ll i=1;i<=n;i++){s1+=a[i];while(s1-a[la]>=sum){s1-=a[la];la++;}if(s1>=sum&&b1[la-1]>=sum&&c1[n]-c1[i]>=sum){cout<<la<<" "<<i<<" "<<1<<" "<<la-1<<" "<<i+1<<" "<<n<<'\n';jud=1;break;}if(s1>=sum&&c1[la-1]>=sum&&b1[n]-b1[i]>=sum){cout<<la<<" "<<i<<" "<<i+1<<" "<<n<<" "<<1<<" "<<la-1<<'\n';jud=1;break;}}s1=0;if(jud==0){for(ll i=1;i<=n;i++){s1+=b[i];while(s1-b[lb]>=sum){s1-=b[lb];lb++;}if(s1>=sum&&a1[lb-1]>=sum&&c1[n]-c1[i]>=sum){cout<<1<<" "<<lb-1<<" "<<lb<<" "<<i<<" "<<i+1<<" "<<n<<'\n';jud=1;break;}if(s1>=sum&&c1[lb-1]>=sum&&a1[n]-a1[i]>=sum){cout<<i+1<<" "<<n<<" "<<lb<<" "<<i<<" "<<1<<" "<<lb-1<<'\n';jud=1;break;}}}s1=0;if(jud==0){lb=1;//	cout<<11111<<endl;for(ll i=1;i<=n;i++){s1+=c[i];while(s1-c[lb]>=sum){s1-=c[lb];lb++;}if(s1>=sum&&a1[lb-1]>=sum&&b1[n]-b1[i]>=sum){cout<<1<<" "<<lb-1<<" "<<i+1<<" "<<n<<" "<<lb<<" "<<i<<'\n';jud=1;break;}if(s1>=sum&&b1[lb-1]>=sum&&a1[n]-a1[i]>=sum){cout<<i+1<<" "<<n<<" "<<1<<" "<<lb-1<<" "<<lb<<" "<<i<<'\n';jud=1;break;}}}if(jud==0) cout<<"-1"<<'\n';}}/*
4
4 4 4 4
4 4 4 4
4 4 4 4
*/

D

能看到这的都是糕手了，我简要分析

------------------------------题解-----------------------------------------------

每交换一次，数组中逆序对数量的奇偶性都会发生改变，因此我猜测这题是个猜结论的，因为我没分析出来。结论大概是和逆序对的奇偶性有关。

我们设定一个数组不变，只变一个数组，看看需要变多少次才能让两数组相同，看看需要奇数次还是偶数次，如果是偶数次便可以，奇数次不行
可以类比于两个人互相接近，一次只能走1，如果距离点是偶数便可以两人最后不能停在一个格子，奇数就可以

这里我写的不好看贴一下别人代码

点击查看代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
int a[200005], b[200005];
map<int, int> mp;
void solve()
{mp.clear();int n;cin >> n;for (int i=1;i<=n;i++) cin >> a[i];for (int i=1;i<=n;i++){cin >> b[i];mp[b[i]]=i;}int ans = 0;for (int i=1;i<=n;i++){if (b[i] == a[i]) continue;if (mp.count(a[i]) == 0){cout << "NO\n";return;}int p=mp[a[i]];swap(b[i],b[p]);mp[b[i]]=i;mp[b[p]]=p;ans+=1; }if (ans%2 == 0) cout << "YES\n";else cout << "NO\n";
}
signed main()
{int t;cin >> t;while (t--) solve();return 0;
}

**You can BE the best**