线性代数过滤的脏水

线性代数

向量

\(\to\)，信息学中用形如

\[\begin{bmatrix}a_1\\a_2\\\vdots\\a_p\end{bmatrix} \]

的矩阵来表示指向 \(\left(a_1,a_2,...,a_p\right)\) 的 \(p\) 维向量。

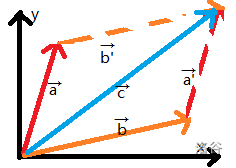
向量求和

直接就 \(\vec{a}+\vec{b}=\vec{c}\) 时满足 :

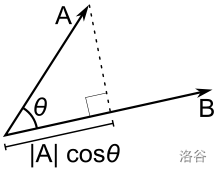
投影

借用8分钟带你彻底弄懂《线性代数》-CSDN博客的图

矩阵

出题人恶心人用的。分为列向量和行向量。

长这样：

\[\begin{pmatrix}a_{1,1}&\cdots&a_{1,m}\\\vdots&\ddots&\vdots\\a_{n,1}&\cdots&a_{n,m}\end{pmatrix} \]

矩阵加减法

设 \(A+B=C\)，\(A,B\) 是 \(m\times n\) 的矩阵，则 \(C_{i,j}=A_{i,j}+B_{i,j}\)。

\(A-B\) 同理。

易得：只有同型矩阵可进行相加或相减操作。

代码

//I am too lazy to write it.

矩阵乘法

点乘

信息学中涉及不多，拎出来讲一下：

设 \(A\cdot B=C\)，\(A,B\) 是 \(m\times n\) 的矩阵，则 \(C_{i,j}=A_{i,j}B_{i,j}\)。

或设 \(A\cdot B=C\)，\(A\) 是 \(1\times n\) 的矩阵，\(B\) 是 \(m\times n\) 的矩阵，则 \(C_{i,j}=A_{i}B_{i,j}\)。

显而易见的，点乘只能在 \(A,B\) 行数相同，列数相同或行数相同，\(A\) 只有 \(1\) 列的情况下进行。

叉乘

设 \(A\times B=C\)，其中 \(A\) 是 \(m\times g\) 的矩阵，\(B\) 是 \(g\times n\) 的矩阵，则 \(C_{i,j}=\sum^g_{k=1}A_{i,k}B_{k,j}\\\)。

易得：只有当 \(A\) 的行数与 \(B\) 的列数相等时 \(A\) 和 \(B\) 才可进行叉乘。

容（lan）易（de）证明，一般的矩阵叉乘不满足交换律，但满足结合律。

代码

点乘：

//懒得贴了

叉乘：

for(int k=1;k<=g;k++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)c[i][j]+=a[i][k]*b[k][j];

快速幂优化

就是说一堆 \(A\) 乘在一起就可以用矩阵快速幂。

代码（用的重载运算符）：

struct matrix{int a[MAXN][MAXN];matrix(){memset(a,0,sizeof(a));}matrix operator*(const matrix&b)const{matrix c;for(int k=1;k<=n;k++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)c.a[i][j]+=(a[i][k]*b.a[k][j])%mod,c.a[i][j]%=mod;return c;}
}a;
matrix qpow(matrix x,int y){matrix ans;for(int i=1;i<=n;i++)ans.a[i][i]=1;while(y){if(y&1)ans=ans*x;x=x*x,y>>=1;}return ans;
}

矩阵快速幂求斐波那契数列

不多赘述：初始矩阵 \(\begin{bmatrix}1&1\\0&0\end{bmatrix}\)，转移矩阵 \(\begin{bmatrix}1&1\\1&0\end{bmatrix}\)。

代码：

struct matrix{int a[2][2]={{0,0},{0,0}};matrix operator*(const matrix&b)const{matrix c;for(int k=0;k<2;k++)for(int i=0;i<2;i++)for(int j=0;j<2;j++)c.a[i][j]+=(a[i][k]*b.a[k][j])%mod,c.a[i][j]%=mod;return c;}inline void init(){a[0][0]=a[0][1]=a[1][0]=1;a[1][1]=0;}
}a;
inline matrix qpow(matrix x,int y){matrix ans;ans.a[0][0]=ans.a[0][1]=1; while(y){if(y&1)ans=ans*x;x=x*x,y>>=1;}return ans;
}
//求fib[n]输出a[0][0]即可.

高斯消元

高斯消元法（Gauss–Jordan elimination）是求解线性方程组的经典算法，它在当代数学中有着重要的地位和价值，是线性代数课程教学的重要组成部分——OIWiki

过程（包括异或高斯消元）

1. 将矩阵化为“倒三角”形式，即 Link。
2. 代入，回到 1，循序渐进求解。

代码

normal

for(int i=1;i<=n;i++)for(int j=1;j<=n+1;j++)cin>>a[i][j];
for(int i=1;i<=n;i++){int maxx=i;for(int j=1;j<=n;j++){if(fabs(a[j][j])>1e-7&&j<i)continue;if(fabs(a[j][i])>fabs(a[maxx][i]))maxx=j;}for(int j=1;j<=n+1;j++)swap(a[i][j],a[maxx][j]);if(fabs(a[i][i])<1e-7)continue;for(int j=n+1;j>=1;j--)a[i][j]/=a[i][i];for(int j=1;j<=n;j++){if(j!=i){double g=a[j][i]/a[i][i];for(int k=1;k<=n+1;k++)a[j][k]-=a[i][k]*g;}}
}

xor

bitset<1010>a[2010];
inline int gsxy(int n,int m){int t=-1;for(int i=1;i<=n;i++){int maxx=i;while(maxx<=m&&!a[maxx].test(i))maxx++;if(maxx>m)return -1;if(maxx!=i)swap(a[maxx],a[i]);for(int j=1;j<=m;j++)if(i!=j&&a[j].test(i))a[j]^=a[i];t=max(t,maxx);}return t;
}
//上面下面都是狗屎，上面是goshixiaoyuan，下面是Clay_L的goshimainfunction
for(int i=1;i<=m;i++){string str;bool v;cin>>str>>v;for(int j=0;j<n;j++)a[i].set(j+1,str[j]==49);a[i].set(0,v);
}
int ans=gsxy(n,m);