代码随想录day11 || 150 逆表达式求值 239 滑动窗口最大值 347 前k最高频元素

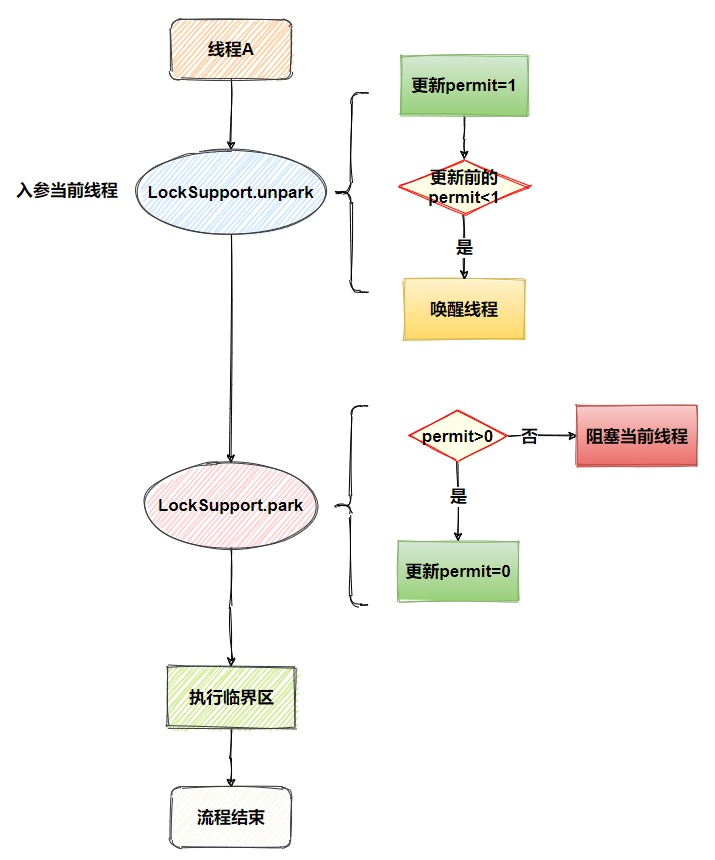
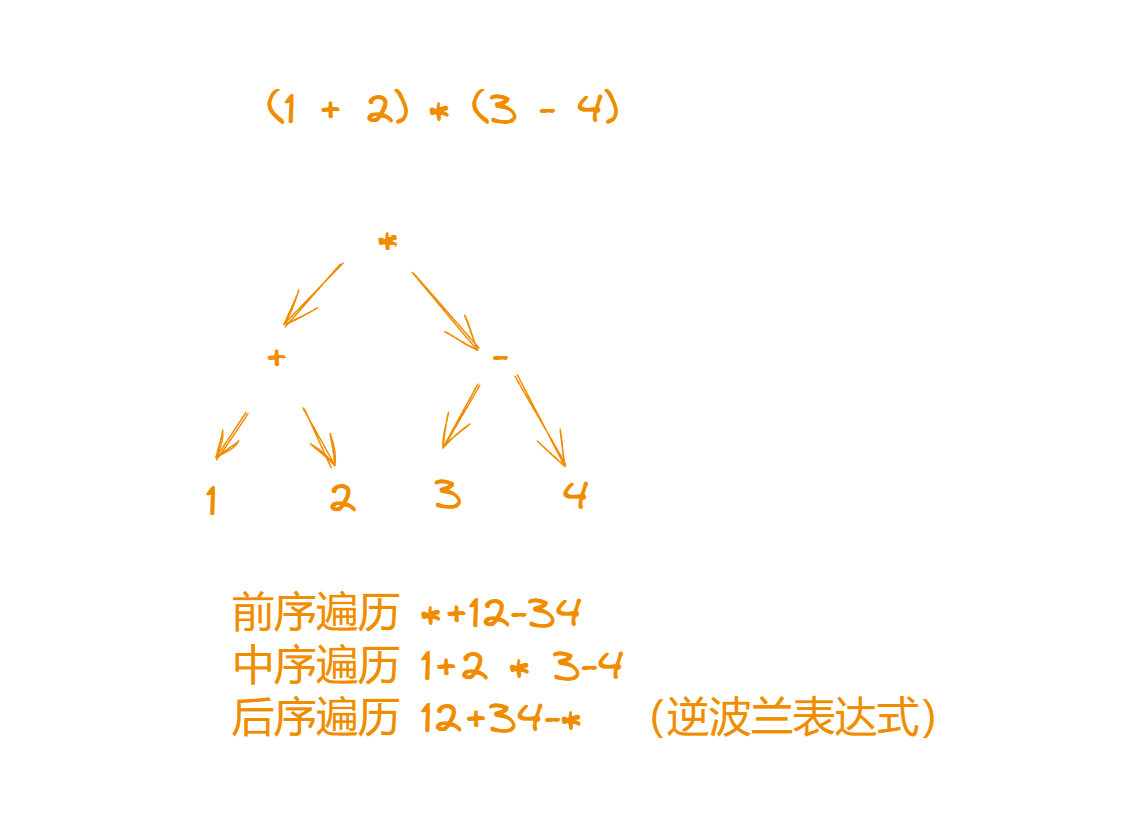
150 逆波兰表达式计算

func evalRPN(tokens []string) int {// 自己想是真的想不出来，看了视频之后有了思路// 本质上逻辑就是遇到数字入栈，遇到运算符号 出栈两个元素然后计算再入栈，最终就是计算结果stack := Constructor()for _, val := range tokens{// 如果数字入栈if isNum(val) {stack.Push(val)} else { // 此时遇到操作符号var v, v1, v2 intv1, _ = strconv.Atoi(stack.Pop())v2, _ = strconv.Atoi(stack.Pop())if val == "*" {v = v2 * v1}else if val == "/" {v = v2 / v1 // 先入的是前面的数，所以先出的是被除数v1}else if val == "-" {v = v2 - v1}else if val == "+" {v = v2 + v1}stack.Push(fmt.Sprintf("%d", v))}}res, _ := strconv.Atoi(stack.Pop())return res
}func isNum(s string) bool {_, err := strconv.Atoi(s)return err == nil
}type LinkNode struct{Data stringNext *LinkNodePrev *LinkNode
}type Stack struct {Node *LinkNode // 存储尾节点Size int
}func Constructor() *Stack {return &Stack{Node: &LinkNode{},Size: 0,}
}func (s *Stack) Push(str string) {node := &LinkNode{str, nil, s.Node}s.Node.Next = nodes.Node = nodes.Size++
}func (s *Stack) Pop() string {temp := s.Node// 断开节点s.Node = s.Node.Prevs.Node.Next = niltemp.Prev = nils.Size--return temp.Data
}func (s *Stack) Top() string {return s.Node.Data
}func (s *Stack) Empty() bool {return s.Size == 0
}// 时间 遍历一遍n*stack.Push 1 = n  空间 n 

239 滑动窗口最大值

func maxSlidingWindow(nums []int, k int) []int {// 思考，遍历一次var res  []intfor i:=0; i+k <= len(nums); i++ {res = append(res, max(nums[i: i+k]))}return res
}func max(li []int) int {max := math.MinIntfor _, v := range li{if v > max {max = v}}return max
}
// 暴力求解会超时

func maxSlidingWindow(nums []int, k int) []int {// 思考，遍历一次, 每次都重新计算最大值// 优化思路2: 不每次都一一便利求值，而是对比去除元素以及新元素，如果去除元素是最大值，重新求最大值，如果非最大值并且新元素大于最大值，保存var (res  []inttemp, m int)res = append(res, max(nums[0: 0+k]))temp = nums[0]for i:=1; i+k <= len(nums); i++ {// 判断删除值是不是上一次最大值fmt.Println(i, temp, res[i-1], nums[i+k-1])if temp == res[i-1] {m = max(nums[i: i+k]) // 上一次最大值被删除，要重新计算} else if nums[i+k-1] > res[i-1] { // 上一个窗口最大值没有被删除，且新加入值大于上一次最大m = nums[i+k-1]} else { // 最大没被删除，并且新加入也小于最大m = res[i-1]}res = append(res, m)temp = nums[i] // 下一次滑动要删除的值}return res
}// 小优化之后还是会超时

func maxSlidingWindow(nums []int, k int) []int {// 思考，遍历一次, 每次都重新计算最大值// 优化思路2: 不每次都一一便利求值，而是对比去除元素以及新元素，如果去除元素是最大值，重新求最大值，如果非最大值并且新元素大于最大值，保存var (q *Queueres []int)q = Constructor()res = make([]int, len(nums)-k+1)// 塞入前k个元素入队for i:=0; i<k; i++{q.Pushn(nums[i])}res[0] = q.Top()for i:=1; i+k-1 < len(nums); i++{q.Popn(nums[i-1])q.Pushn(nums[i+k-1])fmt.Println(q.Data)res[i] = q.Top()}return res
}// 单调队列
type Queue struct{Data []intSize int
}func Constructor() *Queue{return &Queue{}
}func (q *Queue) Push(n int) {q.Data = append(q.Data, n)q.Size++
}func (q *Queue) Pop() {if q.Size == 0 {return}q.Data = q.Data[1:]q.Size--return
}func (q *Queue) PopEnd() {if q.Size == 0{return}q.Size--q.Data = q.Data[:q.Size]return
}func (q *Queue) Top() int {if q.Size == 0{return 0}return q.Data[0]
}func (q *Queue) Empty() bool {return q.Size == 0
}func (q *Queue) Popn(n int) {// 判断弹出元素是不是队列首位，如果是则弹出，如果不是那么就不操作if q.Size == 0 || q.Top() != n {return}q.Pop() // 弹出首位元素
}func (q *Queue) Pushn(n int) {// 如果加入元素大于末尾元素，那么循环弹出末尾元素，反之正常加入for q.Size > 0 && n > q.Data[q.Size-1] {q.PopEnd() // 弹出小于n的所有末尾元素}q.Push(n)  // 插入到末尾}// 麻了还是超时

// tmd 必须双端队列，自己实现的队列复杂度高还是超时//leetcode submit region begin(Prohibit modification and deletion)
func maxSlidingWindow(nums []int, k int) []int {// 思考，遍历一次, 每次都重新计算最大值// 优化思路2: 不每次都一一便利求值，而是对比去除元素以及新元素，如果去除元素是最大值，重新求最大值，如果非最大值并且新元素大于最大值，保存if len(nums) == 0 || k == 0 {return []int{}}var res []intdeque := []int{}for i := 0; i < len(nums); i++ {// 移除窗口外的元素if len(deque) > 0 && deque[0] < i-k+1 {deque = deque[1:]}// 移除小于当前元素的所有元素for len(deque) > 0 && nums[deque[len(deque)-1]] < nums[i] {deque = deque[:len(deque)-1]}// 将当前元素添加到双端队列deque = append(deque, i)// 队列的第一个元素是当前窗口的最大值if i >= k-1 {res = append(res, nums[deque[0]])}}return res
}
时间 n 空间 n

347 前k高频元素

func topKFrequent(nums []int, k int) []int {// 暴力法，将出现次数存储到map，然后对map结果进行排序，最后拿出排序后前n keyvar m = make(map[int]int)for _, v := range nums{m[v]++}var li []intfor _, v := range m{li = append(li, v)  // 次数数组}li = quick_sort(li)var res = make([]int, k)for i := 0; i < k; i++{for k, v := range m {//fmt.Println(m)if v == li[i] {res[i] = kdelete(m, k)break}}}return res
}func quick_sort(nums []int) []int{// 快排，左边小于v，右边大于v// 插排，维护两个数组，左边小于右边大于if len(nums) == 0 {return nums}idx := nums[0]var left, right []intfor i:=1; i<len(nums); i++{if nums[i] > idx{left = append(left, nums[i])} else {right = append(right, nums[i])}}return append(quick_sort(left), append([]int{idx}, quick_sort(right)...)...)
}// 暴力方法通过测试
// 空间是n，因为最坏情况，每个元素都不相同创建长度为n的map和次数数组，时间复杂度插入map n + 插入数组 n + 快排nlogn + 外层常数次数遍历k内层最坏n次遍历 = n*logn

堆（Heap）

堆是一种特殊的树状数据结构，它满足堆属性（heap property），可以用来高效地实现优先队列。堆分为两种主要类型：最大堆（max-heap）和最小堆（min-heap）。

最大堆（Max-Heap）

在最大堆中，每个节点的值都大于或等于其子节点的值。换句话说，根节点的值是整个堆中最大的。

最小堆（Min-Heap）

在最小堆中，每个节点的值都小于或等于其子节点的值。换句话说，根节点的值是整个堆中最小的。

堆的性质

1. 完全二叉树: 堆是一棵完全二叉树（Complete Binary Tree），即除了最后一层，其他层都是满的，最后一层的节点都靠左排列。
2. 堆属性: 最大堆中每个节点的值都大于或等于其子节点的值，最小堆中每个节点的值都小于或等于其子节点的值。

堆的操作

堆的常见操作包括插入、删除和取顶元素。以下是这些操作的详细描述：

1. 插入（Insert）:

   • 将新元素添加到堆的末尾，然后向上调整（上滤）以保持堆的性质。
   • 时间复杂度：(O(log n))，其中 (n) 是堆的大小。

2. 删除（Delete）:

   • 通常是删除堆顶元素（最大堆的最大值或最小堆的最小值）。将堆的最后一个元素移到堆顶，然后向下调整（下滤）以保持堆的性质。
   • 时间复杂度：(O(log n))。

3. 取顶元素（Peek）:

   • 直接返回堆顶元素（最大堆的最大值或最小堆的最小值）。
   • 时间复杂度：(O(1))。

堆的实现

堆通常使用数组来实现，利用数组下标来表示树的结构。对于一个节点在数组中的位置 (i)：

• 左子节点的位置是 (2i + 1)
• 右子节点的位置是 (2i + 2)
• 父节点的位置是 (（ i - 1 ）/2)

Go 语言中的堆

Go 语言标准库中提供了 container/heap 包来实现堆。heap 是一个接口类型，任何实现了 heap.Interface 接口的类型都可以被视为一个堆。这个接口定义在 Go 语言的 container/heap 包中。

heap.Interface 接口

heap.Interface 接口定义如下：

type Interface interface {sort.InterfacePush(x interface{}) // 添加元素到堆中Pop() interface{}   // 删除堆顶元素并返回
}

sort.Interface 接口定义了以下三个方法：

type Interface interface {Len() int           // 返回堆的元素数量Less(i, j int) bool // 比较索引为 i 和 j 的元素Swap(i, j int)      // 交换索引为 i 和 j 的元素
}

因此，任何实现了 Len、Less、Swap、Push 和 Pop 方法的类型都可以使用 heap 包中的函数。

// 写小顶堆中的收获1，值类型接收者和指针类型接收者
type li []intfunc (l li) swap(i, j int) {return l[i], l[j] = l[j], l[i]}
func (l *li) swap(i, j int) {return l[i], l[j] = l[j], l[i]}
这两种写法都是正确的，为什么呢？
因为切片、映射、通道和接口是引用类型。即使使用值接收者，这些类型的方法内部对它们的元素或内容的修改会反映到原始变量中。这是因为这些引用类型的值包含指向底层数据结构的指针。2，append 操作的是值类型
func (l *li) Push(x int) {*l = append(*l, x)}直接思考可能就写成l = append(l, x) ，但是这样编译错误，因为l本身是指针类型，append操作的是值类型，所以要对l取值*l

//leetcode submit region begin(Prohibit modification and deletion)
func topKFrequent(nums []int, k int) []int {// 暴力法，将出现次数存储到map，然后对map结果进行排序，最后拿出排序后前n keyvar m = make(map[int]int)for _, v := range nums{m[v]++}var mh = &MinHeap{}heap.Init(mh)for _, v := range m {heap.Push(mh, v)// 入堆if mh.Len() > k { // 达到最大规模，弹出堆顶最小元素heap.Pop(mh)}}fmt.Println(m, mh)var res = make([]int, k)for i := 0; i < k; i++{data := heap.Pop(mh)for k, v := range m {//fmt.Println(m)if data == v {res[i] = kdelete(m, k)break}}}return res
}// 定义小顶堆
type MinHeap []int// heap类型本质上是接口，所有实现了less swap len pop push方法的类型都可以认为是heap，因为实现了heap接口
func (h *MinHeap) Less(i, j int) bool  {return (*h)[i] < (*h)[j]
}func (h *MinHeap) Len() int {return len(*h)
}func (h *MinHeap) Swap(i, j int) {(*h)[i], (*h)[j] = (*h)[j], (*h)[i]
}func (h *MinHeap) Pop() any {// heap.Pop 会先交换堆顶和末尾，然后格式化前n-1元素，最后调用本方法，实现弹出堆顶li := *hnum := li[len(li)-1]*h = li[:len(li)-1]return num
}func (h *MinHeap) Push(x any) {// heap.Push 先调用本方法，然后再进行堆格式化，重新修正数组，所以可以直接append*h = append(*h, x.(int))
}时间复杂度取决于堆 nLogk  空间 n