闲了好久的wym复活拉~更个辣鸡的线段树
如果你不知道什么是线段树这个就不用看
由于我们平时可能会遇到一些恶心的题叫做给你 \(10^5\) 个数的数组,然后 \(10^5\) 次修改或查询,这样显然暴力是可以做的而且ST表我们无视修改。这个时候可以用线段树、树状数组或者其他大佬们的神仙算法,由于我不知道何谓lowbit所以用的线段树。
线段树的空间是树状数组的4倍,或者某些例外,8倍,即 \(4N\) 或 \(8N\)。
线段树的好处在于它的功能比树状数组多,最重要的在于,树状数组维护的是前缀和,所以不能维护最大最小值。而线段树维护的是实实在在的区间和,所以树状数组能做到的,线段树都能做到。但是线段树的时空复杂度都比树状数组高,而且代码更复杂。有些 \(N=5 \times 10^6\) 的题就不能用线段树做了。
好了瞎扯完了,现在来看线段树的思想是什么。
看图(图中线段树维护的是区间和):
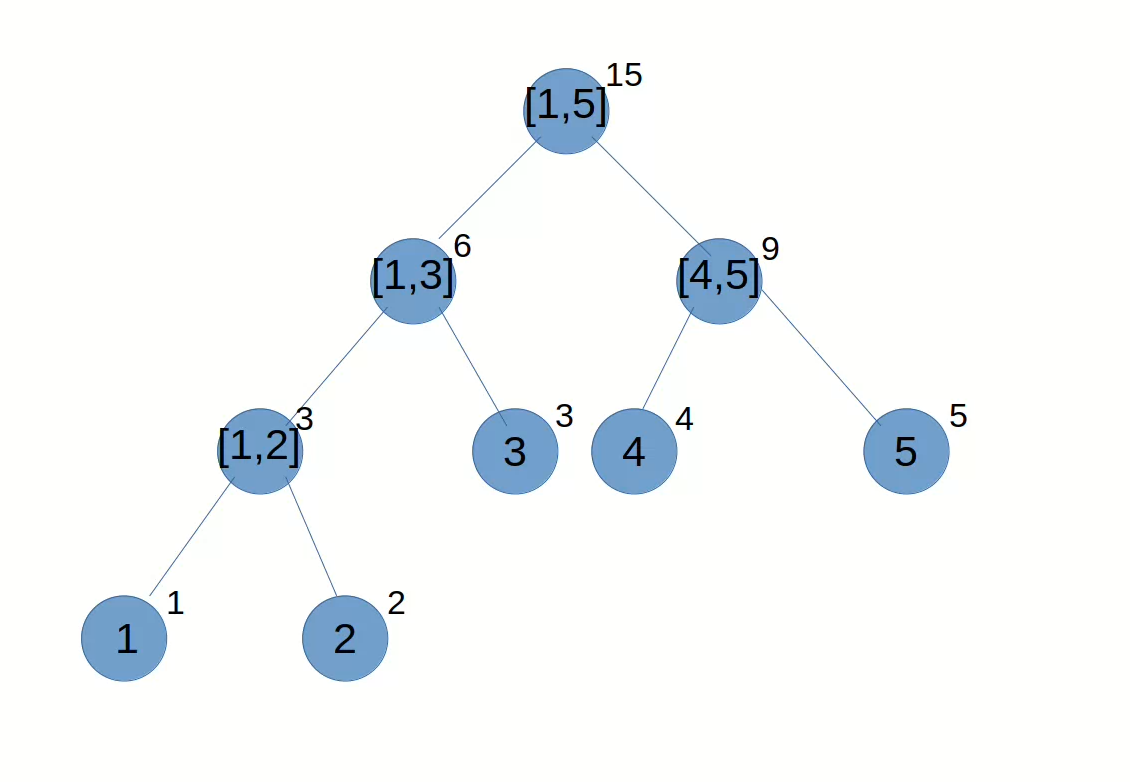
由图可以得出,首先,线段树是一个二叉堆,或者叫作完全二叉树,而且树中每个点对应数组中的一个区间。这样方便的地方在于,我查询一个区间的时候,如果恰好遇到一个查询区间包含的区间时,就能直接取值了。
题目给出一个数组,首先我们要建出这个线段树。
const int N=1e5+10;
int n,a[N],t[N*4]; //a数组是输入的,t数组用来存储线段树,根为1,一个节点 i 的左子节点为 2i,右子节点为 2i+1
void build(int now,int tl,int tr){ //now表示线段树的节点,tl和tr表示原数组的区间if(tl==tr){ //遇到一个原数组的数(区间长度为1),即线段树中的叶子节点了t[now]=a[tl]; //或a[tr]return ;}int mid=(tl+tr)/2; //区分左子树和右子树build(now*2,tl,mid); //递归建左子树build(now*2+1,mid+1,tr); //递归建右子树t[now]=t[now*2]+t[now*2+1]; //区间和,或者可以定义其他操作,注意这里一定不要忘写
}
可以输出测试一下,以上图为例:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,a[N],t[N*4];
int flag[N];
void build(int now,int tl,int tr){if(tl==tr){flag[now]=1;t[now]=a[tl];return ;}int mid=(tl+tr)/2;build(now*2,tl,mid);build(now*2+1,mid+1,tr);t[now]=t[now*2]+t[now*2+1];flag[now]=1;
}
int main(){n=5;a[1]=1,a[2]=2,a[3]=3,a[4]=4,a[5]=5;build(1,1,n);for(int i=1;i<=n*4;i++){if(flag[i]){cout<<t[i]<<" ";}}return 0;
}
输出结果:
15 6 9 3 3 4 5 1 2
相当于原图片中树的层次遍历。你也可以写一个dfs求前序/中序/后序遍历。或者也可以用dfs/bfs求树中每个点代表的区间或数。甚至,你可以用bfs写build。
很明显,build函数时间复杂度 \(O(n)\)。
现在树建好了,我们先讲查询,再讲修改。
单点查询:跟build类似,但略有不同。自己思考一下为什么tl==tr不需要再判断tl==pos或tr==pos。
int query(int now,int tl,int tr,int pos){ //pos代表查询的数组下标if(tl>pos||tr<pos){ //不在范围内return 0;}if(tl==tr){ //找到了return t[now];}int mid=(tl+tr)/2;return query(now*2,tl,mid,pos)+query(now*2+1,mid+1,tr,pos);
}
区间查询:这个时候,t数组中非叶子的节点,即代表原数组中区间的部分就派上用场了。查询时,如果发现了一个查询范围包含的区间,就可以直接取走了。否则,把目前的区间分成两半,然后递归去找。

比如我们要查询区间 \([2,5]\) 的和。
\([1,5]\) 不完全属于 \([2,5]\),分成 \([1,3]\) 和 \([4,5]\)。
\([1,3]\) 不完全属于 \([2,5]\)。分成 \([1,2]\) 和 \([3,3]\)。
\([1,2]\) 不完全属于 \([2,5]\)。分成 \([1,1]\) 和 \([2,2]\)。
\([1,1]\) 不属于 \([2,5]\)。返回 \(0\)。
\([2,2]\) 属于 \([2,5]\)。返回 \(t\) 数组中 \([2,2]\) 对应的 \(2\)。
\([1,2]\) 收到返回值 \(0\) 和 \(2\)。相加得到 \(2\)。\([1,2]\) 返回 \(2\)。
\([3,3]\) 属于 \([2,5]\)。返回 \(t\) 数组中 \([3,3]\) 对应的 \(3\)。
\([1,3]\) 收到返回值 \(2\) 和 \(3\)。相加得到 \(5\)。\([1,3]\) 返回 \(5\)。
\([4,5]\) 属于 \([4,5]\)。返回 \(t\) 数组中 \([4,5]\) 对应的 \(9\)。
\([1,5]\) 收到返回值 \(5\) 和 \(9\)。相加得到 \(14\)。查询函数结束,函数返回值 \(14\)。
看似复杂,只要画个图,就明白了。自己尝试一下吧。可以结合代码。
int query(int now,int tl,int tr,int l,int r){ //l和r表示查询的区间if(tl>=l&&tr<=r){ //[tl,tr]完全属于[l,r]return t[now];}if(tl>r||tr<l){ //[tl,tr]不再[l,r]范围内return 0;}int mid=(tl+tr)/2; //不完全属于return query(now*2,tl,mid,l,r)+query(now*2+1,mid+1,tr,l,r);
}
自己运行试一下,也可以自己修改代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,a[N],t[N*4];
void build(int now,int tl,int tr){if(tl==tr){t[now]=a[tl];return ;}int mid=(tl+tr)/2;build(now*2,tl,mid);build(now*2+1,mid+1,tr);t[now]=t[now*2]+t[now*2+1];
}
int query(int now,int tl,int tr,int l,int r){if(tl>=l&&tr<=r){return t[now];}if(tl>r||tr<l){return 0;}int mid=(tl+tr)/2;return query(now*2,tl,mid,l,r)+query(now*2+1,mid+1,tr,l,r);
}
int main(){n=5;a[1]=1,a[2]=2,a[3]=3,a[4]=4,a[5]=5;build(1,1,n);cout<<query(1,1,n,2,5);return 0;
}
单点修改:其实和build还是区别不大。你可以尝试自己理解。通常情况下会是区间增加。
void modify(int now,int tl,int tr,int pos,int x){ //修改数组中下标为pos的数为xif(tl>pos||tr<pos){ //不在范围内return ;}if(tl==tr){ //这个点就是要修改的点t[now]=x;return ;}int mid=(tl+tr)/2;modify(now*2,tl,mid,pos,x);modify(now*2+1,mid+1,tr,pos,x);t[now]=t[now*2]+t[now*2+1]; //这个地方不能忘,修改之后要更新所有祖先的值
}
结合区间查询的代码(可以自行修改):
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,a[N],t[N*4];
void build(int now,int tl,int tr){if(tl==tr){t[now]=a[tl];return ;}int mid=(tl+tr)/2;build(now*2,tl,mid);build(now*2+1,mid+1,tr);t[now]=t[now*2]+t[now*2+1];
}
int query(int now,int tl,int tr,int l,int r){if(tl>=l&&tr<=r){return t[now];}if(tl>r||tr<l){return 0;}int mid=(tl+tr)/2;return query(now*2,tl,mid,l,r)+query(now*2+1,mid+1,tr,l,r);
}
void modify(int now,int tl,int tr,int pos,int x){if(tl>pos||tr<pos){return ;}if(tl==tr){t[now]=x;return ;}int mid=(tl+tr)/2;modify(now*2,tl,mid,pos,x);modify(now*2+1,mid+1,tr,pos,x);t[now]=t[now*2]+t[now*2+1];
}
int main(){n=5;a[1]=1,a[2]=2,a[3]=3,a[4]=4,a[5]=5;build(1,1,n);modify(1,1,n,4,5);cout<<query(1,1,n,2,5);return 0;
}
以上所有操作的时间复杂度都是 \(O(\log n)\) 的。对于单点查询,最多会查到数中最深的点,而一棵完全二叉树的深度大概时 \(\log n\) 左右。对于区间查询和单点修改,同理。进行区间操作时,会及时停止递归(当某子树不在查询范围内时),实际上递归的次数是低于 \(\log n\) 的,可以自己举几个例子试试看。
区间增加,可以把区间每个数都单独单点修改一次,但这样会变成 \(O(n \log n)\),\(n\) 次区间修改就是 \(O(n^2 \log n)\)。这块内容下次再讲,我们先看例题,练习一下基础。
习题
第一题
模板题。记得开long long。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e5+10;
ll n,m,t[N*4];
ll query(ll now,ll tl,ll tr,ll l,ll r){if(tl>=l&&tr<=r){return t[now];}if(tl>r||tr<l){return 0;}ll mid=(tl+tr)/2;return query(now*2,tl,mid,l,r)+query(now*2+1,mid+1,tr,l,r);
}
void add(ll now,ll tl,ll tr,ll pos,ll x){if(tl>pos||tr<pos){return ;}if(tl==tr){t[now]+=x;return ;}ll mid=(tl+tr)/2;add(now*2,tl,mid,pos,x);add(now*2+1,mid+1,tr,pos,x);t[now]=t[now*2]+t[now*2+1];
}
int main(){//freopen("xx.in","r",stdin);//freopen("xx.out","w",stdout);ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m;for(ll i=1;i<=m;i++){ll k,a,b;cin>>k>>a>>b;if(k){cout<<query(1,1,n,a,b)<<"\n";}else{add(1,1,n,a,b);}}return 0;
}
第二题
这道题有点挑战。看似没法通过时间限制,但是这道题的操作是平方根,\(10^{12}\) 开 \(6\) 次平方根就是 \(1\) 了。所以在修改的时候,如果发现一个子树都是 \(1\),就不用修改了,因为 \(1\) 的平方根还是 \(1\)。否则,只能一直递归,直到叶子节点,再把它取平方根。记得t[now]=t[now*2]+t[now*2+1]。判定子树都为 \(1\) 的方法很多,你可以看看子树的和是否等于子树大大小,或者专门再写一个线段树维护是否都是 \(1\)。这道题思路懂了,就好写了。有坑,注意 \(l\) 可能大于 \(r\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e5+10;
ll n,m,a[N],t[N*8];
void build(ll now,ll tl,ll tr){if(tl==tr){t[now]=a[tl];return ;}int mid=(tl+tr)/2;build(now*2,tl,mid);build(now*2+1,mid+1,tr);t[now]=t[now*2]+t[now*2+1];
}
ll query(ll now,ll tl,ll tr,ll l,ll r){if(tl>=l&&tr<=r){return t[now];}if(tl>r||tr<l){return 0;}ll mid=(tl+tr)/2;return query(now*2,tl,mid,l,r)+query(now*2+1,mid+1,tr,l,r);
}
void modify(ll now,ll tl,ll tr,ll l,ll r){if(tl>r||tr<l){return ;}if(tl==tr){t[now]=sqrt(t[now]);return ;}ll mid=(tl+tr)/2;if(t[now*2]!=mid-tl+1){modify(now*2,tl,mid,l,r);}if(t[now*2+1]!=tr-mid){modify(now*2+1,mid+1,tr,l,r);}t[now]=t[now*2]+t[now*2+1];
}
int main(){//freopen("xx.in","r",stdin);//freopen("xx.out","w",stdout);ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;for(ll i=1;i<=n;i++){cin>>a[i];}build(1,1,n);cin>>m;for(ll i=1;i<=m;i++){ll k,l,r;cin>>k>>l>>r;if(l>r){swap(l,r);}if(k){cout<<query(1,1,n,l,r)<<"\n";}else{modify(1,1,n,l,r);}}return 0;
}
如果这道题你是不看题解代码AC的,证明你对线段树的最基础的部分已经足够熟悉了。但是线段树的的基本操作比这个难,加油吧~