【NOIP模拟一】20240729
C
注意到答案是s除以区间gcd。
裴蜀定理推广
D
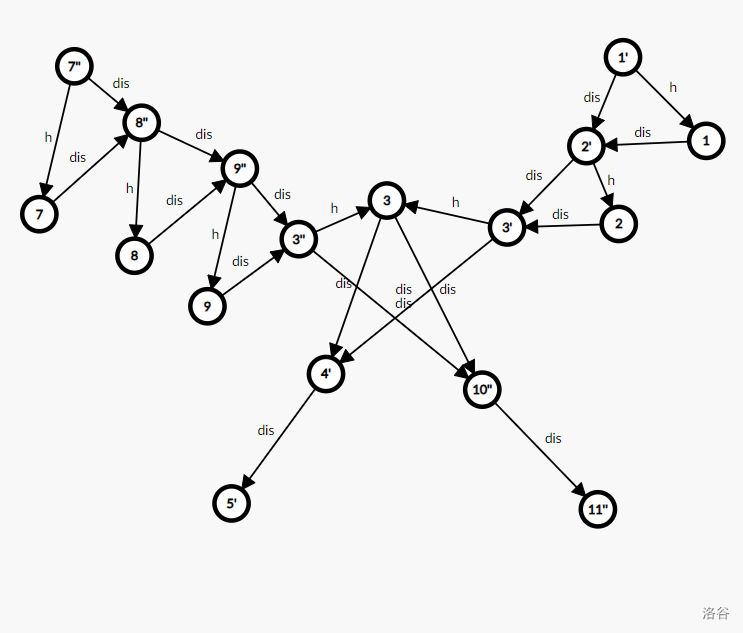
像这样建图,跑全源最短路。
在这张图上有 \(1\to 2\to 3\to 4\to 5\) 和 \(7\to 8\to 9\to 3\ to 10\ to 11\) 两条路径。把路径上的点看作车上的点,每个点本身看作车站。
可以发现在车(一条路径)上的点可以选择是否停靠也就是执行了边权为 \(-dist + \max(0,h_i)\) 这一操作。而如果要换乘,即 \(2\to 3\to 10\) 这样的操作则不得不取 \(h_i\)。
然后跑全源最短路,注意一些细节即可。(因为这道题有三角形不等式等奇葩性质,SPFA 是可以的)。具体建边操作可以看代码。
#include <bits/stdc++.h>
using namespace std;
#define il inline
#define ptc putchar
#define reg register
#define pb push_back
#define R(i, l, r) for (int i = l; i <= r; ++i)
#define debug puts("--------------------------------------------")
typedef long long ll;
typedef pair<int, int> PII;
namespace ZeroTwo {template <typename T>il void read(T &x) { x = 0; T f = 1; char ch;while (!isdigit(ch = getchar())) f -= (ch == '-') << 1;while (isdigit(ch)) x = (x << 1) + (x << 3) + (ch & 15), ch = getchar();x *= f;}template <typename T, typename ...L>il void read(T &x, L &...y) {read(x); read(y...);}template <typename T>il void write(T x) {if (x < 0) ptc('-'), x = -x;if (x > 9) write(x / 10);ptc(x % 10 + '0');}template <typename T, typename ...L>il void write(T &x, L &...y) {write(x), ptc(' '); write(y...);}
}
using namespace ZeroTwo;
#define int ll
const int N = 8005;
int n, m;
struct node {int x, y, v;
} a[2005];
ll calc(int i, int j) {ll s = 1ll * (a[i].x - a[j].x) * (a[i].x - a[j].x) + (a[i].y - a[j].y) * (a[i].y - a[j].y);return ceil(sqrt(s));
}
bool vis[N + 6000];
ll dis[N + 6000];
vector <pair <int, ll> > E[N + 6000];
int tot;
void SPFA(int s) {queue <int> q; q.push(s);R(i, 1, tot) vis[i] = 0, dis[i] = -1e15; vis[s] = 1; dis[s] = 0;while (q.size()) {int x = q.front(); q.pop();vis[x] = 0;for (auto [v, w] : E[x]) {if (dis[v] < dis[x] + w) {dis[v] = dis[x] + w;if (!vis[v]) {vis[v] = 1;q.push(v);}}}}
}
int idx[N][N];
int id(int i, int x) {if (!idx[i][x]) idx[i][x] = ++tot;return idx[i][x];
}
int b[N];
void add(int u, int v, int w) {E[u].push_back({v, w});
}
signed main() {freopen("metro.in", "r", stdin);freopen("metro.out", "w", stdout);read(n, m);R(i, 1, n) read(a[i].x, a[i].y, a[i].v);tot = n;R(t, 1, m) {int k; read(k);R(i, 1, k) read(b[i]);R(i, 1, k - 1) {int d = -calc(b[i], b[i + 1]);add(id(t, b[i]), b[i], a[b[i]].v);add(b[i], id(t, b[i + 1]), d);add(id(t, b[i]), id(t, b[i + 1]), d);}add(id(t, b[k]), b[k], a[b[k]].v);}R(i, 1, n) {SPFA(i);R(j, 1, n) printf("%lld ", dis[j] + a[i].v);ptc('\n');}return 0;
}