线性丢番图方程

线性丢番图方程定理

设 \(a,b\) 是整数且 \(gcd(a,b) = d\). 如果 \(d\) 不能整除 \(c\) , 那么方程 \(ax+by=c\) 没有整数解, 如果\(d\) 可以整除 \(c\), 则存在无穷个解. 另外, 如果 \((x_0,y_0)\) 是方程的一个特解, 那么所有解都可以表示为 :

\[x = x_0 + (\frac{b}{d})n, y = y_0 - (\frac{a}{d})n \]

即: \(ax+by=c\) 有解的充分必要条件是 \(d = gcd(a,b)|c\)
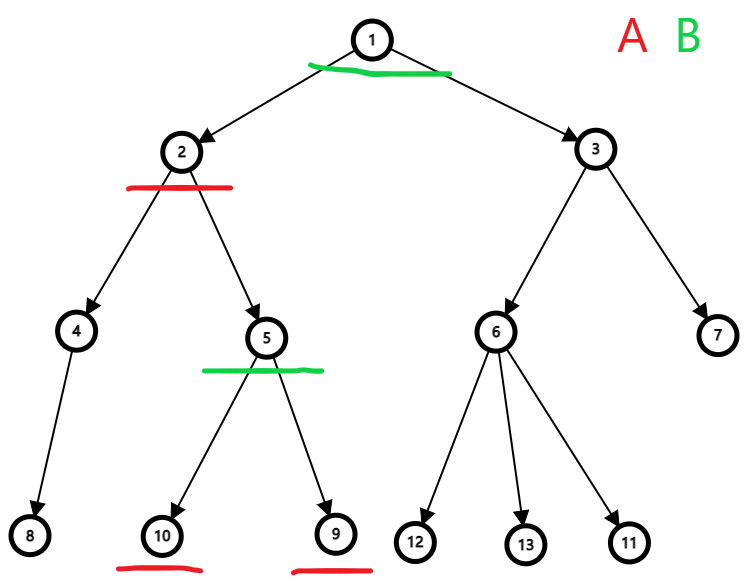
可借助如下图进行理解

扩展欧几里得算法与线性丢番图的解

求解 \(ax+by=c\) 的主要是找到一个特解, 那么 \(exgcd\) 的作用就是找到一个特解
其扩展欧几里得算法如下:

int exgcd(int a, int b, int &x, int &y){    if(b == 0){        x = 1, y = 0;        return a;    }    int d = exgcd(b, a % b, y, x);       y -= a / b * x;    return d;};

有时为了简化描述, 把 \(ax + by = gcd(a,b)\) 两边除以 \(gcd(a,b)\), 得到 \(cx + dy = 1\), 其中 \(c = \frac{a}{gcd(a,b)}\), \(d = \frac{b}{gcd(a,b)}\). \(c\) 与 \(d\) 是互素的, 则 \(cx + dy = 1\) 的通解为 \(x = x_0 + dn\), \(y = y_0 -cn\)
具体步骤如下:

例题: P1516 青蛙的约会 - 洛谷

#include <bits/stdc++.h>#define int long longusing namespace std;const int N = 1e6 + 10, mod = 1e9 + 7;int exgcd(int a, int b, int &x, int &y){    if(b == 0){        x = 1, y = 0;        return a;    }    int d = exgcd(b, a % b, y, x);       y -= a / b * x;    return d;};signed main(){    std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);    int n, m, x, y, L; cin >> x >> y >> m >> n >> L;    int a = n - m, b = L, c = x - y;    if(a < 0) a = -a, c = -c;    int d = exgcd(a, b, x, y);    if(c % d != 0) cout << "Impossible" << '\n';    else cout << ((x * (c / d)) % (L / d) + (L / d)) % (L / d) << '\n';    return 0;}
```![](https://img2024.cnblogs.com/blog/3205031/202408/3205031-20240806202623129-592127437.png)