【题解】ABC365（A~E）

前四题30min切，然后T5死磕70min+几发小唐错，距离比赛结束还有16s交最后一发，AC了。

目录

• A. Leap Year
  • 题目描述
  • 思路
  • 代码
• B. Second Best
  • 题目描述
  • 思路
  • 代码
• C. Transportation Expenses
  • 题目描述
  • 思路
  • 代码
• D. AtCoder Janken 3
  • 题目描述
  • 思路
  • 代码
• E. Xor Sigma Problem
  • 题目描述
  • 思路
  • 代码

A. Leap Year

题目描述

给你一个年份 \(Y\)，输出该年的天数（判断闰年），\(1583\le Y\le2023\)。

思路

直接模拟即可。不能整除 \(4\) 或整除 \(4\) 且整除 \(100\) 的输出 \(365\)，其余的输出 \(366\)。复杂度 \(O(1)\)。

代码

#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register
#define inf 0x3f3f3f3f
int a;
int main()
{scanf("%d",&a);if(a%4!=0||(a%100==0&&a%400!=0)) {puts("365");}else{puts("366");}return 0;
}

B. Second Best

题目描述

给你一个长为 \(N\) 的序列 \(A\)，输出这个序列的次大值。\(2\le N\le100\)，\(1\le A_i\le10^9\)。

思路

数据范围很小，显然复杂度 \(O(n\log n)\) 可解。用排序或者优先队列都可以。赛时为了方便，打的是优先队列。

代码

#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a,b;
priority_queue<pair<int,int>>que;
int main()
{scanf("%d",&a);for(ri i=1;i<=a;i++){scanf("%d",&b);que.push({b,i});}	que.pop();printf("%d",que.top().second);return 0;
}

C. Transportation Expenses

题目描述

有 \(N\) 个人，每个人有一个交通花费 \(A_i\)，你要炫富给他们进行交通补助 \(x\)，给每个人的钱为 \(min(x,A_i)\)，但是你的预算是 \(M\) 元，即 \(\sum\limits_{i=1}^{N}min(x,A_i)\le M\)，求最大的 \(x\)。如 \(x\) 可以无限大，输出infinite。\(1\le N\le2\times10^5\)，\(1\le M\le2\times10^{14}\)，\(1\le Ai\le10^9\)。

思路

首先有一个显然的结论：\(x=max_{i=1}^{N}A_i\) 时我们的花费最高。因为在这个值时所有人取到了 \(A_i\)，之后 \(x\) 变大无法影响我们的花费了。所以如果 \(\sum\limits_{i=1}^{N}A_i\ge M\)，我们就直接输出infinite好了。
然后再想对于其他情况，显然，随着 \(x\) 的增大，我们的花费是单调不减的，于是想到二分答案。对于一个确定的 \(x\)，直接暴力求值，然后和 \(M\) 比较即可。复杂度 \(O(n\log n)\)。注意 \(M\) 很大，要开long long。

代码

#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register long long
#define inf 0x3f3f3f3f
long long a,b,c[200002],sm,mx;
il bool check(long long x)
{ri rn=0;for(ri i=1;i<=a;i++){rn+=min(c[i],x);if(rn>b){return false;}}return true;
}
int main()
{scanf("%lld%lld",&a,&b);for(ri i=1;i<=a;i++){scanf("%lld",&c[i]);sm+=c[i];mx=max(mx,c[i]);}if(sm<=b){puts("infinite");exit(0);}ri l,m=0,n=mx;while(n-m>1){l=(m+n)>>1;if(check(l)){m=l;}else{n=l;}}if(check(n)){printf("%lld",n);}else{printf("%lld",m);}return 0;
}

D. AtCoder Janken 3

题目描述

两人玩石头剪刀布，规定A一定不败给B，且A相邻的操作一定不相同。现在给你B的操作序列 \(S\)，长为 \(N\)，求 \(A\) 最多胜利多少局。对于 \(S_i\)，R表示石头，P表示布，S表示剪刀。\(N\le2\times10^5\)

思路

一眼dp题。设 \(dp[i][0]\) 为第 \(i\) 出石头的最大获胜次数，\(dp[i][1]\) 为第 \(i\) 出布的最大获胜次数，\(dp[i][0]\) 为第 \(i\) 出剪刀的最大获胜次数。如果对方该局是石头，则我们必不能出剪刀，故不更新 \(dp[i][2]\)（初值是0）；如果我们出石头，继承上一局出剪刀和布的状态，但是该局不胜，直接转移；如果我们出布，继承上一局出剪刀和石头的状态，该局取胜，所以还要+1。对方出剪刀、布时同理。最后在第 \(N\) 次的三个答案中去最大值即可。复杂度 \(O(n)\)。

代码

#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register long long
#define inf 0x3f3f3f3f
int a,b[200002],dp[200002][5],ans;
char ch;
int main()
{scanf("%d",&a);for(ri i=1;i<=a;i++){ch=getchar();if(ch=='R'){b[i]=1;continue;}if(ch=='P'){b[i]=2;continue;}if(ch=='S'){b[i]=3;continue;}i--;}for(ri i=1;i<=a;i++){if(b[i]==1){dp[i][1]=max(dp[i-1][2],dp[i-1][3]);dp[i][2]=max(dp[i-1][1],dp[i-1][3])+1;continue;}if(b[i]==2){dp[i][2]=max(dp[i-1][1],dp[i-1][3]);dp[i][3]=max(dp[i-1][1],dp[i-1][2])+1;continue;}if(b[i]==3){dp[i][3]=max(dp[i-1][1],dp[i-1][2]);dp[i][1]=max(dp[i-1][2],dp[i-1][3])+1;continue;}}ans=max(dp[a][1],max(dp[a][2],dp[a][3]));printf("%d",ans);return 0;
}

E. Xor Sigma Problem

题目描述

给你一个长为 \(N\) 的序列 \(A\)，求\(\sum\limits_{i=1}^{N-1}\sum\limits_{j=i+1}^{N}A_i\oplus A_{i+1}\oplus\cdots\oplus A_j\)。\(1\le N\le2\times10^5\)，\(1\le A_i\le10^8\)

思路

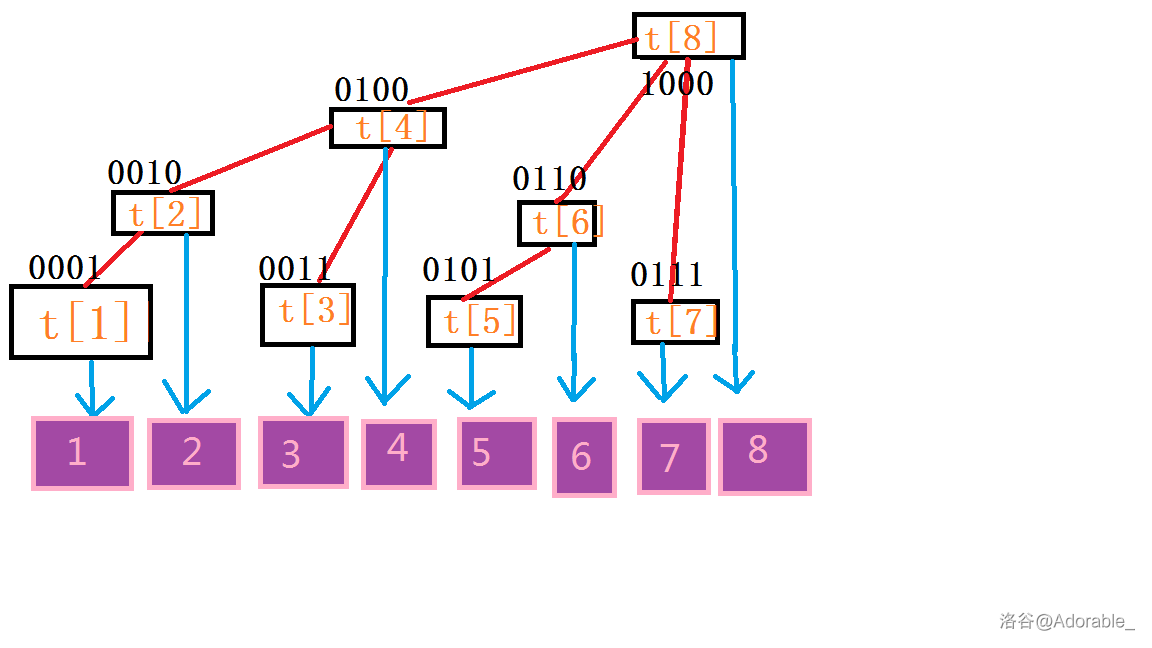
首先 \(O(N^2)\) 处理前缀和，然后 \(O(1)\) 求解相信大家都会，但是肯定会TLE。想要AC，至少要压掉一位，也就是对于每一个数实现 \(O(1)\) 求贡献。发扬人类智慧考虑异或运算的实质，我们尝试把一个整数拆成二进制串，针对每一个新加进来的数，找前面每一位出现的0/1的个数。注意，这里我们找的个数是针对每个后缀的，因为只有连续的区间可以产生贡献。但是如果把它们分开存，时间上又回到了 \(O(N^2)\)。于是，设 \(num[i][j][k]\) 为找到第 \(i\) 个数第 \(j\) 为出现的 \(k\) 的个数，\(dp[i]\) 为第 \(i\) 为产生的累计贡献，\(pre[i]\) 为异或前缀和，转移时注意细节处理，注意开大数组和long long。复杂度\(O(30N)\)。

代码

#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register long long
#define inf 0x3f3f3f3f
long long a,b[200002],pre[200002],num[200002][33][2],dp[33],ans;
int main()
{scanf("%lld",&a);for(ri i=0;i<=30;i++){num[0][i][0]=1;}scanf("%lld",&b[1]);pre[1]=b[1];for(ri j=0;j<=30;j++){ri k=(pre[1]>>j)&1;num[1][j][k]=num[0][j][k]+1;num[1][j][k^1]=num[0][j][k^1];}for(ri i=2;i<=a;i++){scanf("%lld",&b[i]);pre[i]=pre[i-1]^b[i];for(ri j=0;j<=30;j++){ri k=(pre[i]>>j)&1;dp[j]+=num[i-2][j][k^1];num[i][j][k]=num[i-1][j][k]+1;num[i][j][k^1]=num[i-1][j][k^1];}for(ri i=0;i<=30;i++){ans+=dp[i]*(1<<i);}printf("%lld",ans);return 0;
}