恒磁场 知识梳理

安培定律

\[\def\ooint{{\bigcirc}\kern-11.5pt{\int}\kern-6.5pt{\int}} \def\oooint{{\bigcirc}\kern-12.3pt{\int}\kern-7pt{\int}\kern-7pt{\int}} \]

  恒定电流只能存在于闭合回路中，但是闭合回路的形状是千变万化的，直接研究整个闭合回路的话问题会变得非常复杂。为此，干脆将载流回路分割为无限个无穷小的线元，叫做电流元，只要知道了任意一对电流元之间相互作用的基本规律，整个闭合回路的手里就可以通过矢量叠加计算出来。
在回路1中取一个电流元1，在回路2中取一个电流元2，设\({\rm d}\boldsymbol{F}_{12}\)为电流元给电流元2的力，\(I_1\)和\(I_2\)分别为它们的电流，\({\rm d}l_1\)和\({\rm d}l_2\)分别为两线元的长度，\(r_{12}\)为两电流元之间的距离，则

\[{\rm d}\boldsymbol{F}_{12}=k\frac{I_1I_2{\rm d}\boldsymbol{l}_2\times({\rm d}\boldsymbol{l}_1\times\boldsymbol{\hat{r}}_{12})}{{r_{12}}^2}\tag{2.12} \]

式中\(\boldsymbol{\hat{r}}_{12}\)为沿\(\boldsymbol{r}_{12}\)方向的单位矢量。上式就是安培定律的完整表达式。然而，由\((2.12)\)式确定的电流元之间的相互作用力不一定满足牛顿第三定律（牛顿第三定律只适用于质点间的接触作用）。但是实际中不存在孤立的恒定电流元，它们总是闭合回路的一部分。可以证明：若将\((2.12)\)式沿闭合回路积分，得到的合成作用力总是与反作用力大小相等、方向相反的。

电流单位——安培

  国际上现行的电磁学单位制是\(\rm{MKSA}\)制，\(\rm{A}\)即安培。“安培”这个基本单位的定义和绝对测量正是以\((2.12)\)为依据的。力的单位是\(\rm{N=kg\cdot m/s^2}\)长度的单位是\(\rm{m}\)，对于其余部分作以下操作：

1. 令比例系数\(k=\frac{\mu_0}{4\pi}\)；
2. 取\(\mu_0 = 4\pi\times10^{-7}\)；

这样确定下来的电流单位就是安培，记作\(\rm A\)。反过来可以定比例系数的量纲：

\[[\mu_0]=\frac{[F]}{[I]^2}=[F]I^{-2} \]

即

\[\mu_0=4\pi\times 10^{-7} \rm N/A^2 \]

磁感应强度 毕奥-萨伐尔定律

  库仑在得到点电荷之间的相互作用力的平方反比关系之后，经过实验证明了点磁荷之间也服从类似的公式

\[F=\frac{1}{4\pi\mu_0}\frac{q_{m1}q_{m2}}{r^2} \]

  上式称为磁的库仑定律。与电场强度的定义\(\boldsymbol{E}=\boldsymbol{F}/q_e\)对应地，我们引进磁场强度\(\boldsymbol{H}\)的概念

\[\boldsymbol{H}=\frac{\boldsymbol{F}}{q_{m0}} \]

  这里\(\boldsymbol{F}\)是试探点磁荷\(q_{m0}\)所受的力。由此可见，磁场强度矢量\(\boldsymbol{H}\)是从磁荷间的相互作用出发定义的物理量。现在我们从电流间的相互作用出发也可以定义一个描述磁场的矢量——磁感应强度矢量\(\boldsymbol{B}\).在\(\rm{MKSA}\)单位制下，真空中二者的关系为

\[\boldsymbol{B}=\mu_0\boldsymbol{H} \]

  为了求出磁感应强度的表达式，不妨采用类似于试探电荷的思路。先在\(\rm{MKSA}\)单位制中将安培定律\((2.12)\)改写为

\[{\rm d}\boldsymbol{F}_{12}=\frac{\mu_0}{4\pi}\frac{I_1I_2{\rm d}\boldsymbol{l}_2\times({\rm d}\boldsymbol{l}_1\times\boldsymbol{\hat{r}}_{12})}{{r_{12}}^2}\tag{2.17} \]

  然后，将电流元\(I_2{\rm d}\boldsymbol{l}_2\)视作试探电流元，将\({\rm d}\boldsymbol{F}_{12}\)视作电流元2所受的力\({\rm d}\boldsymbol{F}_2\)，用这个力来描述磁感应强度。上式拆分成两部分：

\[{\rm d}\boldsymbol{F}_{2}=I_2{\rm d}\boldsymbol{l}_2\times{\rm d}\boldsymbol{B}\tag{2.18}\]

\[\boldsymbol{B}= \oint_{L1} {\rm d}\boldsymbol{B}= \frac{\mu_0}{4\pi}\oint_{L1}\frac{I_1{\rm d}\boldsymbol{l}_1 \times\boldsymbol{\hat{r}}_{12}}{{r_{12}}^2}\tag{2.19} \]

  \((2.18)\)式是磁感应强度的定义式，\((2.19)\)是闭合回路\(L_1\)在电流元2的位置产生的磁感应强度的公式。有趣的是，\((2.18)\)式实际上拓展了\({\rm d}\boldsymbol{F}_2\)的含义，此时的磁场\(\boldsymbol{B}\)可以是某个闭合回路产生的，也可以是磁铁等场源产生的。
关于磁感应强度的单位：按照\((2.18)\)定义，\(\boldsymbol{B}\)的单位是\(\rm N/A\cdot m\)，这其实就是特斯拉，用\(\rm T\)表示。另外，实际中另一种单位也很常见——高斯，用\(\rm Gs\)表示。例如，线性霍尔AH49E的数据手册用的就是Gs:

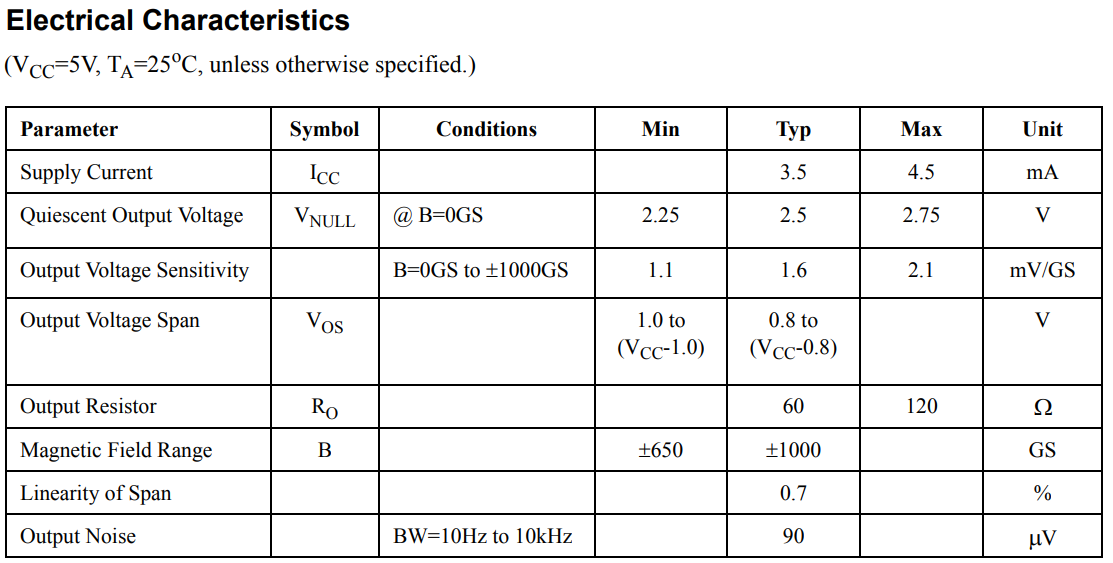
两个单位的换算关系是

\[1{\rm T} = 10^4 \rm Gs \]

毕奥-萨伐尔定律

为了计算各种回路产生的磁场分布，由\((2.19)\)，取任意闭合回路、任意场点，略去1、2不写，有

\[\boldsymbol{B}=\frac{\mu_0}{4\pi}\oint_{L}\frac{I{\rm d}\boldsymbol{l} \times\boldsymbol{\hat{r}}}{{r}^2}\tag{2.19} \]

这就是毕奥-萨伐尔定律。

亥姆霍兹线圈

  取一对相同的圆形线圈，彼此平行且共轴。设两线圈内的电流都是\(I\)，且回绕方向一致，线圈的半径为\(R\)，二者的间距为\(a\)，\((1)\)求轴线上的磁场分布；\((2)\)\(a\)多大时据两线圈等远的中点\(O\)附近的磁场最均匀？

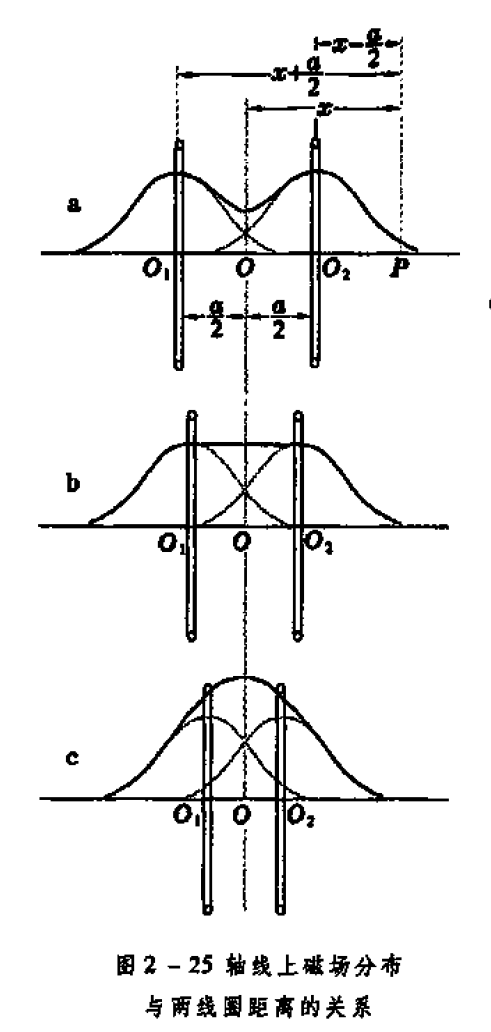
建立如图坐标系。如果两个线圈间距太远，则原点处有极小值；如果两个线圈间距太近，则原点处出现极大值。只要距离\(a\)取得合适，可以使得\(x=0\)处\({\rm d}^2B/{\rm d}x^2=0\),这时在\(O\)点附近的磁场应当是相当均匀的。即，对于不同的\(a\)来说，\(O\)点附近磁场最均匀的条件是

\[在x=0处\quad \frac{{\rm d}^2 B}{{\rm d}x^2}=0 \]

这一条件也可以用泰勒级数更严谨地证明。令\(B(x)\)代表总的磁感应强度，在 \(x=0\) 处的泰勒展开为

\[B(x)=B(0)+x\left(\frac{{\rm d}B}{{\rm d}x}\right)_{x=0}+\frac{x^2}{2!}\left(\frac{{\rm d}^2 B}{{\rm d}x^2}\right)_{x=0}+\frac{x^3}{3!}\left(\frac{{\rm d}^3 B}{{\rm d}x^3}\right)_{x=0}+\cdots \]

由于\(B(x)=B(-x)\)，即\(B(x)\)是关于\(x\)的偶函数，所以奇次项都等于0.进一步地，如果\(\left(\frac{{\rm d}^2 B}{{\rm d}x^2}\right)_{x=0}=0\)，则

\[B(x)=B(0) + \frac{x^4}{4!}\left(\frac{{\rm d}^4 B}{{\rm d}x^4}\right)_{x=0}+o(x^4) \]

新概念物理中直接将第二项和第三项合并称为\(O(x^4)\)，认为它代表的是\(x\)的四次方及更高幂次的小量，但是我没记错的话它只能代表更高阶的小量，莫非\(o\)的大小写还会带来不同的含义🤔不管怎么说，结论就是\(B(x)\)将在相当大的范围内均匀。
后面的推导无非就是将磁感应强度的表达式写出来，再求导，令二阶导函数等于零，过程就不打了。结论是，O点附近场强最均匀的条件为

\[a=R \]

即两线圈的间距等于他们的半径。这种间距等于半径的一对共轴圆线圈，称为亥姆霍兹线圈。这种线圈可以产生均匀磁场，当所需的磁场强度不太大时，用它比较方便。

螺线管

  设无限长螺线管的单位长度的匝数为\(n\)，每匝的电流为\(I\)，则无限长螺线管产生的磁场为

\[B=\mu_0 n I \]

安培环路定理

载流线圈与磁偶极层的等价性

闭合载流线圈产生的磁场正比于线圈回路对场点所张立体角的梯度：

\[\boldsymbol{B} = \frac{\mu_0 I}{4\pi}\boldsymbol\nabla\Omega \]

这一结论是由毕奥-萨伐尔定律推出，可以用于证明安培环路定理，此处从略。

安培环路定理

表述:磁感应强度沿任何闭合环路\(L\)的线积分，等于穿过这环路所有电流的代数和的\(\mu_0\)倍。用公式来表示，则有

\[\oint_L \boldsymbol{B}{\rm d}\boldsymbol{l} = \mu_0\sum I_{encl} \]

其中电流\(I\)的正负规定为：当穿过回路的电流方向与回路的环绕方向服从右手定则时，\(I>0\)，反之，\(I<0\)。如果电流不穿过回路，则它对上式右端无贡献。但是\(\boldsymbol{B}\)包含了空间中所有电流产生的磁场强度的矢量和，包括那些不穿过回路的电流，只不过这些电流最后沿闭合回路积分后的总效果等于0。

关于对称性

一个系统在任何操作下下的不变性，都是“对称性”。绕固定轴旋转的不变性是轴对称性，绕固定点旋转的不变性是球对称性，沿特定方向平移的不变性是平移对称性，等等。在对称的条件下必然有对称的结果，例如点电荷具有球对称性，故电场的分布必然是球对称的，这便是对称性原理。在电磁学中对称性原理的应用特别突出。

在空间反射下的不变性叫做镜像对称性。建立一个空间直角坐标系\(Oxyz\)，它在镜面后成的像为左手坐标系\(O'x'y'z'\)。其中，\(x\)轴、\(y\)轴分别和\(x'\)轴和\(y'\)轴同向平行，\(z\)轴和\(z'\)轴反向平行，这就是镜像反射变换。

根据镜像反射变换的结果不同，可以将矢量分为极矢量和轴矢量。如果矢量变换后与镜面垂直的分量反向，平行分量不变，则这类矢量称为极矢量。如果矢量变换后与镜面垂直的分量不变，平行的分量反向，则这类矢量称为轴矢量。例如，磁感应强度\(\boldsymbol{B}\)、磁矩\(\boldsymbol{m}\)都是轴矢量。容易证明，两个极矢量相乘，得到的是轴矢量。

按照毕奥-萨伐尔定律，磁感应强度是电流元和矢径的叉乘\(({\rm d}\boldsymbol{l} \times \boldsymbol{r})\)，因此磁感应强度是轴矢量。由此可以得到一个重要的推论：镜面对称的载流系统产生的磁感应强度必与该面垂直，也就是没有水平分量，只有垂直分量。

磁场的高斯定理 磁矢势

磁场的“高斯定理”

规定通过一个闭合曲面\(S\)的磁通量为

\[\Phi_b=\ooint_S \boldsymbol{B \cdot}{\rm d}\boldsymbol S \]

由于磁感线总是闭合的，从一个曲面穿进，必定会从某一处穿出，因此通过闭合曲面的磁通量为0

\[\Phi_b=\ooint_S \boldsymbol{B \cdot}{\rm d}\boldsymbol S = 0 \]

这就是磁场的“高斯定理”。

磁矢势

参考:磁矢势-小时百科
磁场中的磁矢势与静电场中的电势在概念上相当，只不过前者是矢量，后者是标量。
引入
磁感应强度\(\boldsymbol{B}\)永远是一个无散场。根据旋度的逆运算定理1，任何无散场\(\boldsymbol{B}\)可以表示成某个矢量场\(\boldsymbol{A}\)的旋度，即

\[\boldsymbol{B} = \boldsymbol{\nabla\times}\boldsymbol{A} \]

这个\(\boldsymbol{A}\)就是磁矢势。

磁场对载流导线的作用

安培力

将式(2.18)略去下标，得

\[{\rm d}\boldsymbol{F}=I{\rm d}\boldsymbol{l\times}\boldsymbol{B} \]

这就是安培力。

磁矩

对于处于均匀磁场中的任意形状的载流平面线圈，设它的右旋法向矢量为\(\boldsymbol{n}\)，磁矩为

\[\boldsymbol{m}=IS\boldsymbol{n} \]

受到的力矩为

\[\boldsymbol{L}=\boldsymbol{m\times B} \]

任意形状的载流平面线圈作为整体，在均匀外磁场中不受力，但受到一个力矩，这力矩总是试图使线圈的磁矩\(\boldsymbol{m}\)转到磁感应强度\(\boldsymbol{B}\)的方向。

带电粒子在磁场中受力

洛伦兹力

\[\boldsymbol{F}=q\boldsymbol{v\times}\boldsymbol{B} \]

霍尔效应

把一片载流导体薄片放置于磁场中时，如果磁场方向垂直于薄片平面，则在薄片的上、下两侧面会出现微弱的电势差。这一现象称为霍尔效应（Hall effect）。此电势差称为霍尔电势差。实验测定，霍尔电势差的大小与电流\(I\)和磁感应强度\(B\)成正比，与导体沿\(B\)方向的厚度成反比。它们的关系可写成

\[V=R_H\frac{IB}{d} \]

\(R_H\)是霍尔系数（Hall coefficient）

\[R_H=\frac{1}{nq} \]

半导体内载流子的浓度远比金属中的载流子浓度小，所以半导体的霍尔效应要显著得多。