Tarjan 之 SCC 与 缩点

这篇文章将讲述作者对 Tarjan求SCC与缩点（不是割点）的理解

让我们开始吧！

Tarjan SCC 与 缩点

既然要求 \(SCC\) 那我们先要弄明白 什么是 SCC

SCC 指的是强连通分量

强连通指的是若一张有向图的节点两两互相可达，则这张图是强连通的

而强连通分量 指的是一个极大的连通子图
此处的极大指的是一个子图再多一个节点都将不强连通

那么知道了这个，我们就可以继续了

tarjan求SCC的算法和之前求 LCA 的Tarjan 有些类似之处

这是tarjan求SCC所需的数组

• \(dfn[x]\) 表示 \(x\) 节点的DFN序即遍历顺序
• \(low[x]\) 表示 \(x\) 节点所能到达的 DFN序最小 的节点 PS：可以经过多条边
• \(stk[]\) 求SCC所需的栈
• \(instk[x]\) 表示 \(x\) 节点是否在栈中
• \(scc[x]\) 表示 \(x\) 节点在编号为几的 SCC之中
• \(siz[k]\) 表示 编号为 \(k\) 的一个SCC的大小

其中 \(dfn\) , \(low\) , \(instk\) 和 \(scc\) 都是可以放在一个结构体中的

数组有点多，不要慌， 我们一点点来讲讲算法的流程

首先，对于一个图，我们在深搜遍历时，每个点只会进入一次，而这将产生一个搜索树

例如对这个图

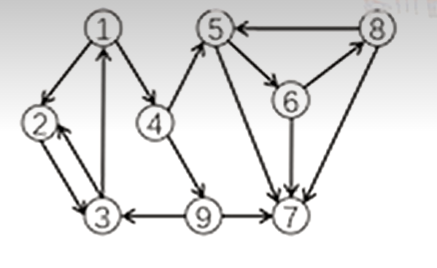
我们会产生一颗如下的搜索树

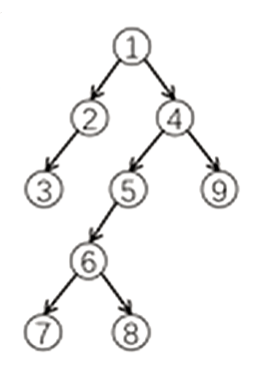
当我们在深搜进入点 \(x\) 时， 标记其 的深搜序 然后把它放入栈中

然后遍历他的所有边能到的点 \(y\)

y 有且仅有 3 种情况

1. y没被遍历过且不在栈中 对于这种情况，我们继续递归 \(y\) 然后 用 \(low[y]\) 来更新 \(low[x]\) 就是将 \(low[x]\) 变成 \(low[x]\)与\(low[y]\) 最小的那个

2. y被遍历过且在栈中，对于这种情况我们用 \(low[y]\) 来更新 \(low[x]\)

3. y被遍历过且在栈中，说明这个点我们已经处理完了,就不用管了

在遍历完后，我们检查 \(dfn[x]\) 是否等于 \(low[x]\)
若相等，则说明 \(x\) 是一个 SCC 的根

先证明为什么，然后再继续讲

由 \(low[x]\) 的定义可得，\(x\) 所能到达的 \(dfn\) 编号最小的节点就是 他自己

就像这个图

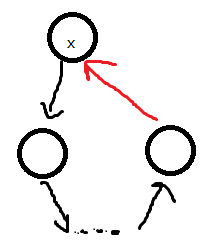
由于 \(x\) 能够走到他自己，那么 \(x\) 一定在一个环中，再感性理解一下（我还不知道怎么证明这是极大的 QwQ upt：证明见下面），\(x\) 一定是一个 SCC 的根

所以，我们不断弹栈知道将 \(x\) 弹出去，将弹出去的每个节点标记所在的 SCC 编号，然后取消入栈标记, 将 \(siz[编号]++\)

这是因为以 \(x\) 为根的 SCC 一定都在 \(x\) 之后入栈 ，而所有的不在 以 \(x\) 为根的 SCC 中 的 节点 一定 在回溯到 \(x\) 之前已经被相同的流程处理掉了，已经出栈了，栈中还在 \(x\) 之后的一定都属于以 \(x\) 为根的 SCC

以一个图为例子

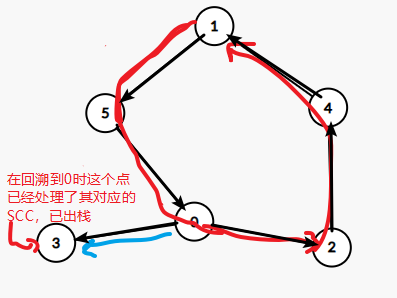
还有没讲详细的后面再补吧，结合代码感性理解一下

上代码

#include<bits/stdc++.h>
using namespace std;
int n,m;
struct node
{vector<int> to;//能到达的点int dfn;int low;//能访问到的dfn最小的节点bool instk;bool vis;
};
node nodes[1000000];
int tot;//dfn
int stk[100000],scc[100000],siz[100000]/*SCC大小*/,cnt/*SCC编号*/,top/*栈顶*/;void tarjan(int x)
{nodes[x].dfn=++tot;//记录DFNnodes[x].low=tot;stk[++top]=x;nodes[x].instk=1;int to_;for(int y=0; y<nodes[x].to.size(); y++){to_=nodes[x].to[y];if(nodes[to_].dfn==0)//若没访问过 {tarjan(to_);//深搜nodes[x].low=min(nodes[x].low,nodes[to_].low);//更新}else if(nodes[to_].instk)//若y已访问且在栈中 {nodes[x].low=min(nodes[x].low,nodes[to_].dfn);//更新}}if(nodes[x].dfn==nodes[x].low)//若这个节点能链接到自己说明是一个SCC的根 {int y;cnt++;do//将节点出栈{y=stk[top--];nodes[y].instk=0;scc[y]=cnt;++siz[cnt];}while(y!=x);}}
int main()
{ios::sync_with_stdio(0);cin>>n>>m;int a,b;for(int ww=1;ww<=m;ww++){cin>>a>>b;nodes[a].to.push_back(b);}for(int i=1;i<=n;i++){if(!nodes[i].dfn)//图可能不联通{tarjan(i);}}cout<<cnt;return 0;}

---

啊对了，还有缩点

简单来说就是把一个 SCC 看做一个点来处理，啊应该就是这样，没了

---

完结·散花！

没想到这样一篇文章要写整整一个小时啊啊啊