动态dp

T1

一共 \(n\) 颗糖果,第 \(i\) 颗的价值为 \(a[i]\),你不能连着选两颗,请问你的选到的最大价值为多少
显然有如下写法 :
设 \(dp[i][0/1]\)表示选到了第 \(i\) 颗,第 \(i\) 颗选或不选
显然有转移 :
\(dp[i][0] = max(dp[i - 1][0], dp[i - 1][1])\)
\(dp[i][1] = max(dp[i - 1][0] + a[i], dp[i][1] - INF)\)
那么可以列出一下矩阵 :
\([0, 0]\)
\([a[i], -INF]\)
在考虑 \(i + 1\) 的转移 :
\(dp[i + 1][0] = max(dp[i][0], dp[i][1])\)
\(dp[i + 1][1] = max(dp[i][0] + a[i + 1], dp[i][1] - INF)\)
将两个转移结合可得 :
\(dp[i + 1][0] = max(dp[i - 1][0], dp[i - 1][0], dp[i - 1][0] + a[i], dp[i][1] - INF)\)
\(dp[i + 1][1] = max(dp[i - 1][0] + a[i + 1], dp[i - 1][1] + a[i + 1], dp[i - 1][0] + a[i] - INF, dp[i][1] - INF - INF)\)
简化得 :
如果将
\([a, b]\)
\([c, d]\)
与
\([e, f]\)
\([g, h]\)
合并,可得出下矩阵
\([max(a + e, b + g), max(a + f, b + h)]\)
\([max(c + e, d + g), max(c + f, d + h)]\)
我们来考虑如果需要修改如何计算, 即:
给定 \(q\) 个查询,每次将 \(a[p]\) 改为 \(x\),请输出你选到的最大价值
我们只需要将这些 \(2 \times 2\) 的矩阵缩进一个线段树里,线段树的合并操作按照前面矩阵的合并操作合并即可,下面为合并操作的代码

for (int a : {0, 1}) {for (int b : {0, 1}) {for (int c : {0, 1}) {tr[i][a][b] = max(tr[i][a][b], tr[i * 2][a][c] + tr[i * 2 + 1][c][b]);}}
}

Count Paths Queries

我们可以记录 \(g[i][j][k]\) 表示从 \(i\) 至 \(j\), 最多走了 \(2 ^ k\) 步的最大价值
那么显然这个数组有单调性,倍增考虑即可

#include <bits/stdc++.h>using namespace std;const int N = 2e2 + 5, mod = 1e9 + 7;int n, m, q, g[31][N][N], dp[N], tmp[N];int main() {ios::sync_with_stdio(0);cin.tie(0);cin >> n >> m >> q;for (int i = 1, u, v; i <= m; i++) {cin >> u >> v;g[0][u][v] = 1;}for (int i = 1; i <= 30; i++) {for (int a = 1; a <= n; a++) {for (int b = 1; b <= n; b++) {for (int c = 1; c <= n; c++) {g[i][a][b] = (g[i][a][b] + 1ll * g[i - 1][a][c] * g[i - 1][c][b]) % mod;}}}}while (q--) {int s, t, k;cin >> s >> t >> k;fill(dp + 1, dp + n + 1, 0);dp[s] = 1;for (int i = 30; i >= 0; i--) {if (k >= (1 << i)) {k -= (1 << i);for (int j = 1; j <= n; j++) {tmp[j] = dp[j];dp[j] = 0;}for (int j = 1; j <= n; j++) {for (int k = 1; k <= n; k++) {dp[k] = (dp[k] + 1ll * tmp[j] * g[i][j][k]) % mod;}}}}cout << dp[t] << "\n";}return 0;
}

洛谷P4719

我们显然可以列出一个树形 \(dp\) :

void dfs(int u, int f) {dp[u][1] = a[u];fa[u] = f;for (auto v : g[u]) {if (v == f) {continue;}dfs(v, u);dp[u][0] += max(dp[v][1], dp[v][0]);dp[u][1] += dp[v][0];}
}

但是,如果每次查询都从 \(x\) 开始,跑到根节点,那么时间复杂度来到了 \(O(n \times m)\)而序列 \(dp\) 又不能在树上进行,咋办呢?只需要将树剖成一条一条链,然后在链与链的交点处特别处理一下 \(dp\) 即可,如图 :

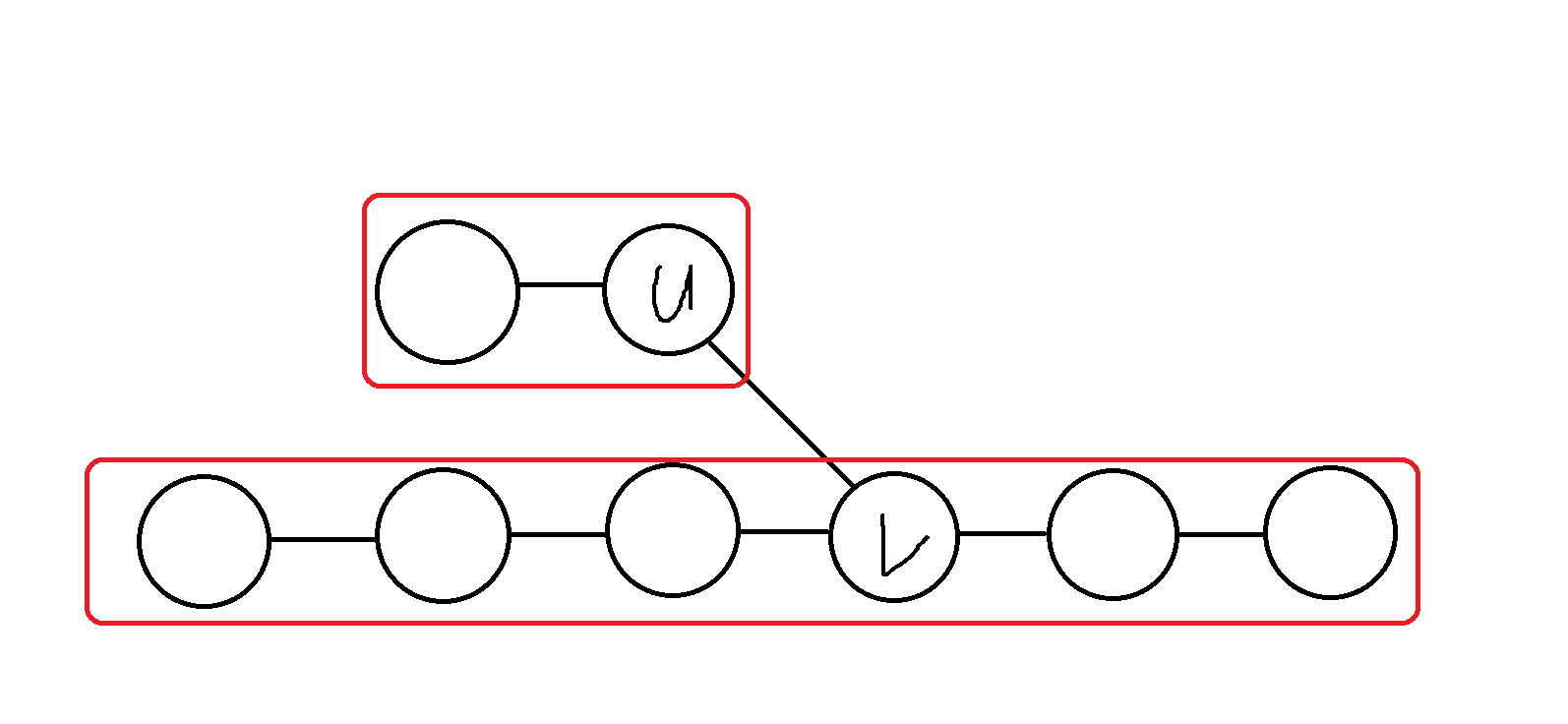
那么 \(dp[u][0] += max(dp[v][1], dp[v][0])\), \(dp[u][1] += dp[v][0]\)
剩下的就是本片博客的 T1 部分

#include <bits/stdc++.h>using namespace std;#define int long longconst int N = 1e5 + 5, INF = 2e18;int n, m, a[N], dp[N][2];int dcnt, dfn[N], sz[N], top[N], fa[N], son[N], tail[N];struct node {int a[2][2];
}tr[N * 4];vector<int> g[N];node Merge(const node &l, const node &r) {node tmp = {-INF, -INF, -INF, -INF};for (int i : {0, 1}) {for (int j : {0, 1}) {for (int k : {0, 1}) {tmp.a[i][j] = max(tmp.a[i][j], l.a[i][k] + r.a[k][j]);}}}return tmp;
}node query(int i, int l, int r, int x, int y) {if (l >= x && r <= y) {return tr[i];}int mid = (l + r) >> 1;if (x <= mid && y > mid) {return Merge(query(i * 2, l, mid, x, y), query(i * 2 + 1, mid + 1, r, x, y));}if (x <= mid) {return query(i * 2, l, mid, x, y);}if (y > mid) {return query(i * 2 + 1, mid + 1, r, x, y);}return {-INF, -INF, -INF, -INF};
}void modify(int i, int l, int r, int p, const node &cur) {if (l == r) {tr[i] = cur;return ;}int mid = (l + r) >> 1;if (mid >= p) modify(i * 2, l, mid, p, cur);else modify(i * 2 + 1, mid + 1, r, p, cur);tr[i] = Merge(tr[i * 2], tr[i * 2 + 1]);
}void dfs1(int u, int f) {fa[u] = f;sz[u] = 1;for (auto v : g[u]) {if (v == f) {continue;}dfs1(v, u);sz[u] += sz[v];if (sz[son[u]] < sz[v]) {son[u] = v;}}
}void dfs2(int u, int f) {dfn[u] = ++dcnt;if (son[u]) {top[son[u]] = top[u];dfs2(son[u], u);}else tail[top[u]] = u;for (auto v : g[u]) {if (v == son[u] || v == f) {continue;}top[v] = v;dfs2(v, u);auto cur = query(1, 1, n, dfn[v], dfn[tail[v]]);dp[u][1] += cur.a[0][0];dp[u][0] += max(cur.a[1][0], cur.a[0][0]);}modify(1, 1, n, dfn[u], {dp[u][0], dp[u][0], dp[u][1] + a[u], -INF});
}signed main() {cin >> n >> m;for (int i = 1; i <= n; i++) {cin >> a[i];}for (int i = 1, u, v; i < n; i++) {cin >> u >> v;g[u].push_back(v);g[v].push_back(u);}dfs1(1, 0);top[1] = 1;dfs2(1, 0);while (m--) {int p, x;cin >> p >> x;a[p] = x;while (p) {//对 p 至他的链头做修改int tp = top[p];auto cur = query(1, 1, n, dfn[tp], dfn[tail[tp]]);dp[fa[tp]][1] -= cur.a[0][0];dp[fa[tp]][0] -= max(cur.a[0][0], cur.a[1][0]);modify(1, 1, n, dfn[p], {dp[p][0], dp[p][0], dp[p][1] + a[p], -INF});cur = query(1, 1, n, dfn[tp], dfn[tail[tp]]);dp[fa[tp]][1] += cur.a[0][0];dp[fa[tp]][0] += max(cur.a[0][0], cur.a[1][0]);p = fa[tp];}auto cur = query(1, 1, n, dfn[1], dfn[tail[1]]);cout << max(cur.a[0][0], cur.a[1][0]) << "\n";}return 0;
}
/*