题目描述
P1149
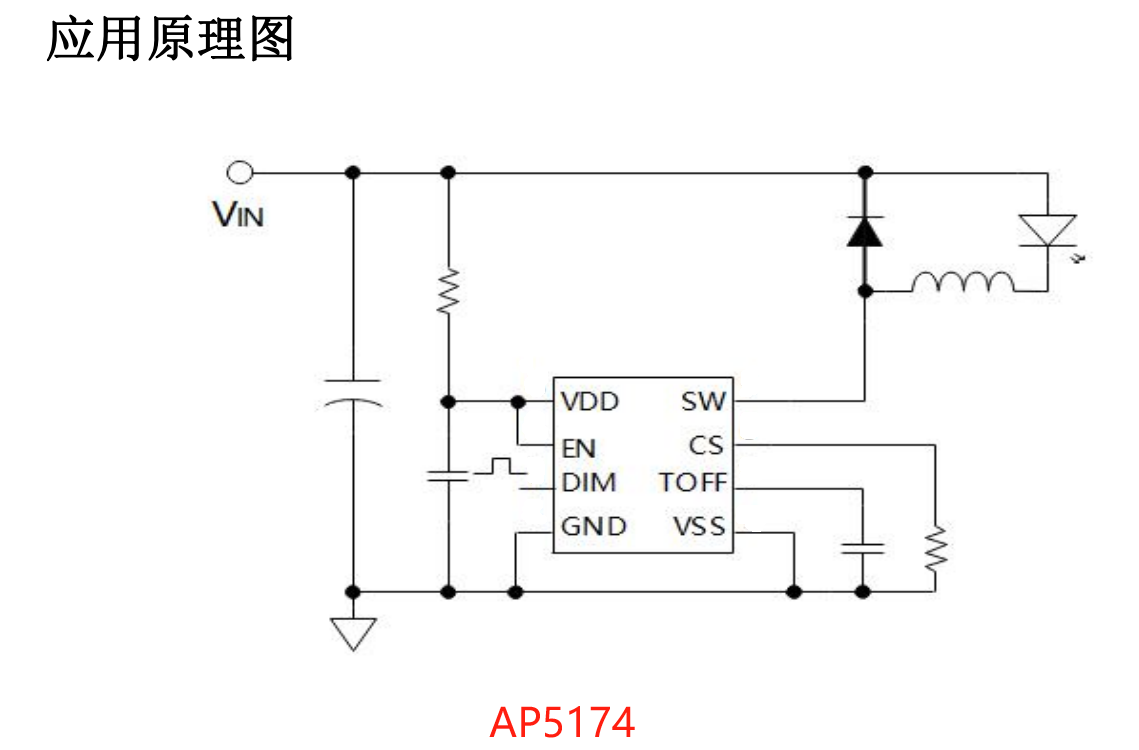
给你 \(n\) 根火柴棍,你可以拼出多少个形如 \(A+B=C\) 的等式?等式中的 \(A\)、\(B\)、\(C\) 是用火柴棍拼出的整数(若该数非零,则最高位不能是 \(0\))。用火柴棍拼数字 \(0\sim9\) 的拼法如图所示:
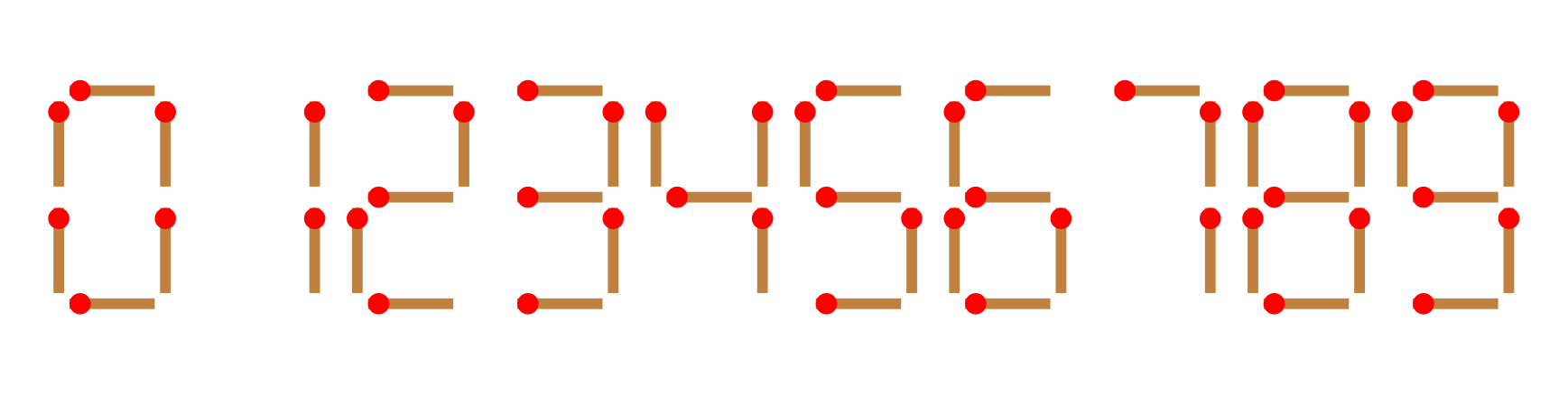
注意:
- 加号与等号各自需要两根火柴棍;
- 如果 \(A\neq B\),则 \(A+B=C\) 与 \(B+A=C\) 视为不同的等式(\(A,B,C\geq0\));
- \(n\) 根火柴棍必须全部用上。
原题中 \(n \leq 24\),我们希望能做到更大。
当然,方案数(也许)会相当多,为了不写高精,我们可以将答案对某个质数取模(比如 \(10^9+7\))。
定个小目标,看看能不能做到 \(n \leq 100\) 。
由于 \(n\) 的范围增大,枚举一个数的代价相当高,原题中基于可能的 \(A,B,C\) 很小的做法不再适用,我们需要另辟蹊径。
尝试搜索,首先去除加号与等于号(将 \(n\) 减四),然后自低位向高位考虑 \(A,B\) 每一位的取值并计算是否合法。
想想我们需要知道什么:当前搜索到的深度(即从低到高的位数),上一位是否有进位,当前用了多少火柴棍。
容易写出简单的代码。
int cnt[]={6,2,5,5,4,5,6,3,7,6};
void dfs(int k,int carry,int sum){//k :当前考虑的位置,carry :上一位的进位,sum :还未用的火柴棍数量//calc the answerfor(int a=0;a<=9;a++)for(int b=0;b<=9;b++){//枚举A,B的第 k 位所填的数int tmp=a+b+carry;int c=tmp/10,new_carry=tmp/10;dfs(k+1,new_carry,sum-cnt[a]-cnt[b]-cnt[c]);}
}
但这个代码会有些问题:当 \(A\) 或 \(B\) 中的某个数已经填完后,我们的算法会往前补前导 \(0\),这是题目所不允许的;同时,答案的统计也不方便。
由此,我们可以在填到某个位置后钦定 \(A\) 或 \(B\) 被 “截断”, 即强制 \(A\) 或 \(B\) 中的某个数以后只能选 \(0\),且不计入火柴棍总数,由此来尝试规避前导 \(0\) 对答案的影响。
每次填数后,考虑 \(A,B\) 是否被截断。仅需额外开两维记录。
这样一来,统计答案变得十分方便:当 \(A\) 和 \(B\) 都被截断时进行统计,若此时无进位,则 \(sum = 0\) 时加入答案;若此时有进位,则 \(sum = 2\) 时加入答案。
int ans;
int cnt[]={6,2,5,5,4,5,6,3,7,6};
void dfs(int k,int carry,bool cuta,bool cutb,int sum){//cuta,cutb:a,b是否被截断if(cuta&&cutb){if((!carry&&sum==0)||(carry&&sum==2))ans++;return;}for(int a=0;a<=9;a++){if(cuta&&a!=0)break;for(int b=0;b<=9;b++){if(cutb&&b!=0)break;int tmp=a+b+carry;int c=tmp/10,new_carry=tmp/10;int new_sum=sum;if(!cuta)new_sum-=cnt[a];if(!cutb)new_sum-=cnt[b];new_sum-=cnt[c];if(new_sum<0)continue;if(!cuta&&!cutb){//枚举A,B是否截断dfs(k+1,new_carry,0,0,new_sum);dfs(k+1,new_carry,0,1,new_sum);dfs(k+1,new_carry,1,0,new_sum);dfs(k+1,new_carry,1,1,new_sum);}else if(!cuta&&cutb){dfs(k+1,new_carry,0,1,new_sum);dfs(k+1,new_carry,1,1,new_sum);}else if(cuta&&!cutb){dfs(k+1,new_carry,1,0,new_sum);dfs(k+1,new_carry,1,1,new_sum);}else dfs(k+1,new_carry,1,1,new_sum);}}
}
但是在原题会 WA 一个点。

而且效率相当低,\(n=50\) 左右就稳定的跑不过去。
还是因为前导 \(0\) 的影响,\(A\) 或 \(B\)可以先选上一串前导 \(0\),然后再悠哉游哉地截断,我们的截断毫无作用。
可以注意到,如果当前位被填了 \(0\),那么当前位一定不能被截断(除非这个数就是 \(0\)),于是可以在截断时特判,只有在当前位非 \(0\) 或当前是第一位才允许截断。
int ans;
int cnt[]={6,2,5,5,4,5,6,3,7,6};
void dfs(int k,int carry,bool cuta,bool cutb,int sum){if(cuta&&cutb){if((!carry&&sum==0)||(carry&&sum==2))ans++;return;}for(int a=0;a<=9;a++){if(cuta&&a!=0)break;for(int b=0;b<=9;b++){if(cutb&&b!=0)break;int tmp=a+b+carry;int c=tmp%10,new_carry=tmp/10;int new_sum=sum;if(!cuta)new_sum-=cnt[a];if(!cutb)new_sum-=cnt[b];new_sum-=cnt[c];if(new_sum<0)continue;bool allowcuta=a!=0||k==1,allowcutb=b!=0||k==1;//只有当前位非0或在第一位才允许截断if(!cuta&&!cutb){dfs(k+1,new_carry,0,0,new_sum);if(allowcuta)dfs(k+1,new_carry,0,1,new_sum);if(allowcutb)dfs(k+1,new_carry,1,0,new_sum);if(allowcuta&&allowcutb)dfs(k+1,new_carry,1,1,new_sum);}else if(!cuta&&cutb){dfs(k+1,new_carry,0,1,new_sum);if(allowcuta)dfs(k+1,new_carry,1,1,new_sum);}else if(cuta&&!cutb){dfs(k+1,new_carry,1,0,new_sum);if(allowcutb)dfs(k+1,new_carry,1,1,new_sum);}else dfs(k+1,new_carry,1,1,new_sum);}}
}
现在可以通过原题了,但跑 \(n=50\) 还是要两三秒。
可以发现,目前我们的搜索向下递归的参数有且仅有函数的参数,没有任何额外信息(比如回溯需要的信息)。因此,可以使用记忆化搜索存储每个状态。
int cnt[]={6,2,5,5,4,5,6,3,7,6};
int f[N][2][2][2][N];//不难发现,每次进位最多为 1,所以 carry 这维仅需开到 2
int dfs(int k,int carry,bool cuta,bool cutb,int sum){if(cuta&&cutb){if((!carry&&sum==0)||(carry&&sum==2))return 1;else return 0;}if(f[k][carry][cuta][cutb][sum]!=-1)return f[k][carry][cuta][cutb][sum];int ret=0;for(int a=0;a<=9;a++){if(cuta&&a!=0)break;for(int b=0;b<=9;b++){if(cutb&&b!=0)break;int tmp=a+b+carry;int c=tmp%10,new_carry=tmp/10;int new_sum=sum;if(!cuta)new_sum-=cnt[a];if(!cutb)new_sum-=cnt[b];new_sum-=cnt[c];if(new_sum<0)continue;bool allowcuta=a!=0||k==1,allowcutb=b!=0||k==1;if(!cuta&&!cutb){(ret+=dfs(k+1,new_carry,0,0,new_sum))%=mod;if(allowcuta)(ret+=dfs(k+1,new_carry,0,1,new_sum))%=mod;if(allowcutb)(ret+=dfs(k+1,new_carry,1,0,new_sum))%=mod;if(allowcuta&&allowcutb)(ret+=dfs(k+1,new_carry,1,1,new_sum))%=mod;}else if(!cuta&&cutb){(ret+=dfs(k+1,new_carry,0,1,new_sum))%=mod;if(allowcuta)(ret+=dfs(k+1,new_carry,1,1,new_sum))%=mod;}else if(cuta&&!cutb){(ret+=dfs(k+1,new_carry,1,0,new_sum))%=mod;if(allowcutb)(ret+=dfs(k+1,new_carry,1,1,new_sum))%=mod;}else (ret+=dfs(k+1,new_carry,1,1,new_sum))%=mod;}}return f[k][carry][cuta][cutb][sum]=ret;
}
程序效率得到了质的飞跃,\(n = 100\) 很快就跑过去了,\(n=1000\) 一秒内也冲过去了。
还能更进一步吗?比如 \(n=30000\) ?
乍一看有点难:总的状态数已经是 \(\Theta(n^2)\) 的了,怎么进一步优化?
仔细看:\(k\) 这一维似乎相当没用。\(k\) 唯一的用处就是判断前导 \(0\),没有任何其他用途。
事实上,我们仅需知道 \(k\) 是否等于 \(1\) 以判断前导 \(0\),因此可以直接将第一维压至 \(0/1\)。
int cnt[]={6,2,5,5,4,5,6,3,7,6};
int f[2][2][2][2][N];
int dfs(bool k,bool carry,bool cuta,bool cutb,int sum){if(cuta&&cutb){if((!carry&&sum==0)||(carry&&sum==2))return 1;else return 0;}if(f[k][carry][cuta][cutb][sum]!=-1)return f[k][carry][cuta][cutb][sum];int ret=0;for(int a=0;a<=9;a++){if(cuta&&a!=0)break; for(int b=0;b<=9;b++){if(cutb&&b!=0)break;int tmp=a+b+carry;int c=tmp%10,new_carry=tmp/10;int new_sum=sum;if(!cuta)new_sum-=cnt[a];if(!cutb)new_sum-=cnt[b];new_sum-=cnt[c];if(new_sum<0)continue;bool allowcuta=a!=0||k==1,allowcutb=b!=0||k==1;if(!cuta&&!cutb){(ret+=dfs(0,new_carry,0,0,new_sum))%=mod;if(allowcuta)(ret+=dfs(0,new_carry,0,1,new_sum))%=mod;if(allowcutb)(ret+=dfs(0,new_carry,1,0,new_sum))%=mod;if(allowcuta&&allowcutb)(ret+=dfs(0,new_carry,1,1,new_sum))%=mod;}else if(!cuta&&cutb){(ret+=dfs(0,new_carry,0,1,new_sum))%=mod;if(allowcuta)(ret+=dfs(0,new_carry,1,1,new_sum))%=mod;}else if(cuta&&!cutb){(ret+=dfs(0,new_carry,1,0,new_sum))%=mod;if(allowcutb)(ret+=dfs(0,new_carry,1,1,new_sum))%=mod;}else (ret+=dfs(0,new_carry,1,1,new_sum))%=mod;}}return f[k][carry][cuta][cutb][sum]=ret;
}
现在程序效率大大提高(大常数的 \(\Theta(n)\)),一秒跑 \(30000\) 毫无压力,只是常数有点大,跑 \(10^5\) 可能要两三秒。
正文部分结束了,接下来是吹水。
要不要把数据范围再开大一点,比如说 \(n \leq 10^9\) ,甚至 \(10^{18}\) ?
首先,虽然比较,但原来的记搜是可以改写成一般的递推形式的。
很抽象,但是可以看出来,这确实是一个 1D/0D 的动态规划,只是常数有一点大而已(迫真)。
进一步地,每一位最坏的情况就是 \(A,B\) 填 \(8\), \(C\) 填 \(6\),只会令 \(sum\) 减去 \(20\)。
换句话说,每个 \(sum\) 的转移只依赖于前 \(20\) 个状态,而且系数对于每个 \(sum\) 都是相同的。
有没有发现什么?
可以将 \(20 \times 2^4\) 个位置压在一起,用矩阵加速转移,理论复杂度是 \(320^3 \times \log n\) 左右。
稍微把时限放开点(或者机子比较快),跑 \(10^{24}\) 也许能冲一冲。
有点感慨,经过一系列优化,我们将原题 \(n=24\) 的数据范围一路加到了 \(n=10^{24}\)。
不能说这是算法竞赛的全部,只能说不断优化算法,就是算法竞赛最大的乐趣之一吧。
 上完课整的活
上完课整的活