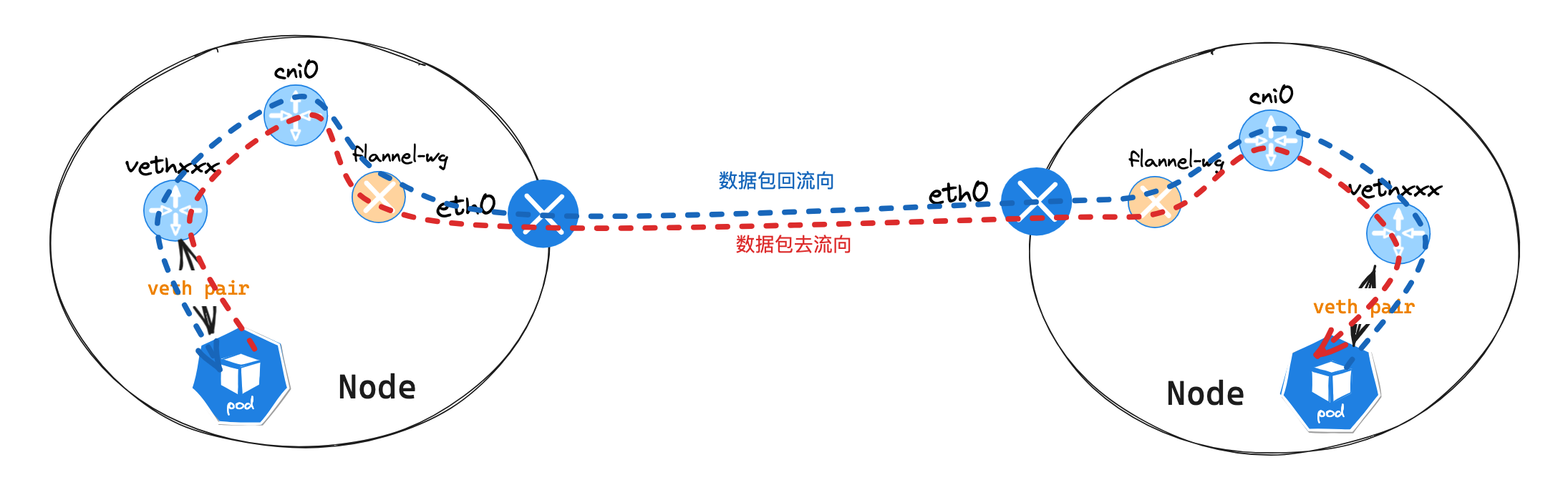
我们设 \(f[i][j]\)表示目前前 \(i\) 个宝箱的期望贡献的 \(j\) 次方。
根据题意可得 $f[i][k]=(f[i-1][1]+a[i])^k \cdot p[i]+(f[i-1][1]+b[i])^k \cdot (1-p[i]) $
这个式子很难处理,不妨用二项式定理优化
优化后式子则为:\(f[i][k]= \sum _{j=0}^{k} C_{k}^{j} \cdot f[i-1][j] \cdot a[i]^{k-j} \cdot p[i]+ \sum _{j=0}^{k}f[i-1][j] \cdot b[i]^{k-j} \cdot (1-p[i])\)
合并一下
\(f[i][k]= \sum _{j=0}^{k} C_{k}^{j} \cdot f[i-1][j] \cdot (a[i]^{k-j} \cdot p[i] +b[i]^{k-j} \cdot (1-p[i]) )\)
到这里我们就可以在 \(O(nk)\) 预处理\((a[i]^{k-j} \cdot p[i] +b[i]^{k-j} \cdot (1-p[i]) )\),再 \(O(nk^2)\) 转移了。
using namespace std;#define int long long
const int N=1e4+107;
const int mod=998244353;int n,k;
int p[N],a[N],b[N];int read()
{int f=1,s=0;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){s=(s<<1)+(s<<3)+(ch^48);ch=getchar();}return f*s;
}int qpow(int a,int b)
{int ans=1;while(b){if(b&1) ans=ans*a%mod;b=b>>1;a=a*a%mod;}return ans;
}int ans=0;
int fac[200],inv[N];
void init()
{fac[0]=inv[0]=1;for(int i=1;i<120;i++){fac[i]=fac[i-1]*i%mod;inv[i]=qpow(fac[i],mod-2);}
}int C(int n,int m){return fac[n]*inv[n-m]%mod*inv[m]%mod;}int f[N][120],tmp[N][120];
signed main()
{init();n=read(),k=read();for(int i=1;i<=n;i++){p[i]=read(),a[i]=read(),b[i]=read();}int sum=0;for(int i=1;i<=n;i++){tmp[i][0]=f[i][0]=1;for(int j=1;j<=k;j++){tmp[i][j]=(qpow(a[i],j)*p[i]%mod+qpow(b[i],j)*(1-p[i]+mod)%mod)%mod;}}for(int i=1;i<=k;i++){f[1][i]=tmp[1][i];}for(int i=2;i<=n;i++){for(int j=1;j<=k;j++){for(int g=0;g<=j;g++){f[i][j]=(f[i][j]+f[i-1][g]*C(j,g)%mod*tmp[i][j-g]%mod)%mod;}}}printf("%lld",f[n][k]);return 0;
}`