1.利用最大公约数求出一个约数
n和某个数的公约数一定是n的约数,即\(\forall k \in\mathbf{N}_{+},\gcd(k,n) \mid n\),只要选取适当的k使得\(1<\gcd(k,n)< n\),,就能够求得n的一个约数
满足这个条件的k很多,n的因数的大部分倍数都可行
我们通过\(f(x)=(x^2+c)\bmod n\)来生成一个序列\(\{x_i\}\):随机取一个\(x_1\),令\(x_2=f(x_1),x_3=f(x_2),\dots,x_i=f(x_{i-1})\),其中c是一个随机选取的常数
举个例子:
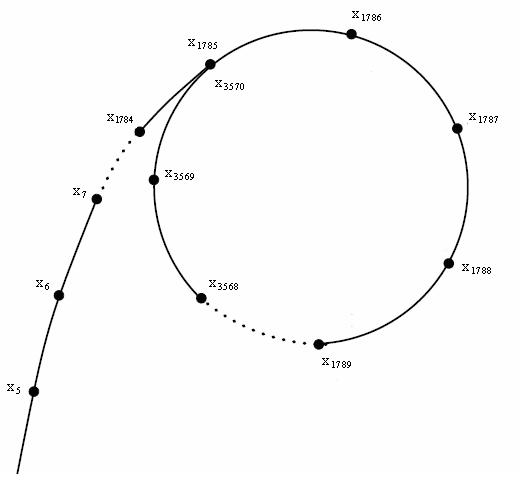
n=50,c=6,x_1=1,f(x) 生成的数据为:\(1, 7, 5, 31, 17, 45, 31, 17, 45, 31,\dots\)
可以发现在x以后,生成的数就在\(31,17,45\)之间循环了
如果将这些数如下图一样排列起来,会发现这个图像酷似一个\(\rho\),算法也因此得名 rho
该式子满足\(\forall x \equiv y(\bmod p), f(x)\equiv f(y)(\bmod p)\),其中\(p|n\)
证明:
若\(x\equiv y \pmod p\),则可以将它们表示为\(x=k_1p+a\),\(y=k_2p+a\),满足\(k_1,k_2,a\in \mathbb{Z},a\in \left[0,p\right)\)。
\(f(x)=(x^2+c) \bmod n\),因此\(f(x)=x^2+c-kn\),其中\(k \in \mathbb{Z}\)。\[\begin{aligned} f(x) & = x^2+c-kn\\ & = (k_1p+a)^2+c-kn\\ & = k_1^2 p^2+2k_1pa+a^2+c-kn\\ & \equiv a^2+c \pmod p \end{aligned} \]同理,\(f(y) \equiv a^2+c \pmod p\),因此\(f(x) \equiv f(y) \pmod p\)。