题目链接 : [Ynoi2011] 初始化
神仙trick + 卡常题,前缀后缀和根本没听过。
根号分治 + 分块。
对于修改操作,发现是跳着修改,考虑根号分治。
- 若\(x \ge \sqrt{n}\),直接暴力更改,复杂度\(O(\sqrt{n})\)。
- 反之,可以将序列抽象成一堆大小为\(x\)的段,如图,\(l,r\)是查询的区间。
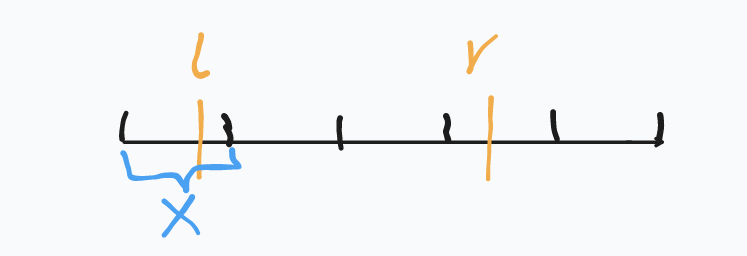
发现\(l\sim r\)中间的整块一定都会被修改到,但是散块会被部分修改。由于题面中有一个重要的性质\(y\le x\),所以\(y\)一定在第一块中。
记两个数组\(pre_{i,j}\)表示记录当以\(i\)为块长分割序列时,前\(j\)个位置被更改的前缀和,\(suf_{i,j}\)为后缀和。
对于一个查询\(l,r\),如果是整块,直接前缀和求差,如果不在同一块,那么直接求\(l\)到其所在块末的后缀和,\(r\)到其所在块的前缀和,还有中间整块的贡献。
由于常数原因,\(x\)的阈值不应设太大,实测大约120左右跑的最快,序列分块时的块长取\(\sqrt{n}\)即可。
本题并不卡常,cin/cout关了同步流就可过。
点此查看代码
#include<bits/stdc++.h>
#include<bits/extc++.h>
// using namespace __gnu_pbds;
// using namespace __gnu_cxx;
using namespace std;
#define infile(x) freopen(x,"r",stdin)
#define outfile(x) freopen(x,"w",stdout)
#define errfile(x) freopen(x,"w",stderr)
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;const int N = 2e5 + 10,M = 500,mod = 1e9 + 7;
inline void Mod(int &x){if(x > mod) x -= mod;}
int n,m,a[N],len,pos[N],L[M],R[M],sum[M],limit,pre[M][M],suf[M][M],siz;
inline void solve(){cin>>n>>m;for(int i = 1;i <= n; ++i) cin>>a[i];limit = 128;len = sqrt(n),siz = n/len;for(int i = 1;i <= siz; ++i) L[i] = R[i - 1] + 1,R[i] = L[i] + len - 1;if(R[siz] < n) siz++,L[siz] = R[siz - 1] + 1,R[siz] = n;for(int i = 1;i <= siz; ++i){for(int j = L[i];j <= R[i]; ++j){pos[j] = i;Mod((sum[i] += a[j]));}}auto update1 = [&](int x,int y,int z)-> void{for(int i = y;i <= n;i += x){Mod(a[i] += z);Mod(sum[pos[i]] += z);}};auto update2 = [&](int x,int y,int z) -> void{for(int i = x;i >= y; --i) Mod(pre[x][i] += z);for(int i = 1;i <= y; ++i) Mod(suf[x][i] += z);};auto Q = [&](int left,int right) -> int{int p = pos[left],q = pos[right],res = 0;if(p == q){for(int i = left;i <= right; ++i) Mod(res += a[i]);return res;}for(int i = left;i <= R[p]; ++i) Mod(res += a[i]);for(int i = L[q];i <= right; ++i) Mod(res += a[i]);for(int i = p + 1;i < q; ++i) Mod(res += sum[i]);return res;};auto query = [&](int left,int right) -> int{int res = Q(left,right);for(int i = 1;i < limit; ++i){const int p = (left - 1)/i+1,q = (right-1)/i+1;if(p == q){Mod(res += pre[i][(right-1)%i+1]);Mod((res -= pre[i][(left-1)%i]) += mod);}else{res = (res + (q - p - 1ll)*pre[i][i]%mod)%mod;Mod(res += pre[i][(right-1)%i+1]);Mod(res += suf[i][(left-1)%i+1]);}}return res;};for(int i = 1,op,l,r,x,y,z;i <= m; ++i){cin>>op;if(op^2){cin>>x>>y>>z;Mod(z);if(x >= limit) update1(x,y,z);else update2(x,y,z);}else{cin>>l>>r;cout<<query(l,r)<<'\n';}}
}
signed main(){cin.tie(nullptr)->sync_with_stdio(false);cout.tie(nullptr)->sync_with_stdio(false);solve();
}