link.
这种 RMQ 对像我这样萌新来说只有两种比较直观的方案:
- 线段树
- ST 表
首先考虑线段树,如果是朴素的一维线段树,那么我们只能一行一行地扫,显然相比暴力优化了一些,但不多,最终还是会愉快地 T 掉(亲测)。
然后我不会超冷门的数据结构二维线段树。
所以蒟蒻只能用好写的 ST 表了,只不过也是二维的。
开写!
首先观察一下样例(事实证明有时样例是很重要的),我们发现它并没有按照题目描述读入:
1 2 3 4 5 6
7 8 9 0
实际上它是这么读的:
1
2 3
4 5 6
7 8 9 0
也就是说我们读入的和需要查询的其实都是一个等腰直角三角形。
那么我们按照惯用套路,设 \(st_{i,j,k}\) 表示以第 \(i\) 行第 \(j\) 列的点为上顶点的直角边长是 \(2^k\) 的三角形区域内的最大值,那么它的两条直角边分别是 \(i\rightarrow i+2^k-1\) 和 \(j\rightarrow j+2^k-1\)。
然后我们像平常一样再次发现了问题:
我们的普通二维 ST 表是针对矩形(准确来说应该是正方形)而言的,我们发现一个 \(st_{i,j,k}\) 的矩形可以恰好由 \(st_{i,j,k-1}\)、\(st_{i,j+2^{k-1},k-1}\)、\(st_{i+2^{k-1},j,k-1}\) 和 \(st_{i+2^{k-1},j+2^{k-1},k-1}\) 四个已经算过的矩形构成,如图所示:

但是对于三角形来说我们可就没有这么幸运了:

我们发现一个 \(st_{i,j,k}\) 的等腰直角三角形无法由 \(st_{i,j,k-1}\)、\(st_{i+2^{k-1},j,k-1}\) 和 \(st_{i+2^{k-1},j+2^{k-1},k-1}\) 三个三角形契合起来,我们会留下中间一个灰色区域。
怎么办?我们尝试在原来的大三角形的底边正中间处再放置一个边长是 \(2^{k-1}\) 的三角形,这个三角形可以用 \(st_{i+2^{k-1},j+2^{k-2},k-1}\) 来表示(我标红的那一段正好是大三角形的底边长的 \(\frac{1}{4}\)):

但是好像还没有覆盖全?那就再在原三角形的另一条直角边和斜边的正中间再加一个吧!

此时我们就覆盖完全了,另外添加的那两个三角形可以用 \(st_{i+2^{k-2},j,k-1}\) 和 \(st_{i+2^{k-2},j+2^{k-2},k-1}\) 表示。
不难证明 \(\forall \frac{n}{2}\le m<n\),一个边长是 \(n\) 的三角形都可以由不多于 \(6\) 个边长是 \(m\) 的三角形完全覆盖。
由于我们解决的是可重复贡献问题,我们直接用这 \(6\) 个三角形更新大的即可。
为了避免没用的循环,我们只需要枚举到满足 \(2^k\le h\) 的最大的 \(k\) 即可(\(h\) 是我们需要查询的边长)。
注意到需要查询的 \(h\) 是一定的,也就是 \(k\) 是一定的,因为你不这么干会 MLE,所以可以把 st 数组滚动起来,最后枚举 \(k\) 的维只开到 \(2\) 即可。
于是就有了预处理部分的代码:
read (n) ,read (h) ;
f (i ,1 ,n ,1) {f (j ,1 ,i ,1) {read (st[i][j][0]) ;}
}
for (int i = 0 ; ;i ++) {if (h >= (1 << i)) k = i ;else break ;
} // 找到最大的 k
f (t ,1 ,k ,1) {int u = t & 1 ,v = u ^ 1 ; // 分奇偶性讨论即可,注意奇数的上一个状态是偶数,反之亦然,那么 u 就是当前状态,v 是上一个状态f (i ,1 ,n - (1 << t) + 1 ,1) {f (j ,1 ,i ,1) {st[i][j][u] = max (st[i][j][v] ,max (st[i + (1 << t - 1)][j][v] ,st[i + (1 << t - 1)][j + (1 << t - 1)][v])) ;if (t > 1) { // <= 1 的时候没必要st[i][j][u] = max (st[i][j][u] ,max (st[i + (1 << t - 1)][j + (1 << t - 2)][v] ,max (st[i + (1 << t - 2)][j][v] ,st[i + (1 << t - 2)][j + (1 << t - 2)][v]))) ;}}}
}
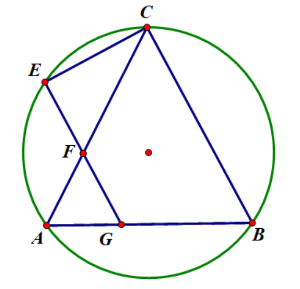
接下来就是查询部分,思路基本一致,但是注意到 \(h\) 不一定是 \(2\) 的正整数次幂,所以添加的三个三角形不再能直接表示为上面那样了,我们注意到我们添加的三个三角形都是在边的正中间的,那么我们来推到一下到底该怎么表示,以大三角形下面那个为例:

我们可以知道 \(1\) 号边减 \(2\) 号边等于 \(\frac{h-2^k}{2}\),由于我们作的是中垂线,那么 \(1\) 号减 \(2\) 号就等于 \(3\) 号减 \(4\) 号,得 \(5\) 号的长是 \(\frac{h-2^k}{2}\),也就是说我们添加的(红色的那个)三角形的顶点距离侧面的那条直角边的距离是 \(\frac{h-2^k}{2}\),那么它可以用 \(st_{i+h-1-2^k+1,j+\frac{h-2^k}{2},k-1}\) 来表示(\((i,j)\) 是大三角形的上顶点)。
同理可以得到其他两个三角形的表示。
那么我们的查询:
inline int query (int x ,int y) {int _ = x + h - 1 ,__ = y + h - 1 ;int u = k & 1 ; // 求出 k 对应的第三为下标int ans = max (st[x][y][u] ,max (st[_ - (1 << k) + 1][y][u] ,st[_ - (1 << k) + 1][__ - (1 << k) + 1][u])) ; // 正常的 ST 表查询操作if (k <= 1) return ans ; // 没必要在加那三个三角形了int t = (h - (1 << k)) >> 1 ;ans = max (ans ,max (st[_ - (1 << k) + 1][y + t][u] ,max (st[x + t][y][u] ,st[x + t][y + t][u]))) ; // 就是上面我说的那个return ans ;
}