反射容斥
一层反射:有一条线 \(y=x+b\) 不能碰到。
从第一次碰到直线开始,将后面的部分沿直线翻折,最终一定会到达 \((n-b,n+b)\),因为 \(b\ne 0\),所以构成双射。答案即为 \(\binom{2n}{n}-\binom{2n}{n-b}\)。
注意,如果最终到达的位置是 \((n,m)\),反射后 \(n,m\) 会互换,答案为 \(\binom{n+m}{m}-\binom{n+m}{n-1}\)。
卡特兰数
将左括号看作向右,右括号看作向上,则等价于不能碰到 \(y=x+1\),故卡特兰数有组合意义:\(\binom{2n}{n}-\binom{2n}{n-1}\)。
二层反射容斥
每一次碰到线后记录 AAABBBAABBABA的形式,相邻的合并,得到ABABAB的形式,容斥即可,正确性地方太小。
设第一条线为 \(y_1=x+l,y_2=x+r\),\(l<0<r\),那么有答案:
注意:\(k\in \Z\),只需要求组合数有意义即算入答案。
P3266 [JLOI2015] 骗我呢
求有多少个 \(n\times m\) 的数组,满足 \(x_{i,j}<x_{i,j+1},x_{i,j}<x_{i-1,j+1}\),每个位置可以填 \([0,m]\) 的数。
\(n,m\le 10^6\)。
容易观察到每一行都是递增的,而且每一行都恰好少一个数,且少的这个数是单调递增的,我们可以直接列 DP 方程。
设 \(dp_{i,j}\) 表示第 \(i\) 行少的数是 \(j\),有:
是形式上非常简洁的 DP,系数均为 \(1\),但不能进行任何数据结构优化。我们考虑放在网格图上计数
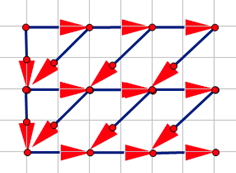
注意到只有第一列有直上直下的转移,这是因为 \(dp_{i,0}=1\)。
我们从第二行开始,每一行在上一行的基础上向右平移一格,就可以得到标准的转移:
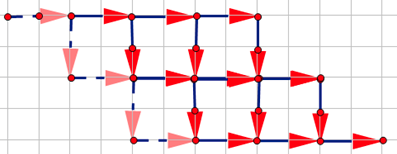
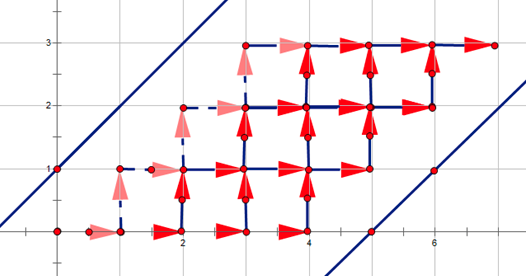
发现相当于不能碰直线 \(y_1=x+1\),\(y_2=x-(m+2)\)。
#include <bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define fi first
#define se second
using namespace std;
int read(){char c=getchar();int h=0,tag=1;while(!isdigit(c)) tag=(c=='-'?-1:1),c=getchar();while(isdigit(c)) h=(h<<1)+(h<<3)+(c^48),c=getchar();return h*tag;
}
void fil(){freopen("data.in","r",stdin);freopen("data.out","w",stdout);
}
const int mod=1e9+7;
const int N=3e6+5;
int fac[N],inv[N];
int ksm(int a,int b) {if(b==1) return a%mod;int s=ksm(a,b/2);s=s*s%mod;if(b%2==1) s=s*a%mod;return s%mod;
}
int binom(int n,int m) {if(m<0||n<m) return 0;return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
signed main(){
// fil();int n=read(),m=read();int l=-m-2,r=1;int _n=n+m+1,_m=n;inv[0]=1,fac[0]=1;for(int i=1;i<=N-100;i++) fac[i]=fac[i-1]*i%mod,inv[i]=ksm(fac[i],mod-2)%mod; int ans=0;for(int i=-1000000;i<=N;i++) {if(_n-i*(r-l)+r>(_n+_m)) continue;if(_n-i*(r-l)<0) break;ans+=binom(_n+_m,_n-i*(r-l))-binom(_n+_m,_n-i*(r-l)+r);ans=(ans+mod)%mod;}cout<<ans<<endl;return 0;
}