DATE #:20240827
ITEM #:DOC
WEEK #:TUESDAY
DAIL #:捌月廿肆
``` 渊沉鳞潜,冻血锈骨闭魂眼;披风游焰,穿峡掠谷骋日月。 ```TAGS
< BGM = "Dragonflame--Kirara Magic" > < theme = oi-contest > < theme = oi-data structure Segment > < [空] > < [空] >
又是抽象模拟赛啊
前一个小时甚至有题没有数据
T1A. 本质不同GCD
时间限制: 2 s 内存限制: 512 MB 测评类型: 传统型
题目描述
给定 \(L,R,k\) ,询问本质不同的数字 \(x\) 的个数,使得存在 \(L \le a_1,a_2,\dots,a_k \le R\) ,满足 \(\gcd(a_1,a_2,\dots,a_k)=x\) 。
其中 \(a_i\) 可以互相重复。
输入格式
一行三个整数 \(L,R,k\) 。
输出格式
一行一个整数$ ,表示答案。
样例输入1
2 3 2样例输出1
3样例解释1
\(\gcd(2,2)=2,\gcd(2,3)=1,\gcd(3,3)=3\) 。
数据范围及提示
对于 \(20 \%\) 的数据,保证 \(R \le 10, k \le 6\) 。
对于 \(40 \%\) 的数据,保证 \(R \le 3 \times 10^6,k \le 6\) 。
对于额外 \(20 \%\) 的数据,保证$ 。
对于所有 \(100 \%\) 的数据,保证 \(1 \le L \le R \le 10^{10},1 \le k \le 13\) 。
//2024.8.27
//by white_ice
#include<bits/stdc++.h>
//#include"need.cpp"
using namespace std;
#define itn long long
#define int long long
constexpr itn oo = 1000000;
itn l,r,k;
int out;
main(void){//fre();cin.tie(0)->sync_with_stdio(0);cin >> l >> r >> k;if (l==702983183){cout << 10000000000 << endl;exit (0);}if (k<=1||l==1){cout << (r-l+1) << '\n' << flush;exit (0);}for (int i=1;i<l;i++){int p = (l-1)/i;itn u = (p+1)*i;if (u+i<=r) out++; if (r-l+1<i)break;}//p_(r-l+1);cout << (r-l+1+out) << '\n' << flush;exit (0);
}我这个SB答案特判就别看了
首先\(L-R\)中没有疑问,一定是都能取到的
T2B.木门道伏击战 (intercept)
时间限制: 1 s 内存限制: 256 MB 测评类型: 传统型
【题目背景】
建兴九年( 231年), 诸葛亮 率蜀军 四出祁山 。 司马懿料到蜀军粮草不济,坚守不出,又命人在成都散布诸葛亮欲谋反的谣言。刘禅听信谣言,下旨命诸葛亮退兵。在退兵时,魏军决定追击,诸葛亮早有防备,在木门道 伏击 射杀张郃。
【题目描述】
小 W在《三国演义》中读到四出祁山,对此非常感兴趣,在思考这场战役时他想出了一个问题。
小 W认为蜀军共有 N处伏击地点,可以把这 N个伏击地点从 1到 N进行标号 ,且蜀军恰好有 M个兵种 。 由于伏击需要保证军队可以方便地调度,所以不存在连续 M个伏击地点埋伏了 M个 不同的 兵种。小 W想知道所有 不同的 埋伏方案数对 1e9+7取模。
【输入格式】
从文件intercept.in中读入数据。
一行一 个数 N。
【输出格式】
输出到文件intercept.out中。
一行一个数,表示结果对1e9+7取模的结果。
【样例输入1】
3 3
【样例输出1】
21
【样例输入2】
见下发文件
intercept.in。
【样例输出2】
见下发文件
intercept.out。
【数据范围】
对于8%的数据, m=2
对于另16%的数据, n<=10,m<=4
对于48%的数据, n<=100000,m<=10
对于80%的数据, n<=100000,2<=m<=100
对于100%的数据, 2<=m<=100,m<=n<=10^16
//2024.8.27
//by white_ice
#include<bits/stdc++.h>
//#include"need.cpp"
using namespace std;
#define int long long
#define itn long long
constexpr int oo = 105;
constexpr int mod = 1e9+7;
int n,m;
struct matrix{int f[oo][oo];
matrix(){for(int i=0;i<oo;i++)for(int j=0;j<oo;j++)f[i][j] = 0;}
__inline matrix operator*(matrix b){matrix c;for(int i=1;i<=m;i++)for(int j=1;j<=m;j++){c.f[i][j]=0;for(int k=1;k<=m;k++)c.f[i][j]=(c.f[i][j]+f[i][k]*b.f[k][j]%mod)%mod;}return c;}}st;
__inline matrix qpow(matrix a,int b){matrix ans;for(int i=1;i<oo;i++)ans.f[i][i]=1;while(b){if(b&1)ans = ans*a;a = a*a;b>>=1;}return ans;}
main(void){//fre();cin >> n >> m;for(int i=1;i<=m;i++)for(int j=1;j<=m;j++){if(i-1==j) st.f[i][j]=m-(j-1);else if(i==1) st.f[i][j]=0;else if(i<=j) st.f[i][j]=1;}matrix ans = qpow(st,n);itn out = 0;for(int i=1;i<=m;i++){//p_(true,out,ans.f[i][1]);out=(out+ans.f[i][1])%mod;}cout << out << '\n' << flush;exit (0);
}考虑DP,我们设\(f_{i,j}\)表示遍历到第i位时,最后有j个元素互不相同,
那么状态转移就很好写了啊
其中第二维只有100位,
矩阵快速幂优化即可
T3C. 向日葵覆盖(ywk)
时间限制: 2 s 内存限制: 512 MB 测评类型: 传统型
一共有 \(n\) 个巨型向日葵,小 I 把这些向日葵栽到了地上,第 \(i\) 个向日葵高度为 \(a_i - i\),特别的如果 \(a_i - i \leq 0\) 那说明这个向日葵长在地底下。所有长在地上的向日葵可以遮盖住 \([i, a_i]\),为了更好的种植向日葵,小 I 想知道 \([l,r]\) 内第一个没有被覆盖的整数位置是哪里。糟糕的是 小 I 发现向日葵的高度会变化,所以他需要支持修改向日葵的高度和查询区间 \([l,r]\) 内第一个没有被覆盖的整数位置。
先发一下形式化题面。
给定一个长度为 \(n\) 的序列 \(a\) , 分别为 \(a_1, a_2 , ... a_n\) 。 你需要支持 \(m\) 次操作,操作有以下两种.
- 给定 \(x, v\) , 把 \(a_x\) 变成 \(v\)。
- 给定 \(l, r\) , 求最小的 \(x\in [l,r]\) 满足 \(\max_{i=l}^{x}a_i \leq x\). 如果不存在一个合法的 \(x\) 输出 \(-1\).
\(1 \leq n, m, a_i \leq 10^6\) , 强制在线(但是出题人懒得造了,靠大家自觉)
这题大家都能做到 \(O(n^2)\) 所以先不设置部分分了
输入样例
5 5 2 1 3 4 5 2 1 5 2 2 4 1 3 5 1 2 3 2 1 5输出样例
2 2 5
//2024.8.27
//by white_ice
//#1736. 向日葵覆盖(ywk)
//单侧递归线段树
#include<bits/stdc++.h>
//#include"need.cpp"
using namespace std;
constexpr int inf=1e9;
constexpr int oo=1e6+5;
constexpr int op=3e6+10;
int n,m;int st[oo];
int ans,mxx;
struct segment{int ls[op],rs[op],tot,rt;int f[op],mx[op];int work(int nl,int ns,int u,int lx){if(nl==ns) {return(max(lx,mx[u])<=nl?nl:inf);}int mid=(nl+ns)>>1;if(lx<=mid) return min(work(nl,mid,ls[u],lx),f[rs[u]]);else return work(mid+1,ns,rs[u],max(lx,mx[ls[u]]));}void up(int u,int nl,int ns){mx[u]=max(mx[ls[u]],mx[rs[u]]);int mid=(nl+ns)>>1;if(mx[ls[u]]<=mid) f[rs[u]]=mid+1;else f[rs[u]]=work(mid+1,ns,rs[u],mx[ls[u]]);}void build(int nl,int ns,int &u){u=++tot;if(nl==ns){mx[u]=st[nl];f[u]=(st[nl]<=nl? nl: inf);return;}int mid=(nl+ns)>>1;build(nl,mid,ls[u]);build(mid+1,ns,rs[u]);up(u,nl,ns);}void update(int nl,int ns,int u,int x){if(nl==ns){mx[u]=st[nl];f[u]=(st[nl]<=nl? nl: inf);return;}int mid=(nl+ns)>>1;if(x<=mid) update(nl,mid,ls[u],x);else update(mid+1,ns,rs[u],x);up(u,nl,ns);}void query(int l,int r,int nl,int ns,int u){if(l<=nl&&ns<=r){ans=min(ans,work(nl,ns,u,mxx));mxx=max(mxx,mx[u]);return;}int mid=(nl+ns)>>1;if(l<=mid) query(l,r,nl,mid,ls[u]);if(r>mid) query(l,r,mid+1,ns,rs[u]);}
}seg;
main(void){//fre();cin.tie(0)->ios::sync_with_stdio(0);cin >> n >> m;for(int i=1;i<=n;i++) cin>>st[i];seg.build(1,n,seg.rt);for(int op,x,y,i=1;i<=m;i++){cin >> op >> x >> y;if(op==1){st[x]=y;seg.update(1,n,seg.rt,x);}else{ans=inf;mxx=0;seg.query(x,y,1,n,seg.rt);cout<<(ans>=inf?-1:ans)<<'\n';}}exit (0);
}
蘑菇覆盖题解
发现要求最小的
\(x \in [l,r]\) 满足 \(\max_{i=l}^{x}a_i\leq x\) , 可以想到用类似于兔队线段树的做法来解决这个问题。因为修改是单点修改,查询也完全可以看成是几个节点信息的合并,所以关键在于如何处理好 update 操作。考虑在线段树的每个节点上维护这个节点所代表的区间 \([l,r]\) 内的最小的满足 \(\max_{i=l}^{x}a_i\leq x\) 的 \(x\) . 显然在 update 操作中这个节点左边的其它节点可能会对这个节点产生一些影响,所以这里记 \(update(u, l, r, lmax)\) , \(u\) 表示当前要 update 的节点的编号\(l\) 和\(r\) 表示当前节点所代表的区间,\(lmax\) 表示在当前节点左边有一个大小为 \(lmax\) 的值对 update 产生影响。考虑分类讨论。
- \(lmax > mid\) ,那么 \([l, mid]\) 中就不可能有满足条件的 \(x\) 了,考虑右区间就行,即 \(update(rs, mid + 1, r, \max(lmax, Max_{ls}))\) 这里的 \(Max_{ls}\) 表示左儿子所代表区间内
\(a_i\) 的最大值。 - \(lmax < mid\) ,那么 \([mid + 1, r]\) 只会受到左儿子的影响,这个东西可以记录一下叫 \(ans2\)。那么原来的 update 就相当于 \(\min(update(ls, l, mid, lmax), ans2_{rs})\)
至于这个 \(ans2\) 怎么处理,其实他就是 \(update(rs, mid + 1, r, Max_{ls})\)
T4D. 【2023.6.13 ywk 互测】机关
时间限制: 1 s 内存限制: 512 MB 测评类型: 传统型
饺子哥哥是天上神仙, 祂用魔法包了好多好多饺子,一共有 \(n\) 饺子,并且在一号饺子里放了一枚硬币。小橘子是饺子哥哥养的一只猫猫.它想得到那枚硬币。只要它通过饺子哥哥设计的游戏,就能拿到硬币。游戏如下:
聪明的饺子哥哥设计了一个机关,并把饺子放在了机关里。机关有四个按钮,机关内部有两个序列 \(a, b\) ,四种按钮的作用分别是:
- 若这是第 \(i\) 次按动 \(1\) 或者 2\(2\) 按钮,则将饺子 \(i\) 放入 \(a\) 序列的前端。
- 若这是第 \(i\) 次按动 \(1\) 或者 2\(2\) 按钮,则将饺子 \(i\) 放入 \(a\) 序列的末端。
- 将 \(a\) 序列开头的饺子取出,并放入 b\(b\) 序列末尾。
- 将 \(a\) 序列末尾的饺子取出,并放入 b\(b\) 序列末尾。
机关很特别,只要按动 \(3\) 或 \(4\) 号按钮,\(1\) 和 \(2\) 号按钮将永远消失。
小橘子需要恰好按动 \(n\) 次 \(3\) 或者 \(4\) 号按钮,得到长度为 \(n\) 的 \(b\) 序列,此时小橘子可以拿到 \(b\) 序列第 \(k\) 个位置的饺子。
当然作为饺子哥哥的猫猫,聪明的小橘子可以轻松拿到硬币,但它想考考你,它会给你一组 \(n, k\) , 问有多少个不同的合法 \(b\) 序列可以使它得到硬币。聪明的小朋友,你能回答出小橘子的问题吗?
注:1.我们称 \(b\) 序列为合法的,当且仅当可以由上述操作生成;
2.由于答案很大,小橘子会给你一个数 \(mod\) ,你只需要输出答案对 \(mod\) 取模的值。
输入格式
输入仅一行三个数表示 \(n,k,mod\)
输出格式
输出仅一行一个数,表示答案。
数据范围
对于8%的数据,\(k \leq n \leq 10\);
另有20%的数据,\(k=n\);
对于60%的数据,\(k \leq n \leq 3000\);
另有12%的数据,\(k=1\);
对于100%的数据,\(k \leq n \leq 500000,10^8 \leq mod \leq 2\times 10^9\) 且是质数
输入样例
输入样例1: 2 1 998244353 输入样例2: 3 2 998244353 输入样例3: 10 5 998244353输出样例
输出样例1: 1 输出样例2: 2 输出样例3: 6864样例解释
样例解释1:
合法的 b 序列为{1,2},一种合法的生成方式是{1,2,3,3}:
样例解释2:
合法的 \(b\) 序列为\(\{2,1,3\},\{3,1,2\}\)
分别对应可能的生成方式是\(\{2,1,2,3,3,3\}\),\(\{2,1,2,4,4,3\}\)
//2024.8.27
//by white_ice
//#2204. 【2023.6.13 ywk 互测】机关
//计数,组合数学
#include<bits/stdc++.h>
//#include"need.cpp"
using namespace std;
#define itn long long
#define int long long
constexpr int oo = 1e6+10;
int fac[oo],ifac[oo],inv[oo];
int pow2[oo];int n,k,mod;
int add(int x,int y){return x+y>=mod?x+y-mod:x+y;}
__inline int getc(int n,int m){if (n<m||m<0) return 0;return fac[n]*ifac[n-m]%mod*ifac[m]%mod;
}
__inline int qpow(int a,int b=mod-2){int res = 1;while (b){if(b&1)(res*=a)%=mod;(a*=a)%=mod;b>>=1;}return res;}
main(void){//fre();cin.tie(0)->ios::sync_with_stdio(0);cin >> n >> k >> mod;ifac[1] = ifac[0] = fac[0] = fac[1] = inv[1] = 1;pow2[0] = 1;pow2[1] = 2;for (int i=2;i<=2*n;++i){fac[i] = fac[i-1]*i%mod;inv[i] = (mod-mod/i)*inv[mod%i]%mod;ifac[i] = ifac[i-1]*inv[i]%mod;pow2[i] = pow2[i-1]*2%mod;}int res = 0;if (n==k){cout << getc(2*n-2,n-1)*inv[n]%mod << '\n';exit (0);}for (int i=n-k+1;i<=n;++i){int j = i-(n-k);res = add(res,getc(i-2,n-k-1)*pow2[n-k-1]%mod*add(getc(k-j+k-1,k-1),mod-getc(k+k-j-1,k))%mod);}cout << res << '\n';exit (0);
}
声明:本题解100%基于youwike讲解内容,若有不解之处请移步向youwike询问,因为我也不会
题意简明:
给定一个\(1-n\)的排列以及A,B两个空序列,现定义如下四个操作:
- 将原序列中队首元素取出,加入A前端
- 将原序列中队首元素取出,加入A末端
- 将A中队首元素取出,加入B末端
- 将A中队尾元素取出,加入B末端
要求在使用3或4操作后,不能再使用1或2操作
求解共多少种操作方法可使B序列长度为n的情况下,的k项为1
题解正文:
首先考虑按照题目中的操作方式,
要保证B长度为n,就要先将原序列使用1,2操作清空
在只进行1,2操作时,最终A序列一定会形成一个向下凹的情况
类似:

这里顺便吐槽一下youwike的古神画风
其中最低点就是1,是我们要取到的地方
那么下面可以开始考虑,如何将这个序列A通过3,4操作变成需要的B
这里我们假设1是从左边取到的,那么就会这样:
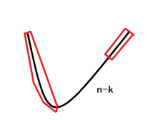
其中红色的部分为要加入B的前\(k\)个,没有被取到的则剩下\(n-k\)个
注意到,剩余\(n-k\)个可以随意加入,所以可以不考虑这些,加入这些共有\(2^{n-k-1}\)种可能,
将前面的方案数最后乘上\(2^{n-k-1}\)即可
下面对B的前\(k\)项进行讨论
由于序列A向下凹陷的特殊性质,我们不难理解,加入B的前\(k\)项一定是以两个严格下降子序列构成的
那么问题就被转化成了有多少长度为\(k\)的序列,可以被表示为两个单调递减的子序列
单调递减也可以反过来求单调递增,所以这里我们求单调递增
首先,我们引入一个引理:
一个序列能被表示为两个单调递增子序列,那么一定能够保证一个子序列无时无刻都大于另一个子序列
为什么呢?看图:
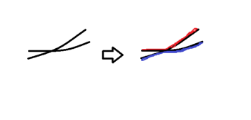
很难不发现,如果出现了左边这样的情况,我们完全可以转化成右边这样的
下面考虑DP,我们设定较大序列为\(x\),较小序列为\(y\)
我们定义\(f_{i,j}\),表示考虑到第\(i\)个数时,序列\(x\)的最后一个值为\(j\)
首先,\(f_{i,j}\)可以将当前一个最小的数加入到\(y\)中,即向\(f_{i+1,j}\)转移
同时,\(f_{i,j}\)也可以向\(f_{i,j+1},f_{i,j+2},....\)转移
当然,这里要注意,\(j\ge i\)是限制条件
然后,我们就发现,这个DP过程其实就是一个格路计数
具体嘛。。。看图:
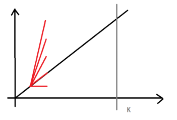
在如图这样一张网格里,从起点\((1,1)\)出发,图中红线为合法转移方式,问最终到达横坐标为k的方案数
其中直线\(y=x\)不可跨越
那么转移实际上可以转化为向右和向上两种简单操作,使用反射容斥即可
关于反射容斥
我们考虑在一个网格中,从某一点走向另一点,同时网格上有一条不能跨越的直线
首先随意走,不考虑限制,那么总方案数是\(\begin{pmatrix}n+m\\n\end{pmatrix}\)
下面考虑不合法方案,不合法方案中总会有一个点和不能跨域的直线相交,我们找到第一个和该直线相交的点,并且将之前没经过这条直线的部分沿着该直线翻折
那么就会出现新的起点,计算新起点到原终点的路径数,用\(\begin{pmatrix}n+m\\n\end{pmatrix}\)减去即可
代码部分:
这里我们将youwike的代码直接复制过来,反正是他讲的题
/*\ | ^ ^ \-- | # # \\_| \
*/
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <vector>
#define int long longconst int N = 1e6 + 10;
int fac[N], ifac[N], inv[N];
int pow2[N];
int n, k, mod;int add(int x, int y) {return x + y >= mod ? x + y - mod : x + y;
}int C(int n, int m) {if (n < m || m < 0) return 0;return 1ll * fac[n] * ifac[n - m] % mod * ifac[m] % mod;
}int qpow(int a, int b = mod - 2) {int res = 1;while (b) {if (b & 1) res = 1ll * res * a % mod;a = 1ll * a * a % mod;b >>= 1;}return res;
}signed main() {std::ios::sync_with_stdio();std::cin.tie(0), std::cout.tie(0);std::cin >> n >> k >> mod;ifac[1] = ifac[0] = fac[0] = fac[1] = inv[1] = 1;pow2[0] = 1, pow2[1] = 2;for (int i = 2; i <= 2 * n; ++i) {fac[i] = 1ll * fac[i - 1] * i % mod;inv[i] = 1ll * (mod - mod / i) * inv[mod % i] % mod;ifac[i] = 1ll * ifac[i - 1] * inv[i] % mod;pow2[i] = 1ll * pow2[i - 1] * 2 % mod;}int res = 0;if (n == k) {std::cout << 1ll * C(2 * n - 2, n - 1) * inv[n] % mod << '\n';return 0;}for (int i = n - k + 1; i <= n; ++i) {int j = i - (n - k);res = add(res, 1ll * C(i - 2, n - k - 1) * pow2[n - k - 1] % mod * add(C(k - j + k - 1, k - 1), mod - C(k + k - j - 1, k)) % mod);}
// res = add(res, 1ll * C(n - 2, n - k - 1) * pow2[n - k - 1] % mod);std::cout << res << '\n';return 0;
}
后记:
这道题难度个人感觉还是挺大的,很多转化需要一些神奇的思路和经验,然后就是模拟赛别出这么抽象了,最少给个样例啊
单侧递归线段树(兔队线段树)
单侧递归线段树用于求解严格前缀最大值类问题
我们使用线段树进行维护
考虑将每个节点同时记录两个值,\(s_i,g_i\)
其中\(s_1\)表示正常线段树所记录的区间最大值,而\(g_i\)表示整体前缀的最大值
发现,在维护\(g_i\)时,直接将两颗子树的信息相加是错误的
左子树信息可以继承,但右子树不可以
那么我们考虑引入一个新函数\(calc(i,pre)\)它的作用是返回 \(i\) 子树内,考虑了前缀最大值 \(pre\) 的影响后的答案。
为了方便表述,把信息 1 记做 max[i],把信息 2 记做 cnt[i]
当当前节点 \(i\) 是叶节点的时候,贡献很容易计算。
否则考虑左右子树的贡献分别计算,分成两种情况考虑:
- \(pre\) 小于左子树的最大值:
此时对右子树来说,\(pre\) 是无意义的,所以递归进左子树,右子树的贡献直接用“全部”减“左子树”计算即可。 - \(pre\) 大于等于左子树的最大值:
此时对左子树来说,就不可能贡献任何前缀最大值了,所以贡献为 \(0\),然后递归进右子树即可。
可以看出,调用一次 \(calc\) 函数递归的时间复杂度为 \(O(logn)\),因为每次只递归进一个孩子。
每次维护当前节点的答案时,只要令 \(cnt[i]=cnt[leftchild[i]]+calc(rightchild[i],max[leftchild[i]])\) 即可。
可以发现有 \(O(logn)\) 个节点要调用 \(calc\) 函数,所以一次单点修改的时间复杂度为 \(O(log^2n)\)。
P4198 楼房重建
楼房重建
题目描述
小 A 的楼房外有一大片施工工地,工地上有 \(N\) 栋待建的楼房。每天,这片工地上的房子拆了又建、建了又拆。他经常无聊地看着窗外发呆,数自己能够看到多少栋房子。
为了简化问题,我们考虑这些事件发生在一个二维平面上。小 A 在平面上 \((0,0)\) 点的位置,第 \(i\) 栋楼房可以用一条连接 \((i,0)\) 和 \((i,H_i)\) 的线段表示,其中 \(H_i\) 为第 \(i\) 栋楼房的高度。如果这栋楼房上任何一个高度大于 \(0\) 的点与 \((0,0)\) 的连线没有与之前的线段相交,那么这栋楼房就被认为是可见的。
施工队的建造总共进行了 \(M\) 天。初始时,所有楼房都还没有开始建造,它们的高度均为 \(0\)。在第 \(i\) 天,建筑队将会将横坐标为 \(X_i\) 的房屋的高度变为 \(Y_i\)(高度可以比原来大—修建,也可以比原来小—拆除,甚至可以保持不变—建筑队这天什么事也没做)。请你帮小 A 数数每天在建筑队完工之后,他能看到多少栋楼房?
输入格式
第一行两个正整数 \(N,M\)。
接下来 \(M\) 行,每行两个正整数 \(X_i,Y_i\)。
输出格式
\(M\) 行,第 \(i\) 行一个整数表示第 \(i\) 天过后小 A 能看到的楼房有多少栋。
样例 #1
样例输入 #1
3 4 2 4 3 6 1 1000000000 1 1样例输出 #1
1 1 1 2提示
对于 \(100\%\) 的数据,\(1 \le X_i \le N\),\(1 \le Y_i \le 10^9\),\(1\le N,M \le 10^5\)。
//2024.5.16
//by white_ice
//P4198 楼房重建
#include <algorithm>
#include<bits/stdc++.h>
using namespace std;
#define itn long long
#define int long long
constexpr int oo = 100005;template <class usd>
bool jntm(usd a,usd b){return a>b?a:b;}
template <class usd>
bool ngm (usd a,usd b){return a<b?a:b;}int n,m;
double st[oo];namespace Tree{itn ls(itn a){return a<<1;}itn rs(int a){return a<<1|1;}itn mid(itn a,itn b){return (a+b)>>1;}struct nod{double v;itn len;}tree[oo<<2];void push(int x){tree[x].v=max(tree[x<<1].v,tree[x<<1|1].v);}int push_main(double lx,int x,int l,int r){ if(tree[x].v<=lx)return 0;if(st[l]>lx)return tree[x].len; if(l==r)return st[l]>lx;int m=mid(l,r);if(tree[ls(x)].v<=lx)return push_main(lx,rs(x),m+1,r);else return push_main(lx,ls(x),l,m)+tree[x].len-tree[ls(x)].len;}void find(int x,int l,int r,int to,int c){if(l==r&&l==to){tree[x].v=(double)c/to;tree[x].len=1;return ;}int mid=(l+r)>>1;if(to<=mid) find(x<<1,l,mid,to,c);else if(to>mid) find(x<<1|1,mid+1,r,to,c);push(x);tree[x].len=tree[ls(x)].len+push_main(tree[x<<1].v,x<<1|1,mid+1,r);}
};signed main(){ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);cin >>n >> m;using namespace Tree;int x,y;for (int i=1;i<=m;i++){cin >> x >> y;st[x] = (double)y/x;find(1,1,n,x,y);cout << tree[1].len<< '\n';}return 0;
}