AT cf17 final J Tree MST

AT cf17 final J Tree MST

考场上想出的黑题，然而写挂了……

思路

考场推出 boruvka 算法，会的直接跳过就好。

结论：一个点向另外一个点连出的最小边，一定在最小生成树上。

证明：参考 Kruskal 生成树的流程，若当前边（最小边）不在最小生成树上，表明边的两端已经在同一个连通块中。那么存在一条更小的边连接当前边的两端，又已知当前边是最小的连接两个点的边，此处产生了矛盾，故可以证明上述结论。

发现把连通块看做一个点，代入上述结论依然成立，故可得到：一个连通块向另外一个连通块连出的最小边，一定在最小生成树上。

由于一条最小边可以消除两个连通块，那么一次最少可以消除 \(\frac{t}{2}\) 个连通块（这里的 \(t\)）是连通块个数，易得最多进行 \(\log n\)​ 次每个连通块找最小边的操作，该图可以形成一棵树。

对于一般图，每次遍历 \(m\) 条边，对于每个连通块求最近连通块即可。

复杂度为：\(O(m\log n)\)。

一般适用于点数较少，边数较多，而又可以快速求出一个点最近的不在同一个连通块内的点的情况（即可以替代遍历 \(m\) 条边，求出连通块最近连通块的做法）。

接着我们考虑怎样快速的求出一个点最近的不在同一个连通块内的点。

这里的最近是在图上的最近，且不包括出发点本身的 \(a\) 值。

下文所述的路径长度也为图上的路径长度，且不包括出发点本身的 \(a\) 值。

考场手玩一下数据发现下述规律：

首先生成一棵树。

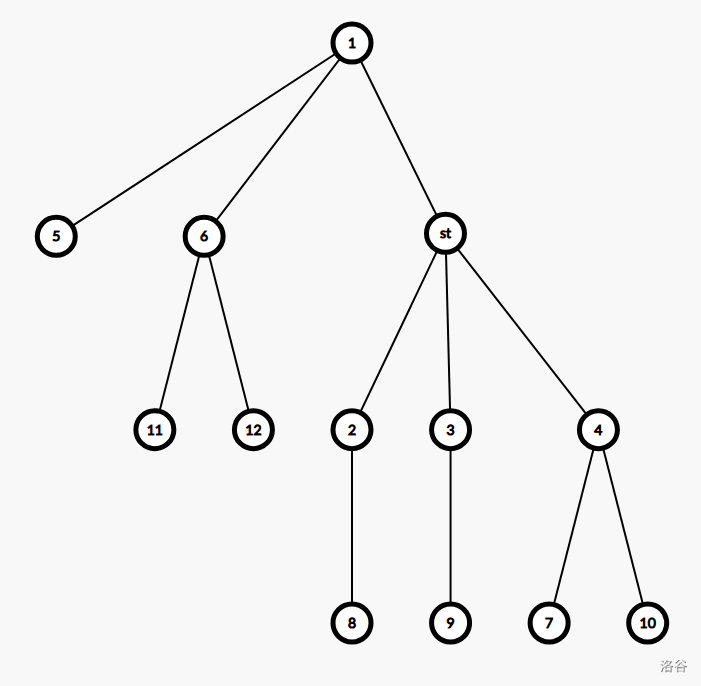
从 \(st\) 出发的最短路径为 \(st\to 12\)，长度即为下图红色线段所标的边的边权和加 \(a_{12}\)。

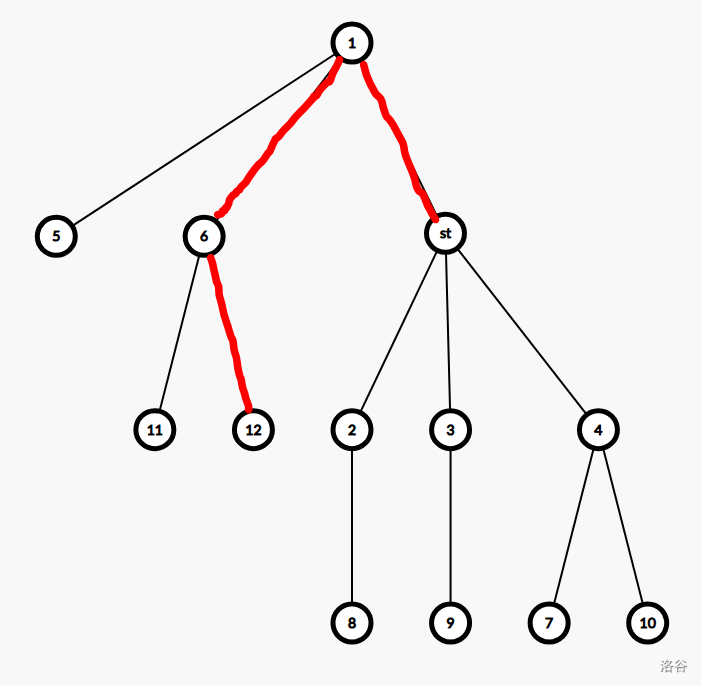
此时若某个点想要寻找最近点，若 \(st\) 在这个点最近点的路径上，那么最近点不是 \(st\) 就是 \(12\)。

证明一下，因为 \(st\) 在这个点的路径上，那么可以看做是 \(st\) 到这个点的距离加上 \(st\) 到最近的一个点的距离，所以成立。

然后你就会发现，把每一次的 \(st\) 搬到点分树上，第一次是点分树的根跑一个最近点，第二次是点分树的根的儿子跑最近点……，由于不需要经过已经求过最进点的点，所以点分树上每一层只会遍历 \(n\) 个节点。

如果需要经过已经求过最近点的点可以 \(O(1)\) 出答案。

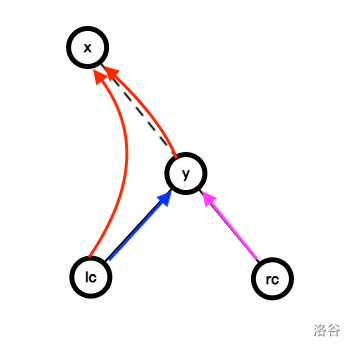
每次使用并查集判断一个点是否在同一个连通块内。如果是已经求过最近点的点（点分树上祖先），自己和其在同一个连通块那么就取其的最近点，如果不在那么就取其到其连通块内的最近点（这个肯定更优，因为第一次筛出的无限制的最近点肯定是最小的），当然也可以取其本身。

求出后直接跑 boruvka 就行。

复杂度 \(O(n\log^2n)\)，常数有一点点大。

CODE

#pragma GCC optimize(1,2,3,"Ofast","inline")
#include<bits/stdc++.h>
using namespace std;#define ll long long
#define pli pair<ll,int>
#define fi first
#define se secondconst int maxn=2e5+1;struct Edge
{int tot;int head[maxn];struct edgenode{int to,nxt,w;}edge[maxn<<1];inline void add(int x,int y,int z){tot++;edge[tot].to=y;edge[tot].nxt=head[x];edge[tot].w=z;head[x]=tot;}
}T;int n,cnt;
int f[maxn],a[maxn];ll ans;pli val[maxn],use[maxn];struct node{int u,v;ll w;}E[maxn];int rt;
int siz[maxn];
bool book[maxn],cut[maxn];
vector<int>son[maxn];char *p1,*p2,buf[100000];
#define nc() (p1==p2 && (p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++)
inline int read()
{int x=0,f=1;char ch=nc();while(ch<48||ch>57){if(ch=='-')f=-1;ch=nc();}while(ch>=48&&ch<=57)x=x*10+ch-48,ch=nc();return x*f;
}
inline void W(ll x)
{if(x<0) putchar('-'),x=-x;if(x>9) W(x/10);putchar(x%10+'0');
}
inline pli Min(pli a,pli b)
{if(a.fi<b.fi) return a;else if(a.fi==b.fi&&a.se<b.se) return a;return b;
}inline int fr(int u){return f[u]==u?u:f[u]=fr(f[u]);}
inline void dfs_siz(int u)
{book[u]=true;siz[u]=1;for(int i=T.head[u];i;i=T.edge[i].nxt){int v=T.edge[i].to;if(!book[v]&&!cut[v]) dfs_siz(v),siz[u]+=siz[v];}book[u]=false;
}
inline int dfs_rt(int u,const int tot)
{book[u]=true;int ret=u;for(int i=T.head[u];i;i=T.edge[i].nxt){int v=T.edge[i].to;if(!book[v]&&!cut[v]&&(siz[v]<<1)>tot){ret=dfs_rt(v,tot);break;}}book[u]=false;return ret;
}
inline void build(int u,int f)
{dfs_siz(u);int g=dfs_rt(u,siz[u]);cut[g]=true;son[f].emplace_back(g);for(int i=T.head[g];i;i=T.edge[i].nxt){int v=T.edge[i].to;if(!cut[v]&&!book[v]) build(v,g);}rt=g;
}inline void dfs2(int u,const int f,const int ff,ll dis)
{book[u]=true;int fu=fr(u);if(fu!=ff) val[f]=Min(val[f],{dis+a[u],u});for(int i=T.head[u];i;i=T.edge[i].nxt){int v=T.edge[i].to;if(cut[v]){if(book[v]) continue;int fv=fr(v);if(fr(use[v].se)!=ff&&fv!=ff){val[f]=Min({dis+T.edge[i].w+use[v].fi,use[v].se},val[f]);}else if(use[v].se==f&&fv!=fu) val[f]=Min({dis+T.edge[i].w+a[v],v},val[f]);else if(fv==fu) val[f]=Min({dis+T.edge[i].w+val[v].fi,val[v].se},val[f]);}else if(!book[v]&&!cut[v]) dfs2(v,f,ff,dis+T.edge[i].w);}book[u]=false;
}
inline void dfs(int g)
{cut[g]=true;dfs2(g,g,fr(g),0);if(use[g].se==0) use[g]=Min(val[g],{a[g],g});for(auto v:son[g]) dfs(v);
}
int main()
{n=read();for(int i=1;i<=n;i++) a[i]=read(),f[i]=i;for(int i=1;i<n;i++){int x,y;ll w;x=read(),y=read(),w=read();T.add(x,y,w);T.add(y,x,w);}build(1,0);memset(cut,0,sizeof(cut));E[0].w=1e18;while(cnt<n-1){dfs(rt);for(int i=1;i<=n;i++){int fv=fr(i);if(E[fv].w>val[i].fi+a[i]) E[fv]={i,val[i].se,val[i].fi+a[i]};}for(int i=1;i<=n;i++){int fv=fr(E[i].v),fu=fr(E[i].u);if(E[i].w<E[0].w&&fv!=fu){ans+=E[i].w;f[fv]=fu;cnt++;}E[i]=E[0];cut[i]=0,val[i]={1e18,1e9};}}cerr<<clock();W(ans);
}

删掉 \(IO\)，大概 3k。