CSP2024考前集训记录
2024.9.2
上午
高一学长供的题。


A题
开考5分钟想到枚举 \(a\) 后再枚举 \(d=\gcd(b,c)\) 后转化为求 \(\varphi(\frac{b+c}{d})\),直接上线性筛。
然后时间复杂度 \(O(n \sqrt n)\),瓶颈在枚举 \(b+c\) 的因数上。
于是后半个比赛全在想怎么优化,想到的包含:再套一层线性筛之类的……
结果题解是先枚举 \(d\) 再枚举 \(a\),然后复杂度就变成 \(O(n \log n \log \log n)\) 了……
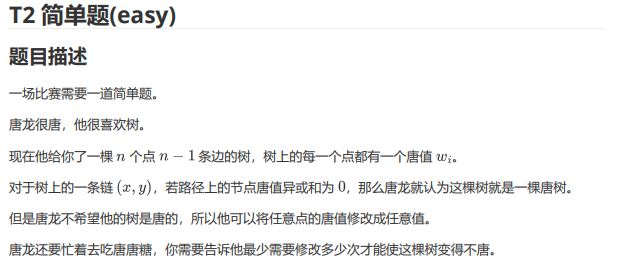

B题
想到了可以通过修改唐链上的任意一点权值为极大值,然后定根从下往上逐步处理每个子树。
然后把点权换成边权,结果忘记还有 LCA 了……
于是后面想的贪心(按子树内不同权值从小到大排序再合并)也错了。
并且合并用的启发式合并也不会。
考下3分钟补完了。


C题
刚开始没看懂题,以为一次询问只能选一次区间,于是预处理出来 \(dist(i,i+1)\) 和 \(\sum \limits^{l+k-2}_{i=l} dist(i,i+1)\),然后对于每一个询问就只需 ST表 得到区间最大值就可以了。
然后敲到一半临时发布样例解释,发现一次询问中可以选取选取多个区间,那么就得再套一个 dp。
但是多组询问是个大问题,刚开始想着从 \(1\) 开始 dp 之后差分,但是没想出来……
结果正解是整体二分套dp,不会)


D题
赛时看到概率&期望就溜了。
赛后学长只讲了前半部分(30 pts),以龙数容斥可以做到 \(O(n^3)\)。
后面就要上二项式反演了,还没学(),补完题就学。