并查集

197 图中是否存在有效路径
var father []int
func validPath(n int, edges [][]int, source int, destination int) bool {// 使用并查集算法,涉及到的操作,包括init,find, issample,joinfather = make([]int, n)for i, _ := range father { // initfather[i] = i}// insertfor _, edge := range edges {join(edge[0], edge[1])}return isSame(source, destination)
}func find(u int) int {if u == father[u] { // 只有根节点的父节点等于自己return u}res := find(father[u]) // res 保存的是多次递归之后最终的根father[u] = res // u是查询的节点,father[u] 含义是u的父节点,father[u] = res,代表将u的父节点指向根,这里操作就是路由压缩return res
}func join(u, v int) {// 先拿到u,v的根节点,不能直接对比find(u) == find(v), 因为下面还有赋值操作u = find(u)v = find(v)if u == v {return}father[u] = v
}func isSame(u, v int) bool {if find(u) == find(v) {return true}return false
}
684 冗余连接
var father []int
var res []int
func findRedundantConnection(edges [][]int) []int {// 考察并查集知识,什么叫做冗余连接呢?就是并查集中出现的路径压缩,2->1, 3->1, 3->2==>2的根是1,3的根也是1,已经再同一集合, 这就是冗余连接// 所以本题思路就是join过程如果出现了已经在同一个集合中,那么此时再插入这条边,就会出现环// initres = []int{}father = make([]int, len(edges))for i, _ := range father{father[i] = i}for _, edge := range edges {join(edge[0], edge[1])}return res
}func find(u int) int {if u == father[u] {return u}r := find(father[u])father[u] = rreturn r
}func join(u ,v int ){ // 加入u->v 这条边fu := find(u-1)fv := find(v-1)if fu == fv { // 已经在集合中res = []int{u, v}return}father[fu] = fv
}
冗余连接II
var father []int
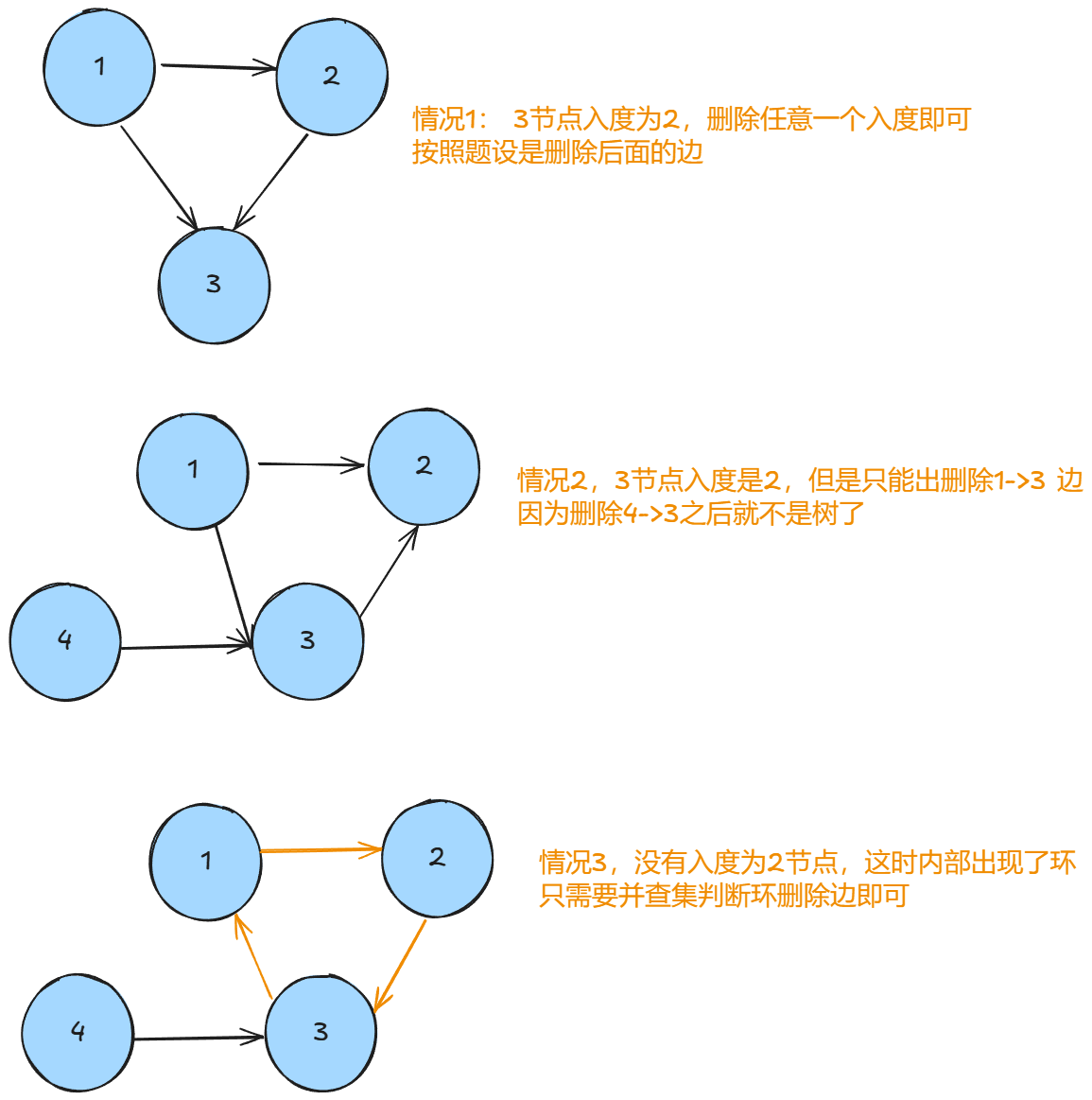
func findRedundantDirectedConnection(edges [][]int) []int {// 需要针对两种大情况,三种小情况分别处理,两大分别是是否出现节点入度为2// 如果没有入度2节点,说明出现了环,并查集删除边即可// 如果出现入度2节点,1,两条边都可以删除,那么就删除后出现的边// 2, 只有一条边能够保持删除后还是树,那就删除此边var nodeCount = make(map[int][][]int, len(edges))var node [][]int // 保存可能出现的入度2的两条边, 长度只能是0 或者 2father = make([]int, len(edges))for i ,_ := range edges{father[i] = i}// 判断是否有入度2的节点for _, edge := range edges {nodeCount[edge[1]] = append(nodeCount[edge[1]], edge)if len(nodeCount[edge[1]]) == 2{node = nodeCount[edge[1]]}}if len(node) == 0 { // 出现了环,没有入度为2的节点for _, edge := range edges {if same(edge[0], edge[1]) { // 出现了同时在集合中,这时这条要加入的边就是成环的边return edge}else {join(edge[0], edge[1])}}}else { // 出现入度为2节点// 判断一下删除之后是否还能够成树,node是顺序加入的两条边,所以遍历要倒叙,优先删除的是后面插入的边if checkTreeAfterRemove(edges, node[1]) {return node[1]}return node[0]}return []int{}
}func find(u int) int {if u == father[u] {return u}r := find(father[u])father[u] = find(father[u])return r
}func join(u, v int) {fu := find(u-1)fv := find(v-1)if fu == fv{return}father[fv] = fu
}func same(u,v int )bool {if find(u-1) == find(v-1){return true}return false
}func checkTreeAfterRemove(edges [][]int, remove []int)bool {// 思考一下原理,如果对于只能删除一条边的情况,错删除会导致出现一个单独节点,一个环,所以原理就是判断不加入这条边是否有环for _, edge := range edges {if edge[0] == remove[0] && edge[1] == remove[1] {continue}if same(edge[0], edge[1]) { // 出现了同时在集合中,这时这条要加入的边就是成环的边return false // 出现了环就是图,不是树了}else {join(edge[0], edge[1])}}return true
}