Codeforces Round 942 (Div. 1) VP 记录
我没实力打 Div1 /kk
事实上我唯一 rated 的那场 Div1 切三题是不是运气好啊 /kk /kk
A
考虑 \(k = 0\) 的时候怎么做。设最小值为 \(x\),答案显然是 \(\sum [a_i = x \vee a_i = x + 1] a_i\)。
都与最小值相关了,都最小值最大了,直接二分答案一下就行了。
唐诗 fact:你怎么知道我二分上界写 1e18 炸了调了 15min.
唐诗 fact2:←也一样开 1e18 炸了。
B1
←:推式子三行的事情
我:懒得推柿子,注意到 \(a\) 是 \(b\) 的倍数,\(n \ln n\) 暴力枚举 \(a\) 和 \(b\) 然后暴力 check 即可。
B2
←:你还能暴力吗
我:暴力不了,我开摆吧。
←:\(q\) 怎么去掉啊,带着 \(q\) 做不了啊?
我:(开 C 题
于是到最后两个人都没做出 B2。好久没复习数论了被数论水题薄纱了。
令 \(d = \gcd(a, b), a = pd, b = qd\)。
条件改为 \((pd + qd) \mid qd^2\)。
两边约掉 \(d\) 得 \((p + q) \mid qd\)。
因为 \(p \bot q\),所以 \((p + q) \bot q\),所以有 \((p + q) \mid d\)。
然后显然有 \(p < d, q < d\),又因为 \(a = pd\) 有 \(p^2 \le n\),同理有 \(q^2 \le m\)。
暴力枚举 \(p, q\),然后得到 \(d\) 的取值范围是 \([1, \min(\lfloor n / p\rfloor, \lfloor m / q \rfloor)]\)。
然后 \(d\) 要是 \((p + q)\) 的倍数,所以这一对 \((p, q)\) 的贡献是 \(\lfloor \min(\lfloor n / p\rfloor, \lfloor m / q \rfloor)] / (p + q) \rfloor\)。然后就做完了,时间复杂度 \(O(\sqrt {nm})\)。
C
所以这个人做出 C 了吗
那显然是没有啊!
考场上瞪出了是个等差数列不会维护。
考虑 \(1\) 的祖先 \(2, 4, 8\),尝试打表得到贡献。
然后能打出,当 \(k\) 为 \(2\) 时,\(a_1\) 对祖先的贡献是 \(1, 2, 3, 4, \dots\)。当 \(k\) 为 \(3\) 时它是 \(1, 3, 6, 10\),\(k\) 为 \(4\) 时是 \(1, 4, 10, 20\)。
这个东西是个 \(n\) 阶等差数列。
然后考虑求这个东西。经过一点观察,发现斜着看杨辉三角就是这个东西
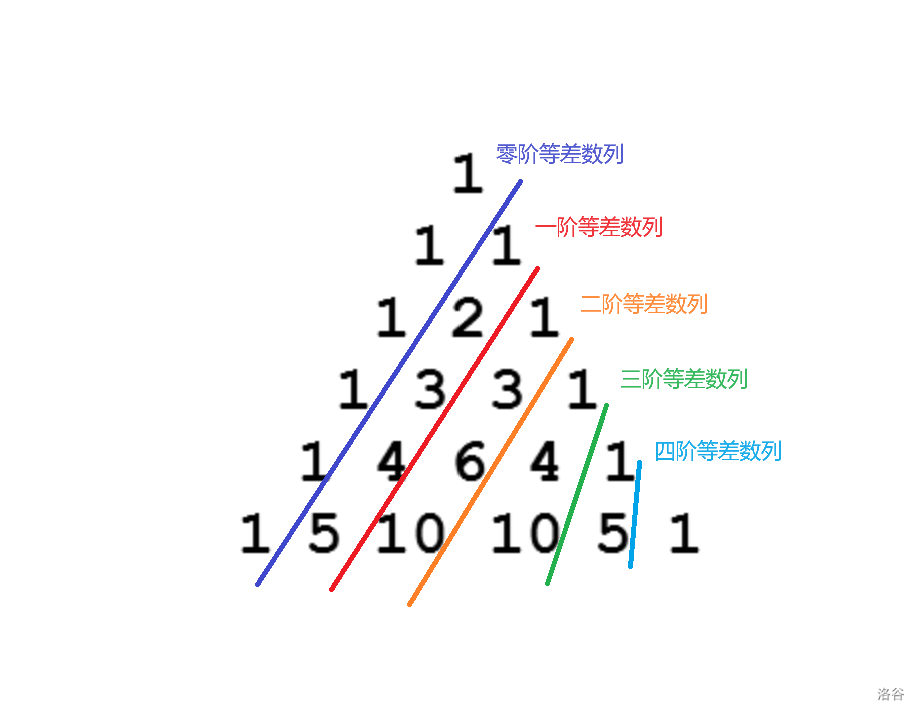
所以 \(m\) 阶等差数列 \(\{S_{m, n}\}\) 的第 \(x\) 项为 \(\binom{m + x - 1}{m}\)。
然后这题值域巨大,而我们需要的组合数是杨辉三角的一斜排,预处理 \(1\) 到 \(n\) 的逆元后递推组合数即可。
没看出是杨辉三角,如此实力,如何 NOIP。
D
我怎么觉得这个 D 这么简单呢,哪有 *2800。
但是代码难度是有的,如果 2.5h 我分配 2h 想 D 写 D 我可能写得出来(
一眼 \(i \rightarrow b_i\) 连边先转成图论题,然后是个极幻术森林。
首先,这个选集合是假的吧。假设对于每个数我们操作了 \(c_i\) 次,那么答案就是 \(\max c_i\)。
问题转化为,求 \(\max c_i\) 的最小值使得序列 \(a\) 能单调不降。
最大值最小,二分答案转为判定问题。
问题转化为,每个 \(a_i\) 能走到步数不超过 \(mid\) 的点,问能否使得 \(a\) 单调不降。
然后贪心的选,显然 \(a_i\) 应该走到能走到的点中不小于 \(a_{i - 1}\) 的点中最大的吧。
这个操作是求后继,可以树剖后用一些 heavy DS 维护得到三支 \(\log\) 做法((
然后注意到值域特别小,而且 \(a_i\) 单调不降。
那就简单了,拿个指针 \(k\) 一直往后扫,问题变成快速判定 \(k\) 和 \(a_i\) 距离是否小于给定值,也就是求两点距离。
环上是简单的,树上维护下深度也是简单的,然后简单分讨一下即可。
但是其实实现细节还是挺多的(