- 概
- 符号说明
- Adafactor
- Factored Second Moment Estimation
- No Momentum
- Out-of-Date Second Moment Estimator
- 算法
- 代码
Shazeer N. and Stern M. Adafactor: Adaptive learning rates with sublinear memory cost. ICML, 2018.
概
本文介绍了一种 memory-efficient 的优化器: Adafactor.
符号说明
- \(x\), parameters;
- \(W \subset x\), a linear transformation, $ \in \mathbb{R}^{n \times m}$
Adafactor
下面, 我们一步步介绍 Adafactor 对于 Adam 的修改.
Factored Second Moment Estimation
- 一般的 Adam 的更新流程如下:

-
一个比较重要的点是 一阶和二阶 的动量估计, 这个估计导致了 Adam 至少需要 2x 的参数的缓存.
-
假设对于 linear transformation \(W \in \mathbb{R}^{n \times m}\), 它所对应的二阶动量为: \(V \in \mathbb{R}^{n \times m}\), 作者希望将他分解成两个低秩矩阵: \(R \in \mathbb{R}^{n \times k}, S \in \mathbb{R}^{k \times m}\), 使得
\[V \approx RS. \] -
由于 \(V\) 是非负的, 所以作者更倾向于 nonnegative matrix factorization, 并利用泛化的 KL 散度—— I-divergence:
\[d(p, q) = p \log \frac{p}{q} - p + q \]作为度量.
-
作者希望 \(R, S\) 能够满足:
\[\min_{R \in \mathbb{R}^{n \times k}, S \in \mathbb{R}^{k \times m}} \quad \sum_{i=1}^n \sum_{j=1}^m d(V_{ij}, [RS]_{ij}) \\ s.t. \quad R_{ij} \ge 0, \quad S_{ij} \ge 0. \] -
特别的, 作者证明了, 在 \(k=1\) 的情况下, 一定有:
\[RS = V1_m 1_n^T V / 1_n^T V 1_m, \quad 1_{\ell} := (1, \ldots, 1) \in \mathbb{R}^{\ell} \]成立. 于是, 在这种情况下, 不失一般性的, 可以领:
\[R = V 1_m, C = 1^T V. \] -
于是, 作者给出了如下的 \(V_t\) 的更新方案:
\[G_t = \nabla f_t(W_{t-1}) \\ R_t = \beta_2 R_{t-1} + (1 - \beta_2) (G_t^2 1_m) \\ C_t = \beta_2 C_{t-1} + (1 - \beta_2) (\mathbf{1}_n^T G_t^2) \\ \hat{V}_t = (R_t C_t / 1_n^T R_t) / (1 - \beta_2^t) \\ W_t = W_{t-1} - \alpha G_t / (\sqrt{\hat{V}_t} + \epsilon). \]
No Momentum
- 为了进一步降低一阶动量的缓存, 作者直接令 \(\beta_1 = 0\), 即移除了一阶动量.
Out-of-Date Second Moment Estimator
-
作者认为, 当模型变化特别快的时候, 二阶矩的估计很容易过时:

-
如上图所示, 当我们用一个较大的 \(\beta_2\), 如果没有 warm-up (即模型缓慢更新) 阶段, 效果是特别差的.
-
为了验证这一点, 作者统计:
\[\text{RMS}(U_t) = \text{RMS}_{x \in X} (u_{xt}) = \sqrt{\text{Mean}_{x \in X} (\frac{g_{xt}^2}{\hat{v}_{xt}} )}. \]作者认为, 如果训练是稳定的, \(\text{RMS}(U_t) \approx 1\), 既然 Adam 的一个假设是:
\[\mathbb{E}[\hat{v}] = \mathbb{E}[g^2]. \]
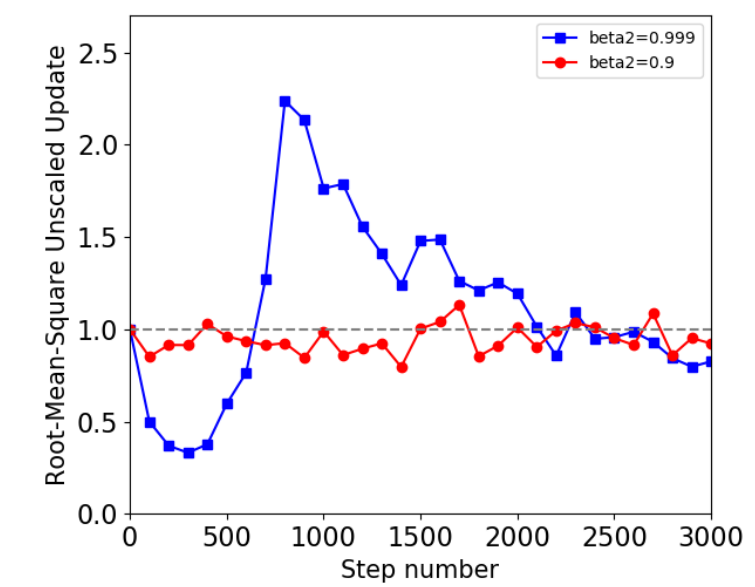
- 如上图所示, \(\beta_2\) 取得比较大的时候, 结果并不是这样的. 于是:\[U_t= G_t / \sqrt{\hat{V}_t} \\ \hat{U}_t = U_t / \max(1, RMS(U_t) / d) \\ W_t = W_{t-1} - \alpha_t \hat{U}_t. \]即 Adafactor 会手动校准.
算法
- Adafactor 对于 matrix:

-
Adafactor 对于 vector:

-
默认的参数设置:

注: \(\rho\) 是人为设置的相对步长, 这里不多赘述了.
代码
[pytorch-optimizer]