网络计划技术最早由美国杜邦公司于1957年开发的“关键路径法(CPM)”和美国海军在1958年发明的“计划评审技术(PERT)”推动。网络计划技术(Network Planning Techniques)是一种用于项目管理和调度的科学方法,其核心思想是通过构建网络图来描述项目中各个任务之间的逻辑关系,进而分析和优化项目的时间、成本等资源分配。该技术自20世纪50年代诞生以来,经历了不断的发展和应用创新,已成为现代项目管理中不可或缺的工具。
| 网路计划图 | 时间参数 |
|---|---|
 |
 |
一、网络计划技术
网络计划技术(Network Planning Techniques)是一种用于项目管理和调度的科学方法,其核心思想是通过构建网络图来描述项目中各个任务之间的逻辑关系,进而分析和优化项目的时间、成本等资源分配。该技术自20世纪50年代诞生以来,经历了不断的发展和应用创新,已成为现代项目管理中不可或缺的工具。
关键路径法(CPM,Critical Path Method):CPM最早用于化工工业项目管理,旨在帮助项目管理者确定项目中最重要、最关键的任务,分析出这些任务的最短完成时间及其对整个项目的影响。关键路径法通过计算各个任务的最早开始时间、最迟完成时间等参数,识别出对项目工期至关重要的“关键路径”。
计划评审技术(PERT,Program Evaluation and Review Technique):PERT最初被用于“北极星”导弹项目,与CPM不同的是,PERT主要用于解决不确定性较高的项目,它通过概率统计的方法来估算任务的完成时间,并分析出项目的总完成时间及其可靠性。
1.1 网络计划图概述
随着计算机技术的发展,网络计划技术的计算和应用得到了极大简化,使其不仅仅局限于大型项目,而逐渐扩展到各行各业。70年代之后,项目管理软件的普及进一步推动了网络计划技术的标准化和应用扩展,诸如Microsoft Project等工具让项目管理者能够更加便捷地构建网络图并进行调度分析。
- 作业明细表
构建网络计划图需要从项目的作业或工序明细表入手。作业明细表通常列出所有的项目活动(如任务A、B、C等),并标明每项活动的持续时间和前置工序(紧前工序)。紧前工序指的是在当前活动开始之前必须完成的活动。这个信息是创建网络图的基础,明确了项目中各任务的相互依赖关系。例如,活动A可能是活动C的紧前工序,意味着C不能开始,直到A完成。
| 作业明细表 | 网络计划图 |
|---|---|
 |
 |
-
网络计划图的绘制
在建立网络计划图时,每个活动通常用节点或箭头表示,节点代表活动,箭头表示活动之间的依赖关系。活动的顺序从无前置任务的起始活动开始,逐步展开,直到最终活动完成为止。网络计划图通常有两种主要形式:箭线图法(Activity on Arrow,AOA)和节点图法(Activity on Node,AON)。在AOA中,活动由箭线表示,节点代表事件;而在AON中,活动用节点表示,箭线代表活动之间的依赖关系。 -
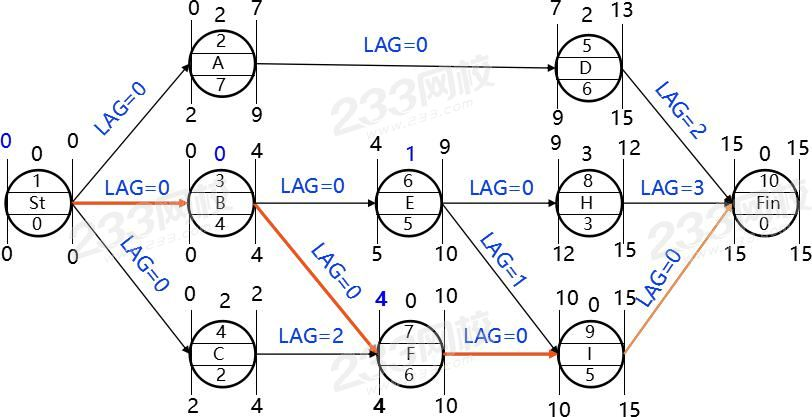
时间参数的计算
| 时间参数计算示意图 | 时间参数 |
|---|---|
 |
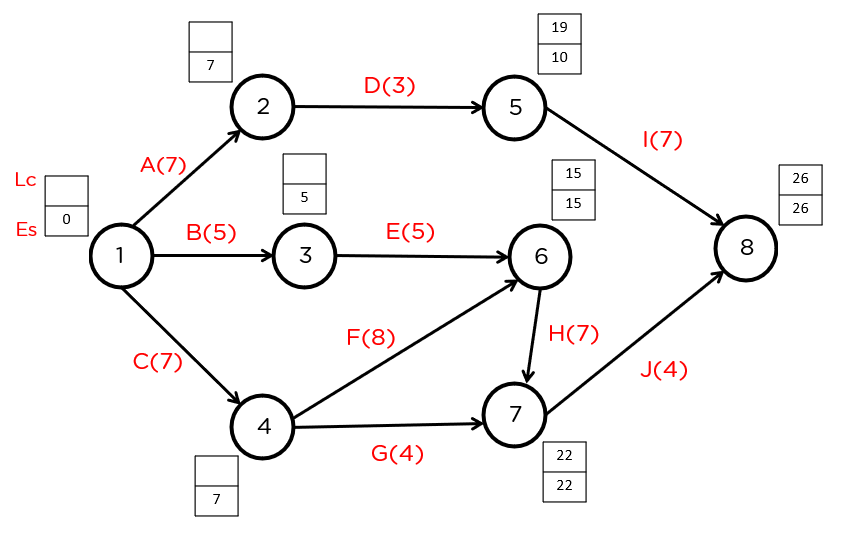 |
关键路径法通过计算项目活动的以下时间参数来分析项目的进度计划:
最早开始时间(ES):指某一任务可以在不延误前置任务的情况下,最早可以开始的时间。\[ES(i) = \max\{EF(j) \mid j \in \text{前置任务}\} \]如果没有前置任务,则其ES为0。
最早完成时间(EF):指任务在其最早开始后,最早能够完成的时间。\[EF(i) = ES(i) + \text{任务持续时间} \]这是在理想情况下任务能够完成的最早时间。
最迟完成时间(LF):指任务在不延误整个项目的情况下,最晚必须完成的时间。\[LF(i) = \min\{LS(j) \mid j \in \text{后续任务}\} \]对于没有后续任务的任务,LF等于项目的最晚完成时间。
最迟开始时间(LS):指任务最晚可以开始的时间,而不导致项目延误。\[LS(i) = LF(i) - \text{任务持续时间} \]总时差(TF):表示任务可以延迟的最大时间量,而不会影响项目的最终完成时间。
\[TF(i) = LF(i) - EF(i)\quad 或 TF(i) = LS(i) - ES(i) \]若TF为0,说明该任务是关键任务,任何延误都会导致整个项目延迟。
自由时差(FF):指在不影响后续任务最早开始的前提下,任务可以延迟的时间。\[FF(i) = \min\{ES(j) \mid j \in \text{后续任务}\} - EF(i) \]如果FF为0,意味着任务的延迟会直接影响后续任务的开始。
关键路径是项目中持续时间最长的任务链,决定了整个项目的最早完成时间。该路径上的任务称为关键任务(Critical Activities),这些任务没有任何时间余地,即它们的总时差(TF)为0,任何延误都会直接导致项目延期。关键路径的长度等于关键任务的持续时间之和,也是项目的最短完成时间。关键路径可能不止一条,但所有关键路径上的任务都必须特别关注和控制,以确保项目顺利进行。通过关键路径法和这些时间参数的计算,项目经理可以清晰地知道哪些任务需要优先处理,哪些任务有时间余地,从而更好地管理时间和资源。
1.2 网络计划技术的应用
网络计划技术由于其优越的任务调度和资源优化能力,已经在全球范围内广泛应用,涉及到以下主要领域:
建筑工程管理:在建筑项目中,任务的数量多、工期长,且各任务之间存在复杂的依赖关系。通过网络计划技术,可以有效地规划项目的关键路径,识别影响项目进度的瓶颈环节,确保工程按计划推进。
航空航天与国防工业:PERT技术尤其适用于复杂度高、不确定性大的大型国防项目,如导弹开发、卫星发射等。该技术通过引入概率评估任务的工期,帮助项目管理者更好地预测项目的总工期。
信息技术与软件开发:在现代软件开发中,项目的并行性和复杂性越来越高。使用网络计划技术可以理清各个模块之间的依赖关系,确保项目在有限的时间内按计划交付。
制造业生产调度:在制造业的流水线生产中,任务的顺序和资源的配置至关重要。通过网络计划技术,生产企业可以更好地安排各工序之间的衔接,减少停工时间,提高生产效率。
科研与研发项目管理:研发项目由于存在较大的不确定性,PERT的应用尤为广泛。通过对各项任务进行评估,项目管理者能够制定合理的研发计划,减少项目风险。
1.3 网络计划技术的分类
网络计划技术按照其不同的数学模型和应用背景,大致可以分为以下几类:
关键路径法(CPM):关键路径法主要用于任务工期确定、任务之间关系明确的项目中。通过识别关键路径,CPM能够为管理者提供项目进度控制的依据。
计划评审技术(PERT):PERT适用于任务工期不确定、需要对时间进行概率估算的项目。通过估算乐观时间、悲观时间和最可能时间,PERT能够给出项目的工期预估及其概率分布。
前导图法(PDM,Precedence Diagramming Method):前导图法是关键路径法的扩展版本,通过允许任务之间有更多的关系(如开始-开始、结束-结束等),它在复杂项目中具有更大的灵活性和表达力。
时标网络图(Time-scaled Network Diagram):时标网络图通过将网络图的横轴与时间对齐,清晰直观地展示任务的时间安排,适用于需要进行时间管理和资源分配的项目。
资源约束项目调度法(RCPSP,Resource-Constrained Project Scheduling Problem):RCPSP模型是在关键路径法基础上加入资源限制条件,适用于需要对资源进行精细调度的项目,如多项目、多任务的制造业环境。
二、网络时间参数和关键路线的Python计算
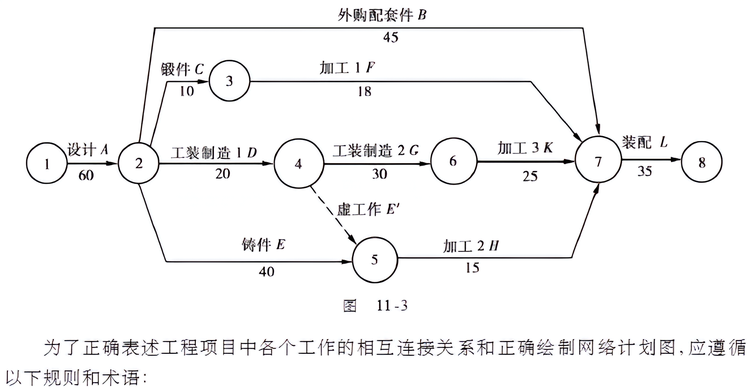
2.1 紧后作业的工序明细表
就下面工序明细表计算各工序的6个时间参数,并给出关键路线。
| 工序 | 产品及工艺设计 | 外购配套件 | 下料、锻件 | 工装制造1 | 木模、铸件 | 机械加工1 | 工装制造2 | 机械加工2 | 机械加工3 | 工装制造3 | 装配调试 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 工序代号 | a | b | c | d | e | f | g | h | i | j | k |
| 所需时间 | 60 | 45 | 10 | 20 | 40 | 18 | 30 | 15 | 25 | 25 | 35 |
| 紧后工序 | b, c, d, e | j | f | g, h | h | j | i | j | j | k | - |

import networkx as nx
import pandas as pd# 定义工序及其依赖关系、工序时间
processes = {'a': {'time': 60, 'successors': ['b', 'c', 'd', 'e']},'b': {'time': 45, 'successors': ['j']},'c': {'time': 10, 'successors': ['f']},'d': {'time': 20, 'successors': ['g', 'h']},'e': {'time': 40, 'successors': ['h']},'f': {'time': 18, 'successors': ['j']},'g': {'time': 30, 'successors': ['i']},'h': {'time': 15, 'successors': ['j']},'i': {'time': 25, 'successors': ['j']},'j': {'time': 25, 'successors': ['k']},'k': {'time': 35, 'successors': []}
}# 创建一个有向图
G = nx.DiGraph()# 将工序和时间加入图中
for process, details in processes.items():for successor in details['successors']:G.add_edge(process, successor, weight=details['time'])# 计算关键路径法的6个时间参数
def cpm_schedule(graph):# 计算最早开始时间和最早完成时间es = {node: 0 for node in graph.nodes()} # 最早开始时间ef = {node: 0 for node in graph.nodes()} # 最早完成时间for node in nx.topological_sort(graph):es[node] = max([ef[pred] for pred in graph.predecessors(node)] + [0])ef[node] = es[node] + processes[node]['time']# 计算最迟完成时间和最迟开始时间lf = {node: float('inf') for node in graph.nodes()}ls = {node: float('inf') for node in graph.nodes()}# 获取最后一个工序的最早完成时间作为项目的结束时间project_duration = max(ef.values())end_nodes = [node for node in graph.nodes() if not list(graph.successors(node))]for node in end_nodes:lf[node] = project_durationls[node] = lf[node] - processes[node]['time']for node in reversed(list(nx.topological_sort(graph))):for succ in graph.successors(node):lf[node] = min(lf[node], ls[succ])ls[node] = lf[node] - processes[node]['time']return es, ef, ls, lf# 调用关键路径法计算时间参数
es, ef, ls, lf = cpm_schedule(G)# 计算总时差和自由时差
def calculate_tf_ff(graph, es, ef, ls, lf):# 计算总时差 (TF)tf = {node: lf[node] - ef[node] for node in graph.nodes()} # 总时差# 计算自由时差 (FF)ff = {}for node in graph.nodes():if list(graph.successors(node)):ff[node] = min([es[succ] - ef[node] for succ in graph.successors(node)])else:ff[node] = 0 # 对于没有后继工序,自由时差为0return tf, ff# 调用计算总时差和自由时差
tf, ff = calculate_tf_ff(G, es, ef, ls, lf)# 将工序时间提取出来
process_times = {node: details['time'] for node, details in processes.items()}# 将结果放入数据框中,并添加一列工序time
df = pd.DataFrame({'工序': list(es.keys()),'工序time': [process_times[node] for node in es.keys()],'ES(最早开始时间)': list(es.values()),'EF(最早完成时间)': list(ef.values()),'LS(最迟开始时间)': list(ls.values()),'LF(最迟完成时间)': list(lf.values()),'TF(总时差)': list(tf.values()),'FF(自由时差)': list(ff.values())
})# 按工序字母顺序排序
df = df.sort_values(by='工序')# 输出数据框
print(df)# 计算关键路径
critical_path = nx.dag_longest_path(G, weight='weight')
print("\n关键路径:", " -> ".join(critical_path))
关键路径: a -> d -> g -> i -> j -> k
| 工序 | time | ES | EF | LS | LF | TF | FF |
|---|---|---|---|---|---|---|---|
| a | 60 | 0 | 60 | 0 | 60 | 0 | 0 |
| b | 45 | 60 | 105 | 90 | 135 | 30 | 30 |
| c | 10 | 60 | 70 | 107 | 117 | 47 | 0 |
| d | 20 | 60 | 80 | 60 | 80 | 0 | 0 |
| e | 40 | 60 | 100 | 80 | 120 | 20 | 0 |
| f | 18 | 70 | 88 | 117 | 135 | 47 | 47 |
| g | 30 | 80 | 110 | 80 | 110 | 0 | 0 |
| h | 15 | 100 | 115 | 120 | 135 | 20 | 20 |
| i | 25 | 110 | 135 | 110 | 135 | 0 | 0 |
| j | 25 | 135 | 160 | 135 | 160 | 0 | 0 |
| k | 35 | 160 | 195 | 160 | 195 | 0 | 0 |
2.2 紧前作业的工序明细表
就下面工序明细表计算各工序的6个时间参数,并给出关键路线。
| 活动名称 | 紧前工序 | 活动时间 | 活动名称 | 紧前工序 | 活动时间 |
|---|---|---|---|---|---|
| A | - | 4 | F | C, D | 9 |
| B | - | 6 | G | C, D | 7 |
| C | A | 6 | H | E, F | 4 |
| D | B | 7 | I | G | 8 |
| E | B | 5 |

import networkx as nx
import pandas as pd# 定义活动及其依赖关系、活动时间
tasks = {'A': {'time': 4, 'predecessors': []}, # 没有紧前工序'B': {'time': 6, 'predecessors': []}, # 没有紧前工序'C': {'time': 6, 'predecessors': ['A']}, # A 是 C 的紧前工序'D': {'time': 7, 'predecessors': ['B']}, # B 是 D 的紧前工序'E': {'time': 5, 'predecessors': ['B']}, # B 是 E 的紧前工序'F': {'time': 9, 'predecessors': ['C', 'D']}, # C 和 D 是 F 的紧前工序'G': {'time': 7, 'predecessors': ['C', 'D']}, # C 和 D 是 G 的紧前工序'H': {'time': 4, 'predecessors': ['E', 'F']}, # E 和 F 是 H 的紧前工序'I': {'time': 8, 'predecessors': ['G']} # G 是 I 的紧前工序
}# 创建一个有向图
G = nx.DiGraph()# 将任务和紧前工序加入图中
for task, details in tasks.items():for pred in details['predecessors']:G.add_edge(pred, task, weight=tasks[pred]['time'])# 计算关键路径法的6个时间参数
def cpm_schedule(graph):# 计算最早开始时间和最早完成时间es = {node: 0 for node in graph.nodes()} # 最早开始时间ef = {node: 0 for node in graph.nodes()} # 最早完成时间for node in nx.topological_sort(graph):es[node] = max([ef[pred] for pred in graph.predecessors(node)] + [0])ef[node] = es[node] + tasks[node]['time']# 计算最迟完成时间和最迟开始时间lf = {node: float('inf') for node in graph.nodes()}ls = {node: float('inf') for node in graph.nodes()}# 获取最后一个工序的最早完成时间作为项目的结束时间project_duration = max(ef.values())end_nodes = [node for node in graph.nodes() if not list(graph.successors(node))]for node in end_nodes:lf[node] = project_durationls[node] = lf[node] - tasks[node]['time']for node in reversed(list(nx.topological_sort(graph))):for succ in graph.successors(node):lf[node] = min(lf[node], ls[succ])ls[node] = lf[node] - tasks[node]['time']return es, ef, ls, lf, project_duration# 调用关键路径法计算时间参数
es, ef, ls, lf, project_duration = cpm_schedule(G)# 计算总时差和自由时差
def calculate_tf_ff(graph, es, ef, ls, lf):# 计算总时差 (TF)tf = {node: lf[node] - ef[node] for node in graph.nodes()} # 总时差# 计算自由时差 (FF)ff = {}for node in graph.nodes():if list(graph.successors(node)):ff[node] = min([es[succ] - ef[node] for succ in graph.successors(node)])else:ff[node] = 0 # 对于没有后继工序,自由时差为0return tf, ff# 调用计算总时差和自由时差
tf, ff = calculate_tf_ff(G, es, ef, ls, lf)# 将工序时间提取出来
task_times = {node: details['time'] for node, details in tasks.items()}# 将结果放入数据框中,并添加一列任务time
df = pd.DataFrame({'任务': list(es.keys()),'任务时间': [task_times[node] for node in es.keys()],'ES(最早开始时间)': list(es.values()),'EF(最早完成时间)': list(ef.values()),'LS(最迟开始时间)': list(ls.values()),'LF(最迟完成时间)': list(lf.values()),'TF(总时差)': list(tf.values()),'FF(自由时差)': list(ff.values())
})# 按任务字母顺序排序
df = df.sort_values(by='任务')# 输出数据框
print(df)# 手动计算关键路径
def find_critical_path(graph, tf):critical_path = []start_nodes = [node for node in graph.nodes() if not list(graph.predecessors(node))]for start in start_nodes:path = [start]current = start# 一直沿着 TF == 0 的任务前进while list(graph.successors(current)):successors = [succ for succ in graph.successors(current) if tf[succ] == 0]if successors:next_task = successors[0] # 如果有多个符合条件的后继任务,选择第一个path.append(next_task)current = next_taskelse:breakcritical_path.append(path)# 找到最长的路径作为关键路径critical_path = max(critical_path, key=len)return critical_path# 查找关键路径
critical_path = find_critical_path(G, tf)
print("\n关键路径:", " -> ".join(critical_path))
print("关键路径长度:", project_duration)
关键路径: B -> D -> G -> I
关键路径长度: 28
| 任务 | 任务时间 | ES | EF | LS | LF | TF | FF |
|---|---|---|---|---|---|---|---|
| A | 4 | 0 | 4 | 3 | 7 | 3 | 0 |
| B | 6 | 0 | 6 | 0 | 6 | 0 | 0 |
| C | 6 | 4 | 10 | 7 | 13 | 3 | 3 |
| D | 7 | 6 | 13 | 6 | 13 | 0 | 0 |
| E | 5 | 6 | 11 | 19 | 24 | 13 | 11 |
| F | 9 | 13 | 22 | 15 | 24 | 2 | 0 |
| G | 7 | 13 | 20 | 13 | 20 | 0 | 0 |
| H | 4 | 22 | 26 | 24 | 28 | 2 | 0 |
| I | 8 | 20 | 28 | 20 | 28 | 0 | 0 |
总结
网络计划技术通过图形化的方法,将复杂项目中的任务及其相互关系清晰地表达出来,帮助项目管理者识别出项目的关键路径,分析各任务的时间需求与资源配置,并做出科学的项目调度决策。其主要目标是通过优化任务调度来实现项目的按时、按质、按量完成。从CPM、PERT的初步发展,到如今更加精细化的PDM和RCPSP,网络计划技术已经成为现代项目管理中的核心工具之一。随着项目复杂度的提升,未来的网络计划技术可能会进一步与大数据、人工智能等技术结合,实现更加精准的项目调度与优化。网络计划技术不仅仅是传统项目管理中的方法论,它已经深刻融入到各行业的项目实践中。通过不断发展和创新,这一技术将在更广泛的领域发挥其独特的价值,帮助各类组织更好地应对复杂项目带来的挑战。

参考资料
- 深度学习网络计算时间 echo 计算网络时间参数例题
- 双代号网络图计算