名字:
\(DL\),\(Dancing\space Link\),舞蹈链,是由\(Donald\space Knuth\)提出的数据结构,用来优化 \(X\) 算法,所以叫\(DLX\)
\(X\)算法详解
用于求解精确覆盖问题,精确覆盖问题的定义:给定一个由0-1组成的矩阵,是否能找到一个行的集合,使得集合中每一列都恰好包含一个1
例:
若\(A,B,C \subseteq S\)
\(A \space \cap \space B= Ø\),\(A \space \cup \space B=S\),则集合\(A,B\)是问题的一种解
\(X\)算法求解模拟:
给出矩阵\(A\)
选择第一列:
将有\(1\)的列向下延伸,若该行有\(1\),标记该行,处理\(A\)矩阵,得到\(B\)矩阵
\(S矩阵=A矩阵-B矩阵\)(删除所标记的行和列)
再选择第一列
标记
得到新矩阵,又得到一个规模较小的精确覆盖问题
发现\(A\)矩阵不是空的,也没有一列有\(1\)(无法继续操作)
回溯
不能尝试第一行,标记第二行,尝试继续拓展
同理可得
\(A_3\)中只有\(1\)行,且都是\(1\),选择这行,问题就可以解决
故,问题的解就是矩阵\(A\)中的第一行、矩阵\(A_1\)中的第\(2\)行、矩阵\(A_3\)的第一行,即矩阵\(A\)中的第\(1、4、5\)行
言归正传,DLX又是什么东西呢
介绍DL,舞蹈链

建出形如这样的交叉十字循环双向链,只对有\(1\)的连边,这张图对应着矩阵\(A\)
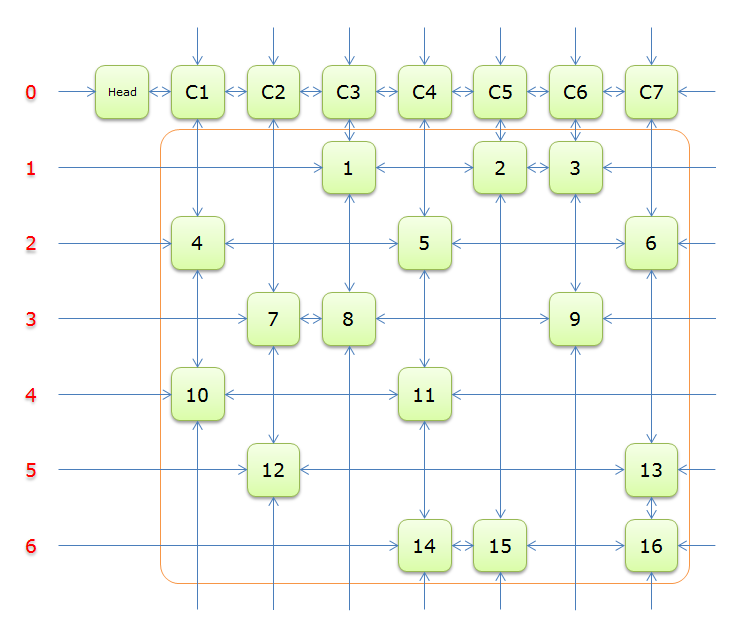
获取\(head.right\)元素,即元素\(C1\),标示元素\(C1\)为紫色
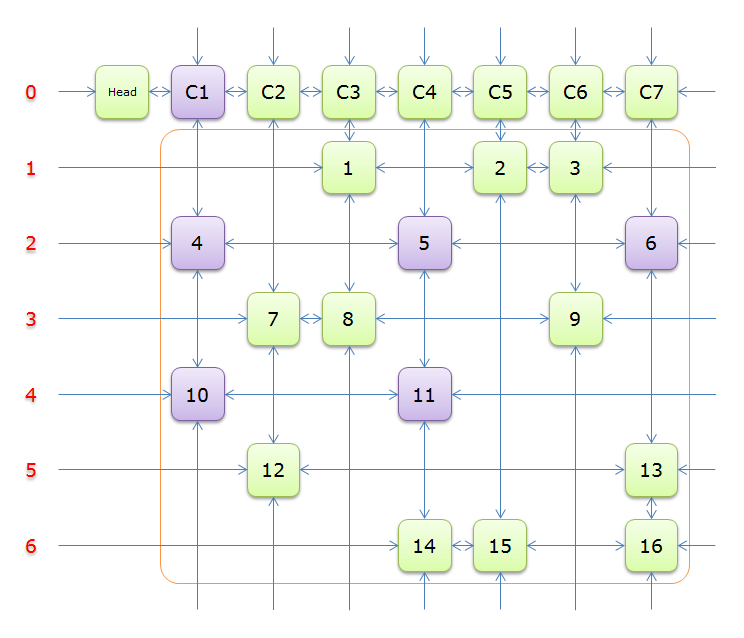
先尝试行\(2\),标示该行中其他元素\(元素5和元素6\)所在的列首元素为橙色,即元素\(C4\)和元素\(C7\)
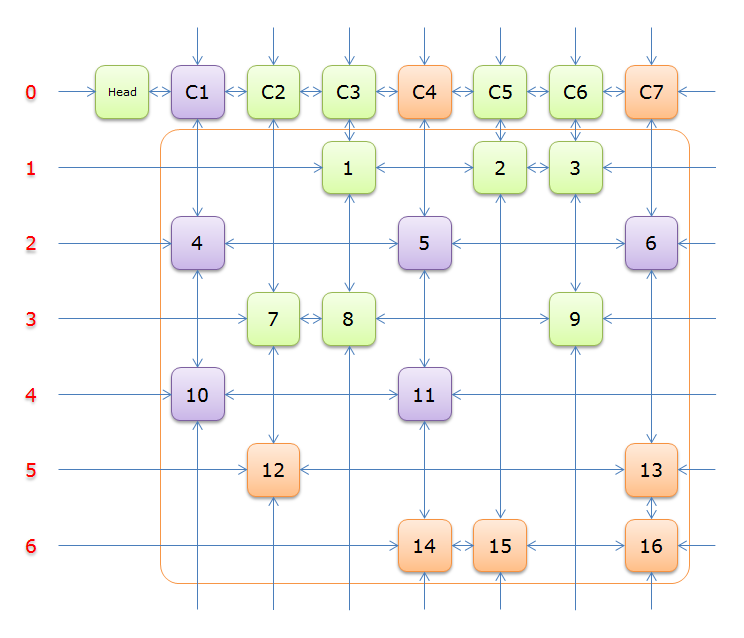
移除橙色部分和紫色部分,剩下的如图所示
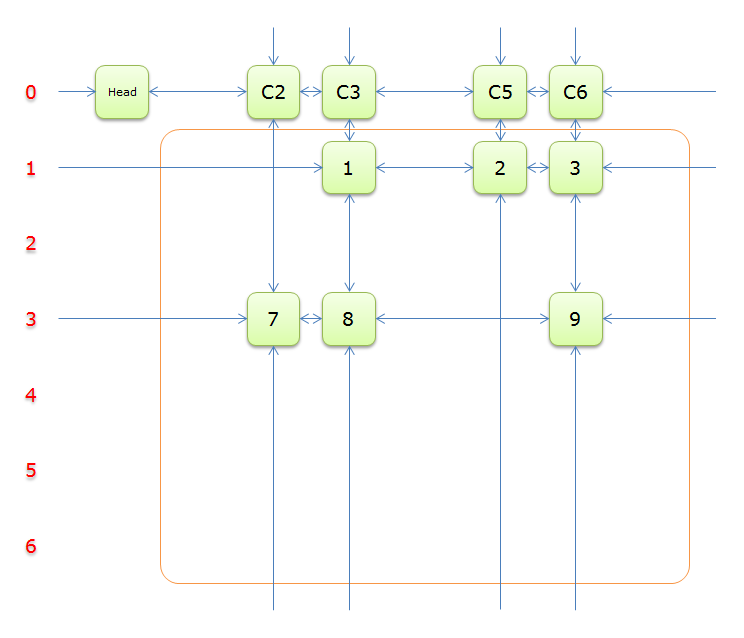
获取\(head.right\)元素,即元素\(C2\),标示元素\(C2\)为紫色
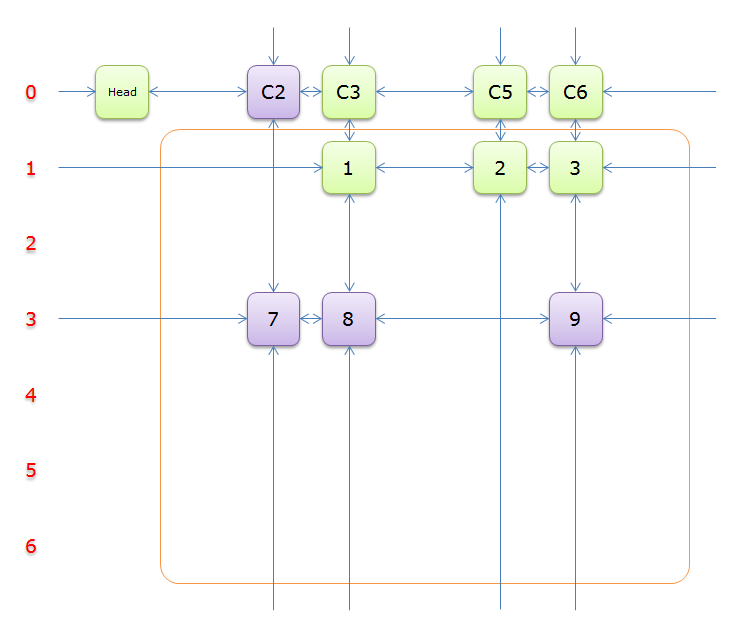
列\(C2\)只有元素\(7\)覆盖,故答案只能选择行\(3\)
选择行\(3\),同理,标示元素\(C3\)和标示元素\(C6\)为橙色
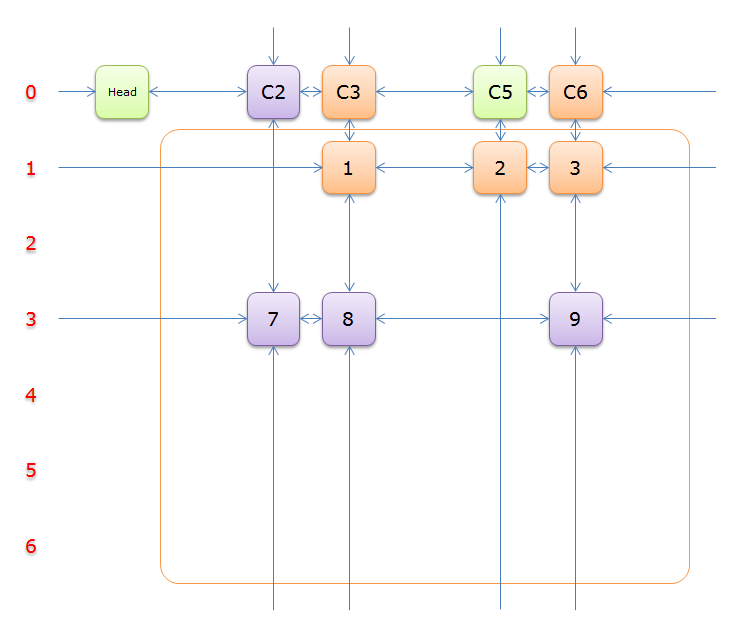
移除,得
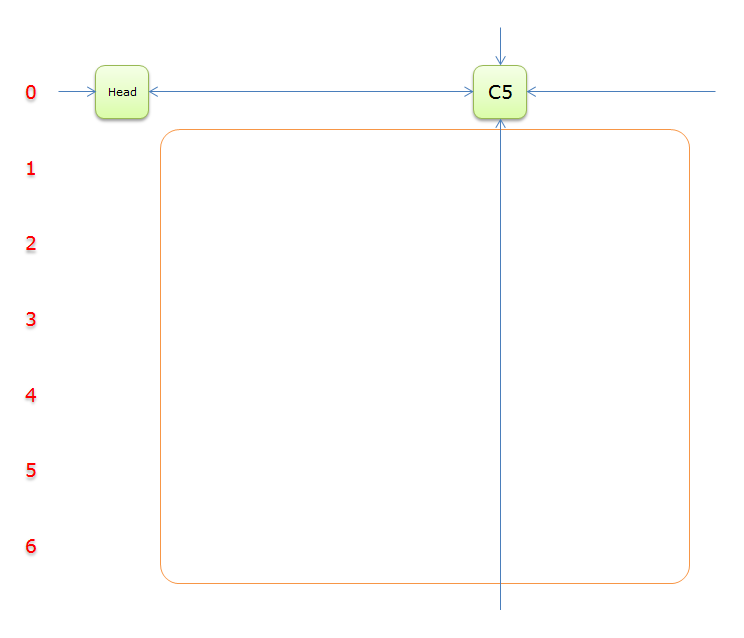
没有元素能覆盖到\(C5\),说明求解失败,回溯
回标列首元素,其顺序是标示元素的顺序反过来,即回标列首C6、回标列首C3、回标列首C2、回标列首C7、回标列首C4
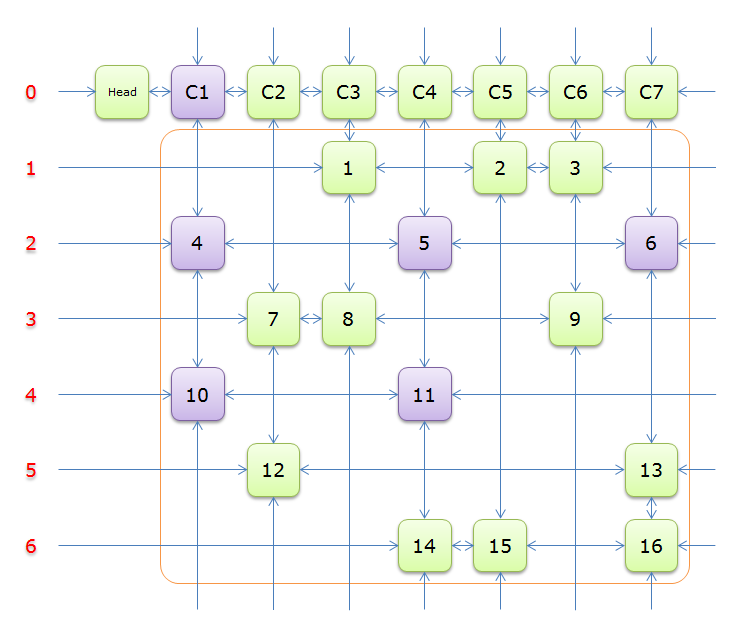
故不能选择行\(2\),尝试行\(4\),同理,标示元素\(C4\)为橙色
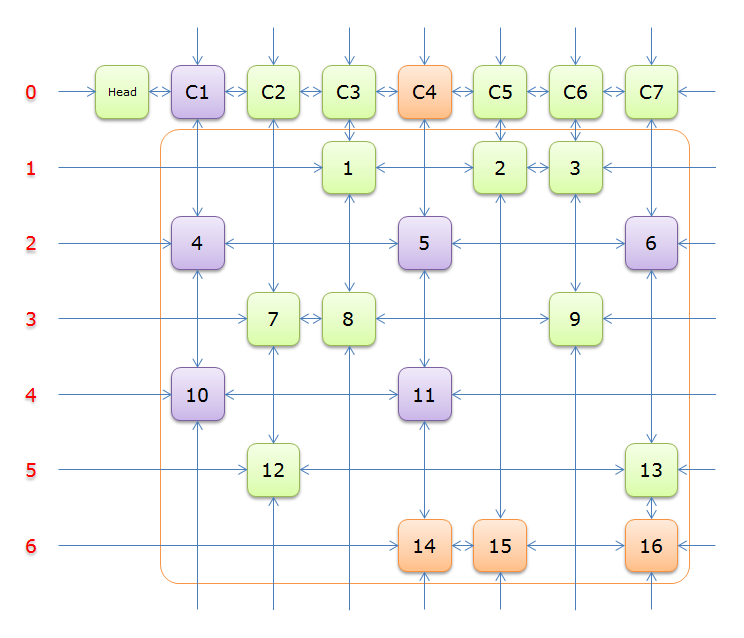
移除,得
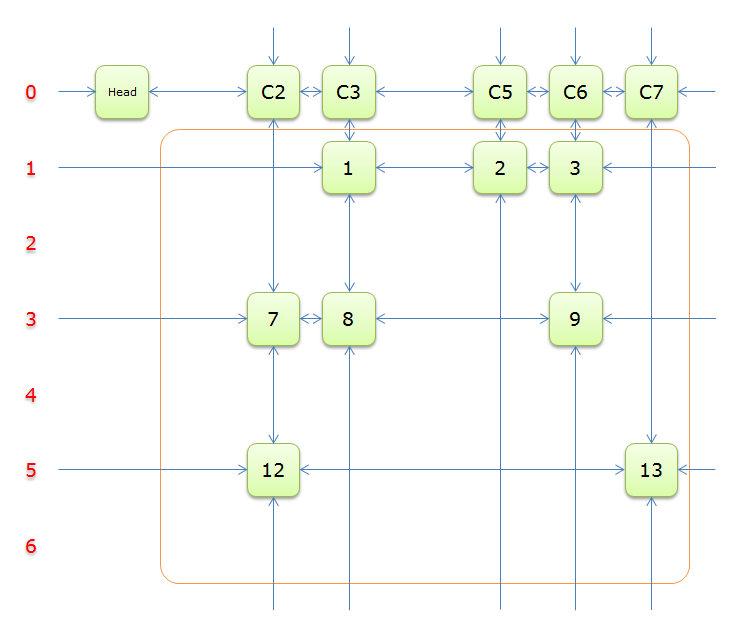
获取\(head.right\)元素,标示元素\(C2\)为紫色
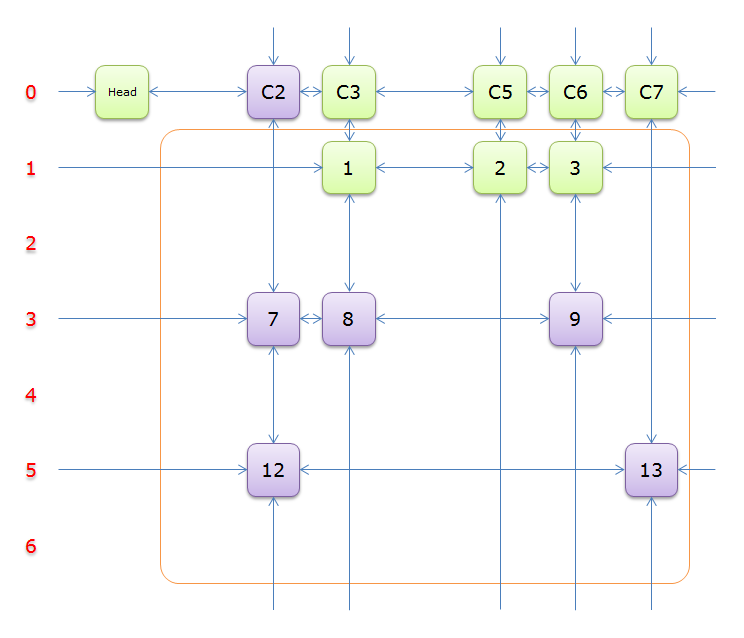
选择行\(3\),同理,标示元素\(C3\)和\(C6\)为橙色
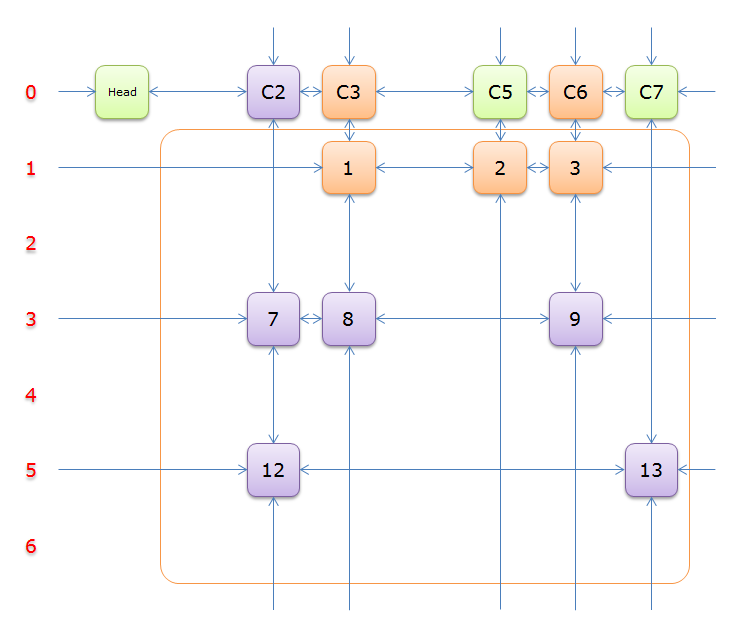
同理,得
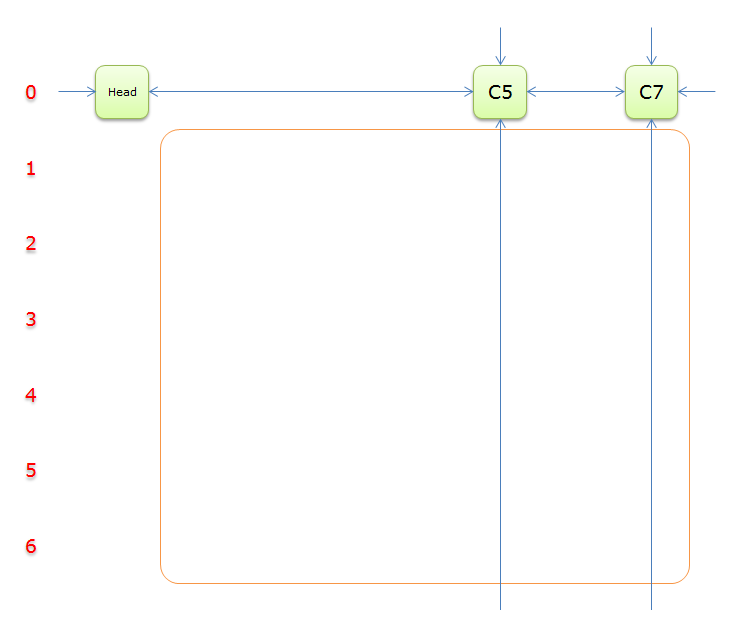
同理,回溯,回标列首C6、回标列首C3
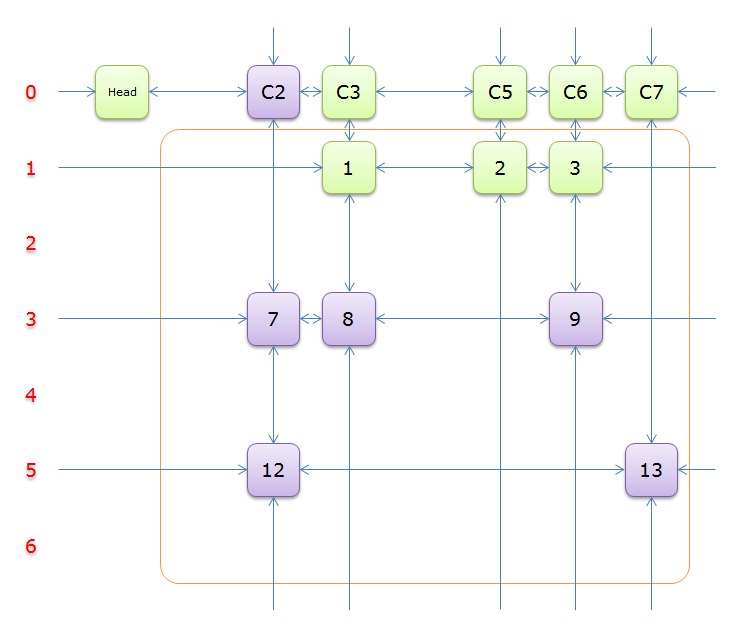
这次选择行\(5\),标示元素\(C7\)为橙色
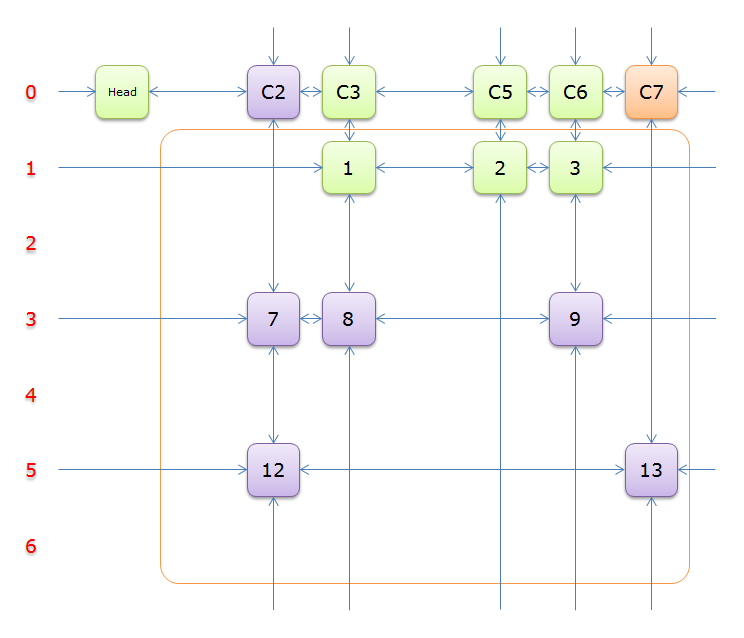
移除,得
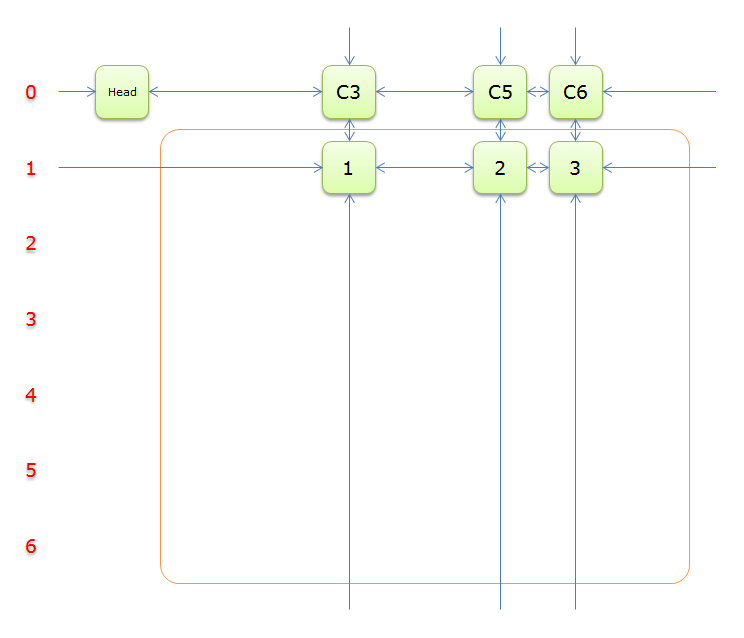
获取\(head.right\)元素,标示元素\(C3\)为紫色
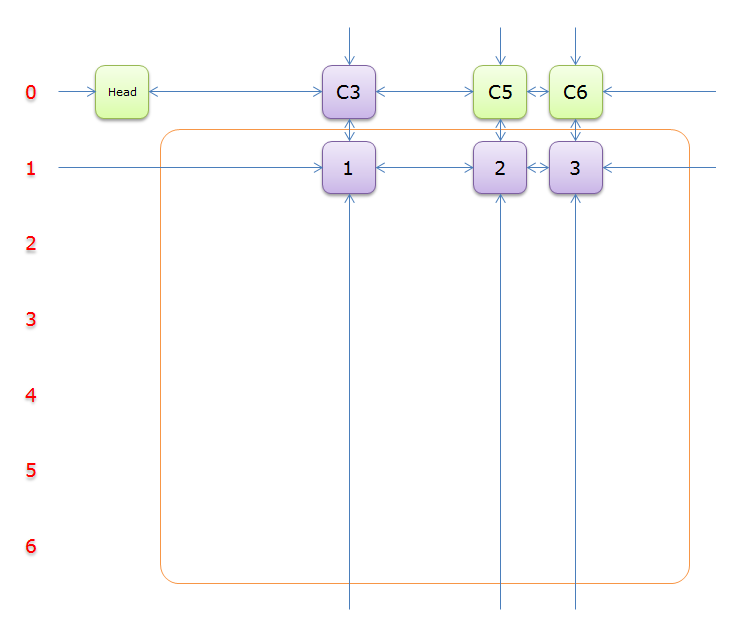
只有元素\(1\)覆盖,故答案只能选择行\(3\),同理,标示元素\(C5\)和元素\(C6\)为橙色
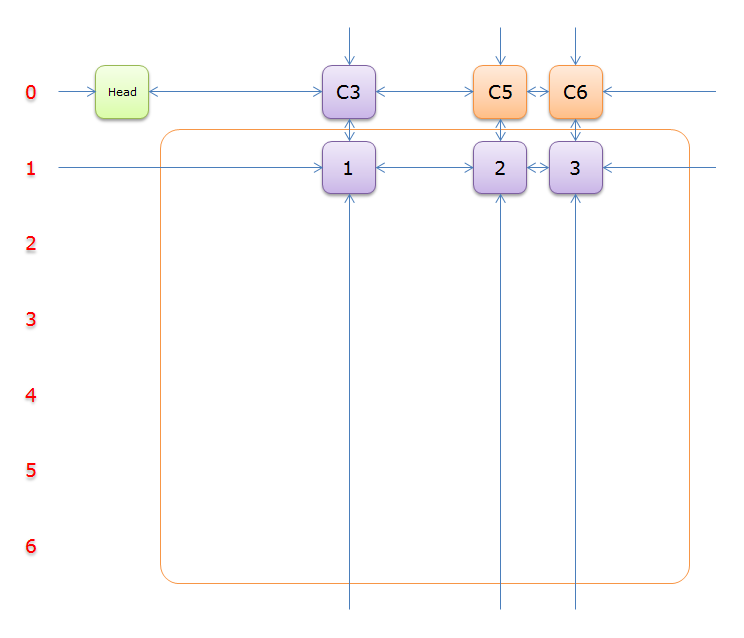
移除,得
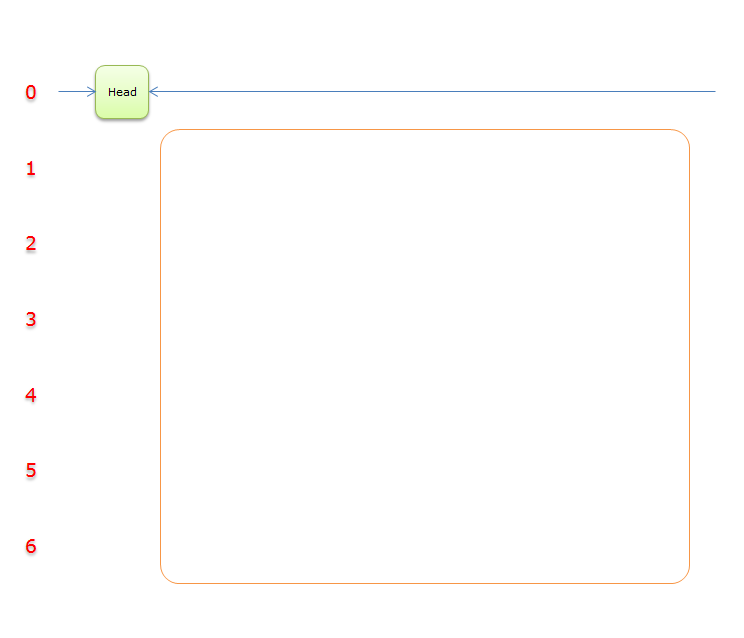
因为\(head.right=head\),故求解结束,答案栈中的答案分别是\(4、5、1\),表示该问题的解是第\(4、5、1\)行覆盖所有的列,即下图蓝色的部分
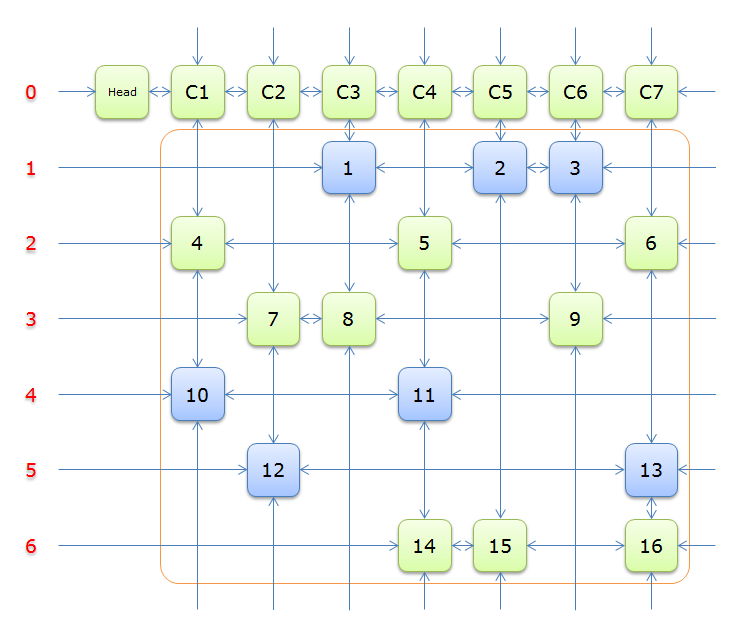
总结\(Dancing Links\)的求解
- 函数入口
- 判断$head.right \space ?= head $,若成立,输出答案,返回已解决,退出函数
- 获得\(head.right\)的元素\(C\)
- 标示元素\(C\)
- 获得元素\(C\)所在列的一个元素
- 标示该元素同行的其他元素所在的列首元素
- 获得一个简化问题,递归,若返回已解决,则退出函数
- 若刚刚尝试的不行,回标该元素同行的其他元素所在的列首元素,回标顺序与之前标示的顺序相反
- 获得元素\(C\)所在列的下一个元素,若有,跳转“标示该元素同行的其他元素所在的列首元素”
- 若没有,回标元素\(C\),返回未解决,退出函数
例题 P4929
代码实现
#include"bits/stdc++.h"
using namespace std;
const int N=250015;//N*M
#define inl inline
#define reg register
#define regi register int
#define PII pair<int,int>
inl int read(void)
{int x=0,f=1;char ch=getchar();while(!isdigit(ch)) f=ch=='-'?-1:f,ch=getchar();while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;
}
int l[N],r[N],up[N],down[N],col[N],row[N];//每个点的左右上下指针,以及每个点所在的行列
int head[N];int sz[N];//每行的头结点,每列的节点数
int ans[N];//答案栈
int n,m,cnt;
void build(int m)
{for(int i=0;i<=m;i++) r[i]=i+1,l[i]=i-1,up[i]=down[i]=i;r[m]=0,l[0]=m;memset(sz,0,sizeof sz);cnt=m+1;//已经处理了0行,从第一行开始insert
}
void insert(int R,int C)//在R行C列插入点
{sz[C]++;row[++cnt]=R,col[cnt]=C;up[cnt]=C,down[cnt]=down[C];up[down[C]]=cnt,down[C]=cnt;if(!head[R]) head[R]=r[cnt]=l[cnt]=cnt;else r[cnt]=head[R],l[cnt]=l[head[R]],r[l[head[R]]]=cnt,l[head[R]]=cnt;
}
void remove(int C)//删除C列的集合
{r[l[C]]=r[C],l[r[C]]=l[C];for(int i=down[C];i!=C;i=down[i])for(int j=r[i];j!=i;j=r[j])up[down[j]]=up[j],down[up[j]]=down[j],sz[col[j]]--;
}
void resume(int C)//恢复C列的集合
{for(int i=up[C];i!=C;i=up[i])for(int j=l[i];j!=i;j=l[j])up[down[j]]=down[up[j]]=j,sz[col[j]]++;r[l[C]]=C,l[r[C]]=C;
}
bool dance(int dep)
{if(r[0]==0)//head.right=head{for(int i=0;i<dep;i++) printf("%d ",ans[i]);return 1;}int C=r[0];for(int i=r[0];i;i=r[i]) if(sz[i]<sz[C]) C=i;//找到点最少的列(优化)remove(C);for(int i=down[C];i!=C;i=down[i]){ans[dep]=row[i];//压入答案栈for(int j=r[i];j!=i;j=r[j]) remove(col[j]);if(dance(dep+1)) return 1;for(int j=l[i];j!=i;j=l[j]) resume(col[j]);}resume(C);return 0;
}
int main(void)
{n=read(),m=read();int s;build(m);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){s=read();if(s) insert(i,j);}if(!dance(0)) puts("No Solution!");//无解return 0;
}