(彩蛋:大样例是从数据里扒的,且没有绑点)。
由于组题人电脑坏了,所以只能写简略题解了(其实是组题人的口胡碎碎念),写的不清晰的和部分分可以听讲题(可能有一些地方我下意识省略了,可以来问我).
首先,生成到完美的时间线的概率是固定的,如果我们假设概率为
那么期望次数显然为 \(\frac{1}{p}\).
此时如果暴力去枚举所有生成树就可以拿到一些暴力分.根据暴力实现的美观程度可以拿到 \(20 \sim 34\) 分不等,比较优秀的暴力可以在较短时间内表出 \(n=10\),可以拿到 \(38\) 分.
对于 \(m=1\),显然树的形态是节点 \(1\) 连接着一个唯一的节点,这个节点再连接其他节点.有 \(n-1\) 种方案.难点在于树的总数.运用 prufer 序列知识可以得到是 \(n^{n-2}\).于是可以拿到 \(50\) 分.
以上是乱搞,接下来要向正解靠近了.
灵光一闪
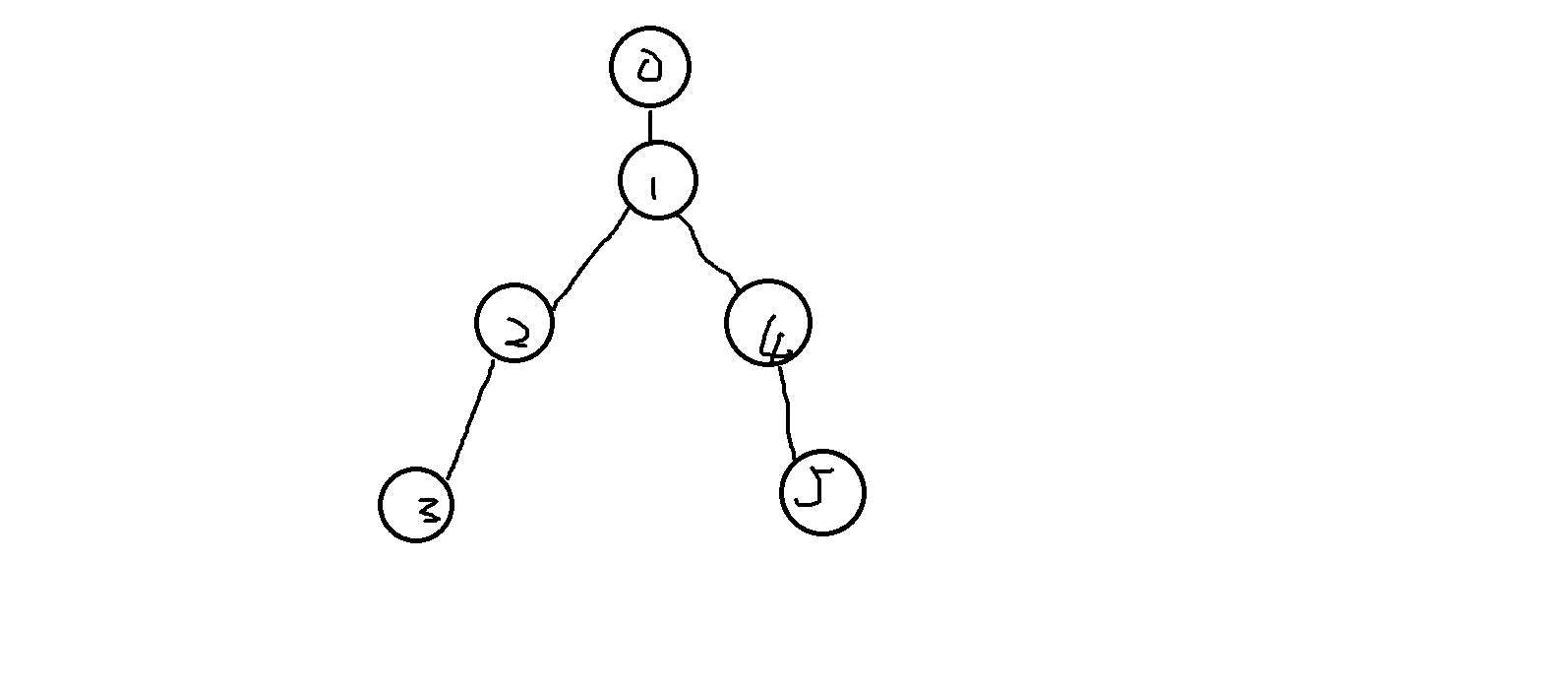
一个比较拉玛努金的思考点是把奇数深度点与偶数深度点分为两个部分,由于奇数点的邻接点一定是偶数点(偶数点的邻接点也一定是奇数点),所以构成了二分图.(实际上组题人在做这题时也没有想到这个点,但是可以用别的方法做,详见后文)
具体来说,左半部分(奇数点)包含了 \(1\) 和另外 \(n-m-1\) 个点(一共有 \(m\) 个偶数点和 \(n-m\) 个奇数点),右半部分是 \(m\) 个点.这样的二分图有 \(\binom{n-1}{m}\) 个.
对于每个二分图,我们要计算其生成树个数.
方法1
考虑这个完全二分图的生成树个数可以用 Matrix Tree Theorem.直接写出这个完全二分图的 laplace 矩阵 \(L(G)\):
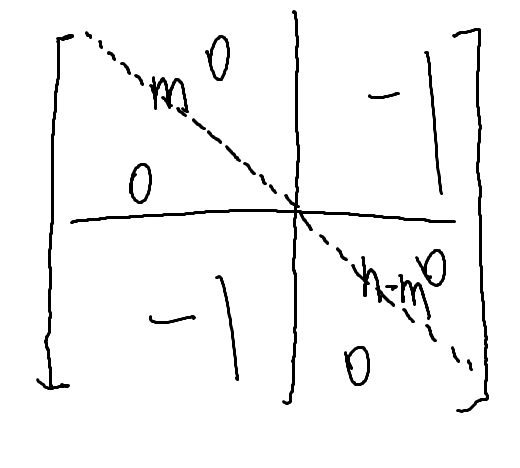
答案即为 \(\det L(G)\begin{pmatrix}1,2,\cdots,n-1 \\ 1,2,\cdots,n-1\end{pmatrix}\)
所以,生成树个数即为 \(\binom{n-1}{m}\det L(G)\begin{pmatrix}1,2,\cdots,n-1 \\ 1,2,\cdots,n-1\end{pmatrix}\).
使用高斯消元可以做到 \(O(n^3)\),可以拿到 \(70\) 分。
另外注意到 \(L(G)\begin{pmatrix}1,2,\cdots,n-1 \\ 1,2,\cdots,n-1\end{pmatrix}\) 的行和以及列和都是定值,我们可以手动把这个矩阵消成上三角。
最后得到 \(\det L(G)\begin{pmatrix}1,2,\cdots,n-1 \\ 1,2,\cdots,n-1\end{pmatrix} = m^{n-m-1}(n-m)^{m-1}\)。
答案即为 \(\binom{n-1}{m}m^{n-m-1}(n-m)^{m-1}\)
方法2
根据网络上的信息,我们可以直接用 prufer 做。
由于奇数点父亲一定是偶数点,所以偶数点在序列中出现了 \(n-m-1\) 次,同理奇数点出现了 \(m-1\) 次。
故答案为 \(\binom{n-1}{m}m^{n-m-1}(n-m)^{m-1}\)。
如果你没想到二分图
实际上这是组题人唯一想到的方法。
考虑把树放入集合 \(T\) 中,用 \(x\) 计数奇数点,\(y\) 计数偶数点。
可以得到 \(T=x\exp(y\exp{T})\)。
做完了,去™的二分图。

![pip install volcengine-python-sdk[ark]](https://img2024.cnblogs.com/blog/1892858/202409/1892858-20240923115039808-1785470606.png)