1.回溯算法的核心思想
回溯算法的核心思想是:尝试+记录+回退。
先尝试一种选项,在选择该选项的前提下继续寻解,如果最后寻解成功,则记录这个解,否则不用记录,然后再回退到选择该选项前的状态,改为尝试其它选项再继续寻解,判断其它选项是不是解。
2.回溯算法的关键点
回溯算法用于寻找全部解的集合,这些解满足共同的条件。我们先以"N皇后"为例分析下什么是回溯算法。
"N皇后"问题是在一个N*N的棋盘中,将N个棋子放到合适位置,满足任意两个棋子不在同一行、不在同一列、不在主对角线或次对角线上。下图是一个N为4的棋盘,其中Q表示棋子,#表示空格,满足条件。

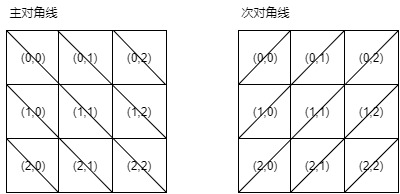
主对角线是从左上角到右下角的线,次对角线是从右上角到左下角的线,如下图所示
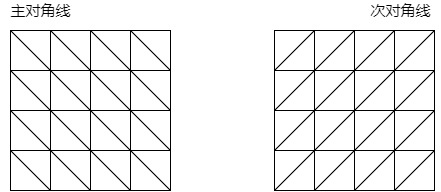
我们可以按照行逐次选择位置放置Q,最终结果肯定是每行有且仅有一个Q。
- 每行可以选择的列号为[0,1,...,N-1],这就是选项集合;
- 从[0,1,...,N-1]按照先后顺序选择一个位置,记为K,这个K是否满足"所在列无Q、所在主对角线无Q、所在次对角线无Q",这三个条件就是判断选项是否有效的限制条件(因为是按行取,每次只能尝试一个位置,所以每行不可能同时存在多个Q,不用判断"所在行无Q")。
- 每次尝试一个选项后,棋盘布局和三个限制条件都需要更新。这里棋盘的布局就是动态变化的状态。当该状态满足棋盘行数达到N,则说明找到了一个解。
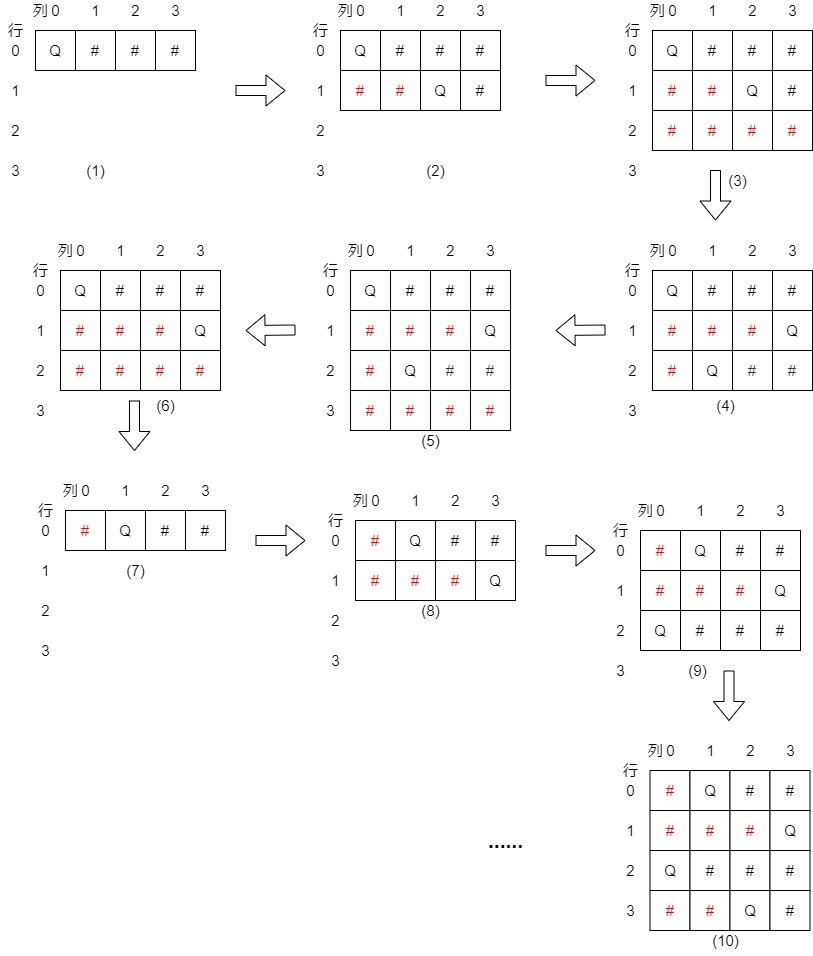
如下图所示,展示回溯过程:
- 首先行0选择(0,0);
- 行1的(1,0)和(1,1)不满足限制条件,尝试选项(1,2);
- 行2所有选项都不满足限制条件,说明前面行0和行1那样选择不行,回退到行1取消选项(1,2),尝试
选项(1,3),行2选择(2,1); - 行3所有选项都不满足限制条件,说明前面行0、行1和行2那样选择不行,回退到行2,行2剩余的(2,2)和(2,3)都不行,继续回退到行1,行1没有剩余选项,继续回退到行0,行0尝试选项(0,1),新一轮开始。
- 行1选择(1,3);
- 行2选择(2,0);
- 行3选择(3,2),棋盘行数达到4,所以找到一个解,记录该解。回退最近尝试的选项,回退到行3选择(3,3),不满足限制,故继续回退到行2,通过这种尝试、记录、回退的方法可以找到所有解。
通过上面例子,相信你已经对回溯算法有了自己的理解,回溯算法关键信息包括如下:
1>可以尝试的选项集合。
2>用于判断一种选项是否是有效的限制条件。
3>尝试新的有效选项后,更新状态。
4>继续寻找。
5>状态达到为解需要满足什么解条件。如果是解,需要记录这个解。
6>尝试完成后再回退到该尝试前的状态。
3.伪代码
几乎所有的回溯算法代码都可以使用下面的代码框架:
/**result:所有解的集合.*state:状态.*choices:选项集合.*constraint:限制条件.*/
void backtrack(vector<State> &result,State &state,vector<Choice>&choices,Constraint &constraint)
{if(isSolution(state)) //当前state是解{recordSolution(result,state);//记录这个解到resultreturn; //回退}for(auto choice:choices) //按先后顺序遍历选项{if(isValidChoice(choice,constraint)) //选项有效{tryChoice(state,constraint); //尝试该选项backtrack(result,state,choices,constraint); //继续回溯roolbackChoice(state,constraint); //回退该选项}}
}
4.代码实现
上面"N皇后"问题代码实现如下:
class Solution
{
private:int s_row; //当前处理的行号int m_size; //棋盘大小vector<int> m_colPostionS; //表示可选择的列vector<bool> m_colConstrain; //表示每列是否有Qvector<bool> m_mDiagonalConstrain;//表示每个主对角线上是否有Qvector<bool> m_sDiagonalConstrain;//表示每个次对角线上是否有Q
public:int solveNQueues(int n) {s_row=0;m_size=n;m_colPostionS.resize(m_size);for(int i=0;i<m_size;++i)m_colPostionS[i]=i;m_mDiagonalConstrain.resize(2*n-1,false);m_sDiagonalConstrain.resize(2*n-1,false);m_colConstrain.resize(n,false);//vector<vector<string>> chessboard;vector<vector<vector<string>>> res;backtrackMy(chessboard,res,m_colPostionS,m_colConstrain,m_mDiagonalConstrain,m_sDiagonalConstrain);return res.size();}
//判断解bool isSolution(vector<vector<string>> &state){if (!state.empty() && state.size()==m_size)//解条件return true;return false;}
//记录解
void recordSolution(vector<vector<string>> &state,vector<vector<vector<string>>> &res)
{res.emplace_back(state);
}
//判断选项有效
bool isValidChoice(int row,int col,vector<bool> &colConstrain,vector<bool> &mDiagonalConstrain,vector<bool> &sDiagonalConstrain)
{if(colConstrain[col]==true || mDiagonalConstrain[row+col]== true || sDiagonalConstrain[row-col+m_size-1]==true)return false;return true;
}
//尝试选项
void tryChoice(vector<vector<string>> &state,int row,int col,vector<bool> &colConstrain,vector<bool> &mDiagonalConstrain,vector<bool> &sDiagonalConstrain)
{vector<string>tempRow(m_size,"#");tempRow[col]="Q";state.emplace_back(tempRow);colConstrain[col]=true;sDiagonalConstrain[row+col]=true;mDiagonalConstrain[row-col+m_size-1]=true;
}
//回退选项
void roolbackChoice(vector<vector<string>> &state,int row,int col,vector<bool> &colConstrain,vector<bool> &mDiagonalConstrain,vector<bool> &sDiagonalConstrain)
{state.pop_back();colConstrain[col]=false;sDiagonalConstrain[row+col]=false;mDiagonalConstrain[row-col+m_size-1]=false;}
//使用按行放置的策略
//棋盘上"Q"表示皇后,"#"表示空位置
//colPostionS是choices
//state表示棋盘
//res表示最终结果
void backtrack(vector<vector<string>> &state, vector<vector<vector<string>>> &res,vector<int> &colS,vector<bool> &colConstrain,vector<bool> &mDiagonalConstrain,vector<bool> &sDiagonalConstrain)
{if (isSolution(state))//检查是否为解 {recordSolution(state, res);//记录解return;}for (int col : colS) // 遍历所有选择{if (isValidChoice(s_row,col,colConstrain,mDiagonalConstrain,sDiagonalConstrain))//有效 {// 尝试:做出选择,更新状态tryChoice(state,s_row++,col,colConstrain,mDiagonalConstrain,sDiagonalConstrain);//注意对s_row的处理// 进行下一轮选择backtrack(state, res,colS,colConstrain,mDiagonalConstrain,sDiagonalConstrain);// 回退:撤销选择,恢复到之前的状态roolbackChoice(state,--s_row,col,colConstrain,mDiagonalConstrain,sDiagonalConstrain);//注意对s_row的处理}}
}
};
说明:
大小为N的棋盘,其主对角线和次对角线个数都为2N+1条。如下图所示N为3为例:
- 每条主对角线上元素的行号减去列号是一样的,即row-col分别为[-2,-1,0,1,2]。即row-col+N-1对应[0,1,2,3,4]。
- 每条次对角线上元素的行号加上列号是一样的,即row+col分别为[0,1,2,3,4]