A 几何
重复若干次 -> 不能重叠,因此考虑直接暴力 DP
设 \(f_{i,j,k}\) 表示主串匹配到第 \(i\) 位(将前 \(i\) 位分别归为两类),其中 \(x\) 在重复了若干次后,又匹配到了第 \(j\) 位,\(y\) 在重复了若干次后,又匹配到了第 \(k\) 位
转移非常好写,枚举 \(i\),尝试把 \(s_{i}\) 分别与 \(x_{j},y_{k}\) 匹配,匹配上了就直接转移到 \(f_{i+1,j+1,k}(f_{i+1,j,k+1})\),或者在 \(j\operatorname{or}k=n\) 的时候直接赋成 \(0\)
复杂度是 \(O(nxy)\) 的,一算 \(10^{9}\),注意到这个东西完全不挂常数,考虑稍微优化一下
endl 改 \n,代码生下来常数就小的直接过了
否则的话考虑直接 bitset(能 bitset 是因为这题的 dp 数组全是 bool,转移也全是或运算),预处理出 \(x,y\) 中能参与 \(s_{i}\) 的转移的位置,然后直接 bitset 做就能砍到差不多 \(2\times 10^{8}\)
还过不了就是孩子代码一生下来常数就大
解决方案:手写一个用 ull 压
#include<bits/stdc++.h>
using namespace std;
#pragma GCC optimize(3)
#define endl '\n'
int cases;
string s,x,y;
bool f[2][51][51];
// 0:x 1:y
int main(){ios::sync_with_stdio(false);freopen("geometry.in","r",stdin);freopen("geometry.out","w",stdout);cin>>cases;while(cases--){cin>>s>>x>>y;f[0][0][0]=1;for(int i=1;i<=(int)s.length();++i){for(int j=0;j<=(int)x.length();++j){for(int k=0;k<=(int)y.length();++k){f[i&1][j][k]&=0;}}for(int j=0;j<=(int)x.length();++j){for(int k=0;k<=(int)y.length();++k){if(j!=0 and s[i-1]==x[j-1]){f[i&1][j!=(int)x.length()?j:0][k!=(int)y.length()?k:0]|=f[(i-1)&1][j-1][k!=(int)y.length()?k:0];}if(k!=0 and s[i-1]==y[k-1]){f[i&1][j!=(int)x.length()?j:0][k!=(int)y.length()?k:0]|=f[(i-1)&1][j!=(int)x.length()?j:0][k-1];}}}}if(f[((int)s.length())&1][0][0]==true){cout<<"Yes"<<endl;}else{cout<<"No"<<endl;}}
}
/*
abaaabbaab
1112112122[1 0]
[2 0]
[3 0]bbaabaabaaabaabaab
221111111121111111[2,0]
bba
aab
*/
B
我说我的爆搜为什么不对,拉下来对拍拍出一组十字架图
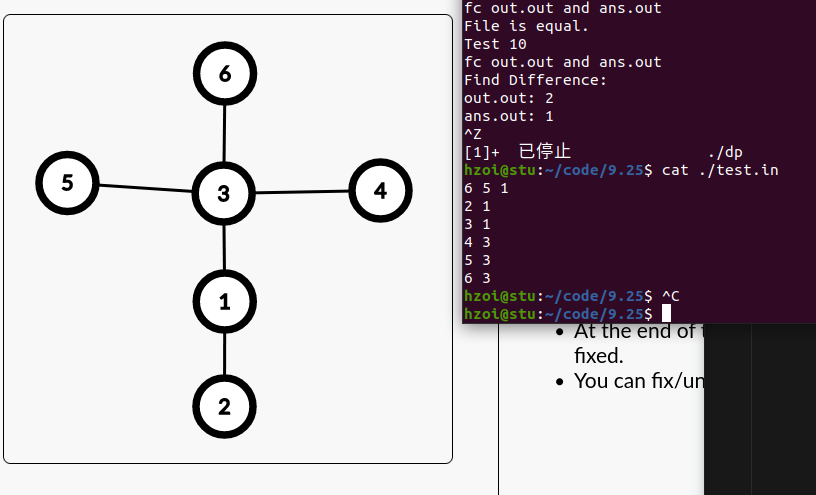
因为我一开始觉得删边等于删点,所以我就每次路过把点删了,但是事实上不是这样,所以这题 \(n^{2}\) 的搜完全不可做
因为题目里这么走,相当于走了一个欧拉路,然而欧拉路是要求最多两个节点是奇点,因此考虑转移问题为使原图变为欧拉路
设 \(f_{i,0/1,0/1}\) 表示考虑到 \(i\) 和它的子树,\(i\) 自己是不是奇点,\(i\) 和 \(i\) 的子树里有没有奇点的最小花费,然后做树形 DP
首先,操作 \(A\) 相当于加重边,作用为可以使两边的节点中奇边变成偶边,偶边变成奇边,并且可以对两颗子树进行合并
假如我们把 \(j\) 合并到 \(i\) 上,合并后 \(j\) 就是 \(i\) 的子树,,设由 \(f_{i,k,l},f_{j,m,n}\) 转移,那么新的转移方程中的第三项就应该是 \(l\operatorname{or}m\operatorname{or}n\),即 \(i\) 和 \(j\) 只要有一个的子树存在奇点,那么合并后 \(i\) 的子树就存在奇点
接下来看 \(B\) 操作,考虑 \(B\) 的贡献变化量,有一结论使得 \(B\) 操作变化量与奇点数量变化量正相关,即 \(\lfloor\) 奇点数量除二 \(\rfloor\) 减一 \(=B\) 操作数量,不会证不放了
如果我们执行 \(B\) 操作的两个点都是奇点,那么直接瞬移,这两个点之间就不需要连边了,可以看成两个奇点都变成了偶点,所以 \(B\) 操作总数减一
如果两个点全是偶点,本来能自己过去,非要瞬移到另一边,现在过不去了,还要再瞬移回来,所以会让 \(B\) 操作加一
否则,实际上瞬移一下没啥变化,\(B\) 不变
统计答案的时候,原图可以是欧拉回路,或者可以存在两个奇点(此时需要一次瞬移),注意这个奇点不一定非要有一个在根节点上
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,a,b;
vector<int>e[500001];
const int inf=LLONG_MAX/10;
int f[500001][2][2],g[2][2];
void dfs(int now,int last){f[now][0][0]=0;f[now][0][1]=inf;f[now][1][0]=inf;f[now][1][1]=inf;for(int i:e[now]){if(i!=last){dfs(i,now);for(int j=0;j<=1;++j){for(int k=0;k<=1;++k){g[j][k]=f[now][j][k];f[now][j][k]=inf;}}for(int j=0;j<=1;++j){for(int k=0;k<=1;++k){for(int l=0;l<=1;++l){for(int m=0;m<=1;++m){f[now][j][k|l|m]=min(f[now][j][k|l|m],g[j][k]+f[i][l][m]+a);int cost=0;if(!j and !l) cost=b;else if(j and l) cost=-b;f[now][1-j][k|(1-l)|m]=min(f[now][1-j][k|(1-l)|m],g[j][k]+f[i][l][m]+cost);}}}}}}
}
signed main(){freopen("analyse.in","r",stdin);freopen("analyse.out","w",stdout);cin>>n>>a>>b;for(int i=1;i<=n-1;++i){int x,y;cin>>x>>y;e[x].push_back(y);e[y].push_back(x);}dfs(1,0);cout<<min({f[1][0][0],f[1][1][1]-b,f[1][0][1]-b});
}
D 组合
神秘题,但是我觉得这个思路还是很好的
首先因为不会对你的询问返回答案,也就意味着没办法用类似二分的方法求解,否则会被卡成完全二叉树
题目让我们构造 \(m\) 个 \(N\) 位二进制数,考虑转化成 \(N\) 个 \(m\) 位二进制数,每次询问相当于询问一竖列
只考虑其中的三组二进制数,发现这三组有贡献的条件是两两位或结果不同,证明:设 \(a\operatorname{or}b=a\operatorname{or}c\),对于竖列的询问,若 \(a_i\operatorname{or}b_i=a_i\operatorname{or}c_i=1\),则对于任何一组询问都返回 \(1\),若 \(a_i\operatorname{or}b_i=a_i\operatorname{or}c_i=0\),则对于任何一组询问都返回 \(0\),没有区分的意义,所以要求全部二进制数两两位或运算不同
然后就到了神秘的地方,怎么构造这 \(N\) 个二进制数
STD 的做法是枚举 \(8\) 位和 \(9\) 位的二进制数(这里指的是二进制数中 \(1\) 的个数),暴力判断能不能放进去,能放就放
这个 \(8\) 和 \(9\) 太神秘了,不知道他咋出的,在 \(N=1000\) 的时候正好能卡到 \(m=26\),我改了参之后再跑,发现从 \(4\) 位开始跑贼慢,跑了三个小时才七百多个,从 \(15\) 位开始跑就莫名其妙寄了,好像是跑不出来答案卡死循环了
好在结论题比较好改
STD
#include<bits/stdc++.h>
using namespace std;
int N = 20;
int a[1015];
bitset<1073741824> bk;
int main() {int cur = 0;vector<int> vec;for (int i = 0; i < (1 << N); i++) {if (__builtin_popcount(i) == 8)vec.push_back(i);}for (int i = 0; i < (1 << N); i++) {if (__builtin_popcount(i) == 9)vec.push_back(i);}for (int i = 1; i <= 1010; i++) {bool fl2 = 0;for (auto t : vec) {a[i] = t;bool fl = 0;for (int j = 1; j <= i; j++) {if (bk[a[i] | a[j]] || (i != j && i <= 996 && __builtin_popcount(a[i] | a[j]) < 11)) {fl = 1;for (int k = 1; k < j; k++)bk[a[i] | a[k]] = 0;break;}bk[a[i] | a[j]] = 1;}if (fl)continue;fl2 = 1;break;}if (!fl2) {N++;vec.clear();for (int j = 0; j < (1 << N); j++) {if (__builtin_popcount(j) == 8)vec.push_back(j);}if (N >= 24) {for (int j = 0; j < (1 << N); j++) {if (__builtin_popcount(j) == 9)vec.push_back(j);}}if (N == 26) {for (int j = 0; j < (1 << N); j++) {if (__builtin_popcount(j) != 8 && __builtin_popcount(j) != 9)vec.push_back(j);}}i--;continue;}cout << i << ' ' << N << endl;if (N > 26) {cur = i - 1;break;}}freopen("output.txt", "w", stdout);for (int i = 1; i <= 1000; i++)cout << a[i] << ',';cout << endl;return 0;
}
#include<bits/stdc++.h>
using namespace std;
int a[]; //自己去跑 STD
string to_binary(int x){string ans;while(x){if(x&1) ans.push_back('1');else ans.push_back('0');x>>=1;}// cout<<"::"<<ans<<endl;while(ans.size()<26) ans.push_back('0');reverse(ans.begin(),ans.end());return ans;
}
vector<string>ans(27);
int main(){ofstream cth("combination.out");for(int i=0;i<=999;++i){string as=to_binary(a[i]);// cout<<as<<endl;for(int j=0;j<=25;++j){ans[j].push_back(as[j]);}}cth<<26<<endl;for(int i=0;i<=25;++i){cth<<ans[i]<<endl;}
}
冬日绘版