大语言模型(LLM)的推理能力可以通过测试时聚合策略来改进,即为每个问题生成多个样本并对它们进行聚合以找到更好的答案。这些方法往往会达到饱和点,超过这个点后额外的样本不会带来更多收益。精炼(refinement)提供了另一种选择,它使用模型生成的反馈不仅采样更多解决方案,还提高它们的质量。但是精炼引入了三个关键挑战:
(1)过度精炼:对所有实例进行统一精炼可能导致过度校正并降低整体性能。
(2)无法定位和解决错误:LLM自我纠正能力有限,难以以有针对性的方式识别和纠正自己的错误。
(3)精炼不足:确定需要多少轮精炼并非易事,过早停止可能会导致错误未得到解决。
为了解决这些问题,论文提出了MAGICORE,一个用于粗到细精炼的多代理迭代框架。MAGICORE旨在通过将问题分类为简单或困难,为简单问题使用粗粒度聚合,为困难问题使用细粒度和迭代多代理精炼,从而避免过度精炼。
主要贡献
- 提出了MAGICORE,一个多代理粗到细框架,自适应地使用有针对性的反馈,在所有样本预算下都优于Self-Refine等精炼方法,以及Best-of-k和Self-Consistency等聚合方法,跨五个数据集和两个LLM模型都取得了优异表现。
- 所提出的难度感知粗到细资源分配方法具有样本效率,即使使用8倍少的样本也优于k-way SC。
- 分析表明纳入奖励模型(RM)用于精炼是必要的,相比训练好的现成RM,LLM单独在确定何时需要精炼方面效果较差。
- 验证了虽然所使用的精炼基线在多次迭代中没有显示出改进,但MAGICORE随着额外迭代持续改进。
精炼面临的问题
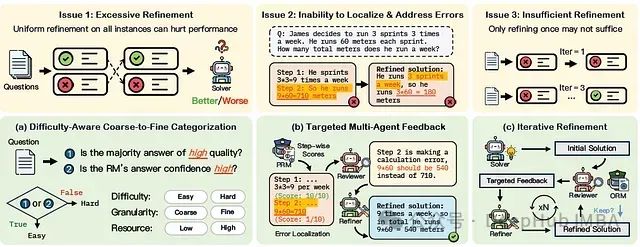
- 问题1:过度精炼- 精炼存在过度校正的风险,可能将正确的解决方案变成错误的。
- 问题2:无法定位和解决错误- LLM自我纠正能力有限,难以以有针对性的方式识别和纠正自己的错误。
- 问题3:精炼不足- 有效的精炼应该逐步改善输出,但过早停止可能会导致错误未得到纠正。
https://avoid.overfit.cn/post/de94cdefa04645f19f9ede3b85a138f9




CSP-S 联训模拟 1](https://img2024.cnblogs.com/blog/3389876/202409/3389876-20240926082535677-413473993.png)
