赛时草了个 \(O(n^4 \log (n))\) 竟然能过 70 分虽然本来就是这么分配的,发现正解只需将二分改为双指针就可以了,最气的是上面计算的时候用到还是尺取下面就用的二分(唐诗)。
其实这题就是暴力,然后在低级的暴力上加一些操作变得稍微高级一点。
计算的话直接暴力查找不同颜色,只不过范围由小变大时只需扩展外围即可,例如下面的示例图。
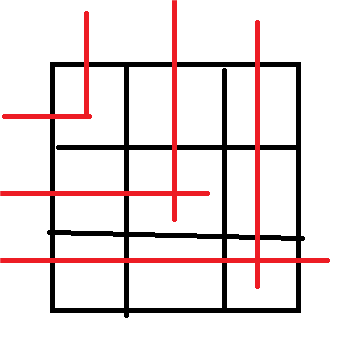
这样扩展的话每次只会扩展外围,所以复杂度为 O(n) 的扩展,总复杂度为 O(n^3) ,然后就没了,不知道为什么唐诗的我没写出来。
#include<bits/stdc++.h>
using namespace std;
const int N=505;
int n,m;
int a[N][N];
int b[N][N];
int vis[N];
int main(){ios::sync_with_stdio(false);freopen("square.in","r",stdin);freopen("square.out","w",stdout);cin>>n>>m;int cnt=0;for(int i=1;i<=n;i++){b[i][n]=1;b[n][i]=1;for(int j=1;j<=n;j++){cin>>a[i][j];} }for(int i=n-1;i>=1;i--){for(int j=1;j<=n-1;j++){cnt=0;memset(vis,0,sizeof vis);for(int p=0;i+p<=n&&j+p<=n;p++){for(int k=0;k<=p;k++){if(!vis[a[i+p][j+k]]){vis[a[i+p][j+k]]=1;cnt++;}if(!vis[a[i+k][j+p]]){vis[a[i+k][j+p]]=1;cnt++;}}if(cnt>m){break;}b[i][j]=p+1;}}}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cout<<b[i][j]<<" ";}cout<<"\n";}return 0;
}



![电影《749局》迅雷BT下载/百度云下载资源[MP4/2.12GB/5.35GB]超清版](https://img2024.cnblogs.com/blog/3514446/202410/3514446-20241001142111253-1293388443.jpg)
![电影《749局》迅雷百度云下载资源4K分享[1.16GB/2.72GBMKV]高清加长版【1280P已完结】](https://img2024.cnblogs.com/blog/3514446/202410/3514446-20241001142336788-1614095886.jpg)


![[rCore学习笔记 028] Rust 中的动态内存分配](https://img2024.cnblogs.com/blog/3071041/202410/3071041-20241001133558797-252701878.png)
