1 培养数学直觉

我们最初接触一个概念时,会形成我们的直觉。而我们的直觉会影响我们对一门学科的喜爱程度。什么意思呢?
假设我们想给 “猫 ”下一个定义:
- 古代的定义: 一种毛茸茸的动物,有爪子、牙齿、尾巴和四条腿,高兴时发出咕噜声,生气时发出嘶嘶声。
- 进化定义: 某一物种(猫科动物)的哺乳动物后代,具有某些共同特征。
- 现代定义: 你管这些叫定义?猫是具有以下 DNA 的动物:ACATACATACATACAT。
现代定义的确很精确。但它是最好的吗?你会教给学习这个词的孩子吗?它是否能让人更好地了解这种动物的 “猫性”?
动物的 “猫性”?其实不然。现代定义是有用的,但在了解了猫是什么之后。这不应该是我们的起点。
不幸的是,对数学的理解似乎也遵循着 DNA 的模式。我们学到的是现代的、严谨的定义,而不是导致这一定义的见解。
我们只掌握了神秘的公式(DNA),却对数学思想知之甚少。

1.1 什么是圆?
是时候举个数学例子了: 如何定义圆?
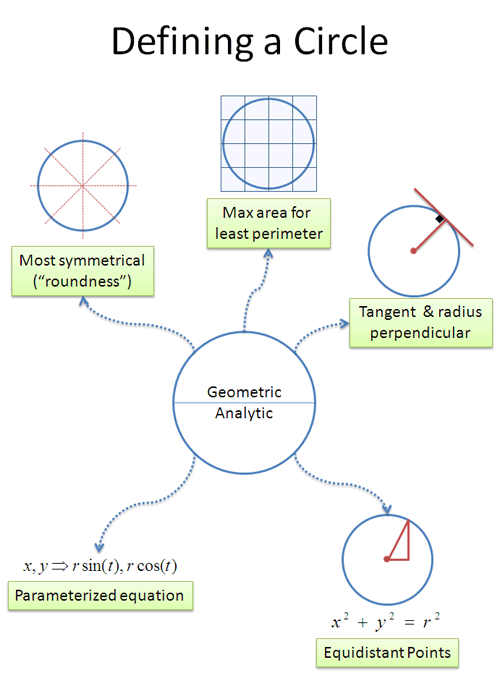
似乎有数不清的定义。下面是一些定义
- 可能的最对称的二维形状
- 以最小的周长获得最大面积的形状(等周周长性质)
- 平面上的所有点到给定点的距离相同(用圆规或铅笔画在绳子上)
- 方程 x^2 + y^2 = r^2 中的点(x,y)(上述地理公制定义的解析版本
公制定义的解析版) - 方程 r - sin(t)、r - cos(t)中的点,适用于所有 t(真正的解析版本)
- 切线始终垂直于位置矢量的形状(物理解释)
这样的例子不胜枚举,但关键在于:这些事实描述的都是同一个概念!这就像说 1、one、uno、eins、“2x + 3 = 5 的解 ”或 “你脸上鼻子的数量”--只是对统一概念的不同称呼。
但这些最初的描述非常重要--它们塑造了我们的直觉。因为我们在课堂之前就在现实世界中看到过圆,所以我们理解了圆的 “圆度”。无论我们看到什么花哨的等式(x^2 + y^2 = r^2),我们内心深处都知道圆是圆的。如果我们把这个等式画成图形,它看起来是方的,或者是一边倒的,我们就会知道这是个错误。
在孩提时代,我们学习了古代人对圆的定义(一个真正圆的东西),这给了我们一种舒适的直觉。我们可以看到,“圆东西 ”上的每一点到圆心的距离都是一样的。
x^2 + y^2 = r^2是表达这一事实的解析式(使用毕达哥拉斯距离定理)。我们从一个角落开始,凭着直觉,一步一步地得出了正式定义。
参考资料
- 软件测试精品书籍文档下载持续更新 https://github.com/china-testing/python-testing-examples 请点赞,谢谢!
- 本文涉及的python测试开发库 谢谢点赞! https://github.com/china-testing/python_cn_resouce
- python精品书籍下载 https://github.com/china-testing/python_cn_resouce/blob/main/python_good_books.md
- Linux精品书籍下载 https://www.cnblogs.com/testing-/p/17438558.html
1.2 培养洞察力的策略
数学是关于思想的,公式只是表达思想的一种方式。一旦中心概念明确了,方程式就会水到渠成。下面是一个对我有帮助的策略:
- 第一步:找到数学概念的中心主题。这可能很难,但可以尝试从它的历史入手。这个概念最早是在哪里使用的?发现者在做什么?这种使用可能与我们现代的解释和应用不同。
- 步骤 2:用主题解释一个性质/事实。用主题来类比正式定义。如果幸运的话,你可以将数学公式 (x^2 + y^2 = r^2)转换成通俗易懂的语言(“所有点到中心的距离相同”)。
- 第三步:利用同一主题探索相关性质。一旦你有了一个有效的类比或解释,看看它是否适用于其他性质。有时适用,有时不适用(你需要新的见解),但你会有意想不到的发现。
1.3 一个真实的例子:
e在科学中随处可见,有无数的定义,但却很少以自然的方式出现。让我们围绕这个想法来建立一些洞察力。以下部分有几个
等式,这些等式只是描述想法的方法。即使等式是胡言乱语,其背后也有一个通俗易懂的概念。下面是一些常见的e的定义:
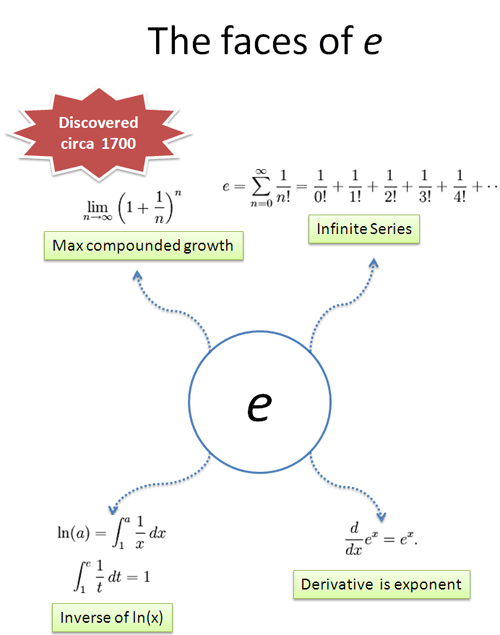
第一步是找到主题。纵观 e 的历史,它似乎与经济增长或利率有关。e 是在进行商业计算(而不是抽象的数学猜想)时发现的,因此 “利息”(增长)是一个可能的主题。
事实上,这就是复利计算公式,即在 1 个单位时间内以最快速度复利计算 100%的利息。
- 定义 1:将 e 定义为 100%的复利增长,以尽可能小的速度递增。
让我们来看看第二个定义:一个越变越小的无限项序列。这会是什么呢?
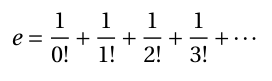
以 “利息 ”为主题对其进行推理后,我们发现这个定义显示了复利的组成要素。
这个定义显示了复利的组成部分。现在,洞察力并不是一蹴而就的--这个洞察力可能是在头脑风暴 "1 + 1 + ...
1/2 + 1/6 + . . . “代表什么?
那么,第一个项(1 = 1/0!,记住 0 是 1)就是你的本金,即原始金额。下一个项(1 = 1/1!)是你赚取的 “直接 ”利息--1 的 100%。下一个项(0.5 = 1/2!)是你的利息赚取的金额(“二级利息”)。下一个项(0.1666 = 1/3!)
是你的 “三级利息”--你的利息赚了多少钱!钱生钱,钱生钱,钱生钱,依此类推。
序列将这些贡献分开(“e ”一章描述了 “蓝先生”、“绿先生 ”和 “红先生 ”如何独立成长)。要说的还有很多,但这就是 “以成长为中心 ”对这一观点的理解。
- 定义 2:根据每项兴趣对 Neato 的贡献来定义 e。
现在来看第三个最简短的定义。它是什么意思呢?不要去想 “导数”(这会让你的大脑进入计算公式的模式),而是想想它意味着什么。等式的感觉。让它成为你的朋友。
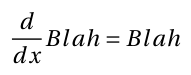
这是微积分的说法:“你的增长率等于你当前的数量”。那么,以你当前的金额增长就是 100%的利率,对吗?而 “一直在增长 ”意味着你一直在计算利息--这是另一种描述 “一直在增长 ”的方式。
这是连续复利的另一种描述方式!
-
定义 3:将 e 定义为始终以当前价值的 100%增长。
最后一个定义的时间到了--这是个棘手的问题。我是这样解释的:
与其描述你增长了多少,为什么不说花了多长时间呢?
如果你的增长速度是 100%,那么从 1 到 2 需要 1 个单位的时间,但一旦你的增长速度是 100%,达到了 2,就意味着你每单位时间的增长速度是 2 个单位!从 3 到 4 只需要 1/3 单位的时间,以此类推。
从 1 到 A 所需的时间就是 1 到 2、2 到 3、3 到 4......的时间。第一个定义定义了自然对数(ln),作为这种 “增长时间 ”计算的简称。
ln(a) 简单地说,就是从 1 增长到 a 所需的时间。换一种说法,e 就是在等待 1 个单位时间后的增长量! -
定义 4:把从 1 持续增长到 a 所需的时间定义为 ln(a)。
什么?这就是描述神秘 e 的四种不同方法。
一旦我们有了核心理念(“e 是 100% 的连续增长”),疯狂的方程就会水到渠成--微积分就可以翻译成英语了。
1.4 道理是什么?
在数学课上,我们常常从最后一个最复杂的思想开始。难怪我们会感到困惑:我们给学生看 DNA,却希望他们看到一只猫。
我从这种方法中汲取了一些教训,它是我理解和解释数学的基础。
理解和解释数学的方法:
- 寻找洞察力并加以应用。第一个直观的洞察力可以帮助其他所有的事情都水到渠成。从一个有意义的定义开始,“绕着圈子 ”寻找其他定义。
- 足智多谋。用脑袋去撞击一个想法并不好玩。如果它不适合你,那就从不同的角度去思考。有另一本书、另一篇文章、另一个人的解释对你有意义。
- 视觉化是可以的。我们认为数学是死板的、分析性的,但视觉解释也是可以的!做能加深理解的事。在最初发现虚数的几十年后,人们才发现它的几何解释。整天看方程式并不能帮助数学家 “理解 ”它们的含义。
当我们把注意力放在定义而不是理解上时,数学就会变得困难和令人沮丧。请记住,现代定义是最先进的思维步骤,而不一定是起点。不要害怕从一个有趣的角度去理解一个概念--找出等式背后的通俗易懂的句子。