电路中一个输出连接多个输入,需要提高输出门的驱动能力;若多个输出连接一个输入,则需要引入高阻态保证逻辑的正确性。一般 CMOS 的逻辑门单元理想状态下同一时刻总有一个连通,是无法输出高阻态的。输入高阻态需要特殊的器件,在 PDK 中一般以传输门或者三态buf方式实现。
MUX: 逻辑实现
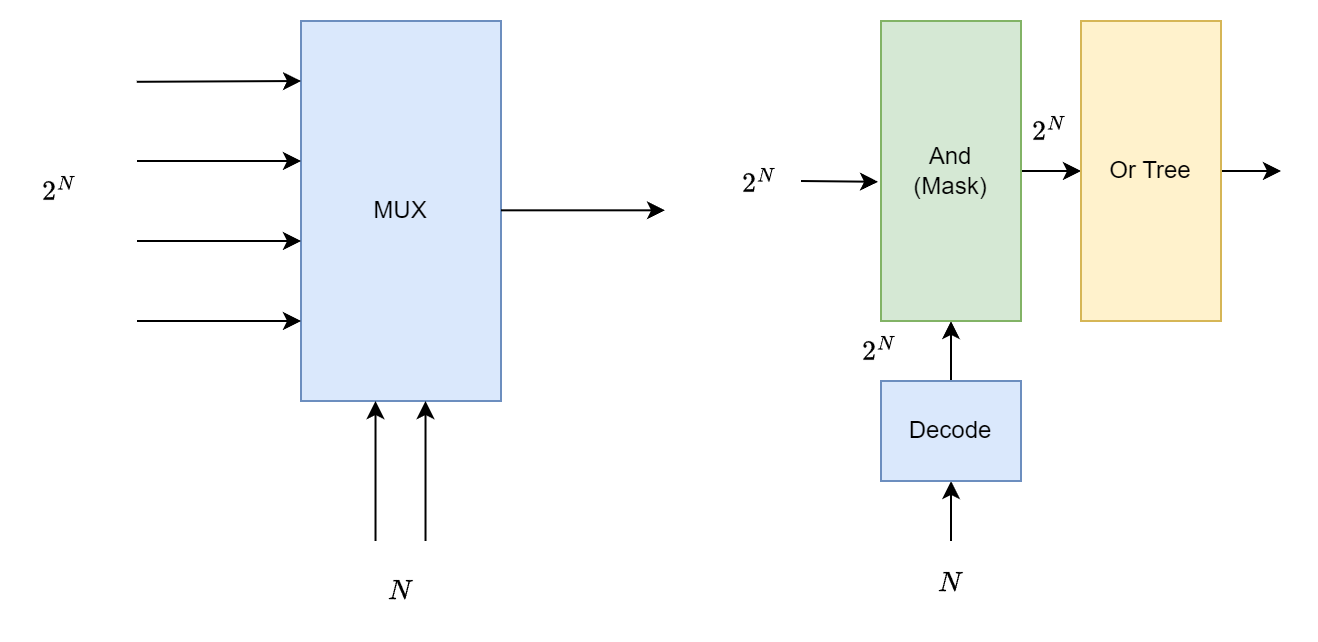
NUX 是最常见汇聚电路的信号元件,即可以使用三态也可以使用逻辑门实现。如图,MUX 拥有 \(N\) 位选择信号,\(2^N\) 待选择信号以及一位输出。实现上先用解码器将 \(N\) 位信号解码成 \(2^N\) 位,然后与待选择信号进行mask,最后通过或逻辑 tree 结构将信号汇聚。
想要将逻辑实现方式和 tri-state 方式比较,就要进一步量化实现所用开销。Mask 和 tree 分别使用了 \(2^N\) 和 \(2^N-1\) 个逻辑门,但一般量化 decode 的开销暂时还没有查询到相关资料,可能实践中这和 PDK 设计以及具体 EDA 过程高度相关。但无妨本文中先假设提出一个泛化的实现笼统感受开销差距。
从布尔运算结果看, decode 的每个输出都是 N 个变量进行与,如 \(ABC\bar{D}\)。所以每个输出都可以用 \(N-1\) 个与门构成,附之生成取反的非门,一共是 \(N\) 个非门以及 \(2^N\times (N-1)\) 个与门。
但若观察输出,发现有很多信号可以共用,并不需要重复生成。比如 \(ABC\bar{D}\) 和 \(AB\bar{C}D\),就可以共用 \(AB\) 信号。
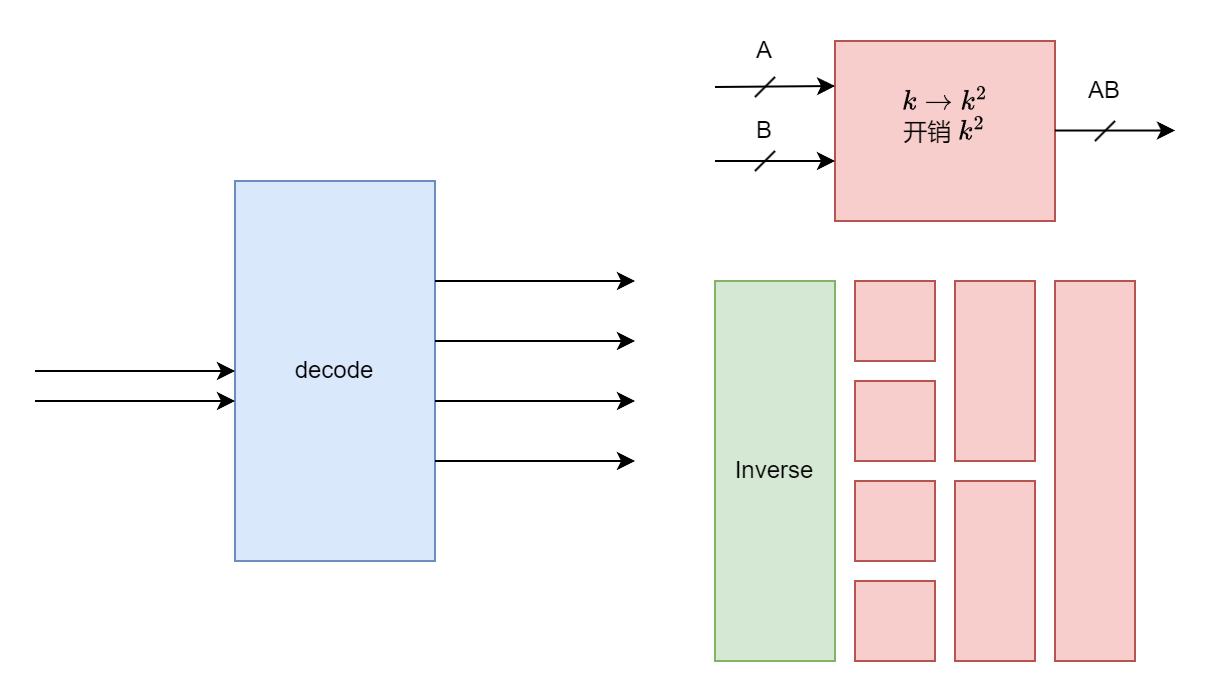
最终化简是如图的一种结构,其中每个红色基础单元输入 2k 个信号,输出 \(k^2\) 个信号,比如 k = 4 输入 \(AB\), \(\bar{A}B\), \(A\bar{B}\), \(\bar{A}\bar{B}\),\(CD\), \(\bar{C}D\), \(C\bar{D}\), \(\bar{C}\bar{D}\) 八个信号,即输入 A、B 与项以及 C、D 与项,输出 A、B、C、D 的与项一共 16 个。基础单元所用到的逻辑门数量等同输出信号个数 \(k^2\) 个。总体通过类似树结构连接。列举出求和公式后发现并不好得到解析解,这里运用数值方法求和。
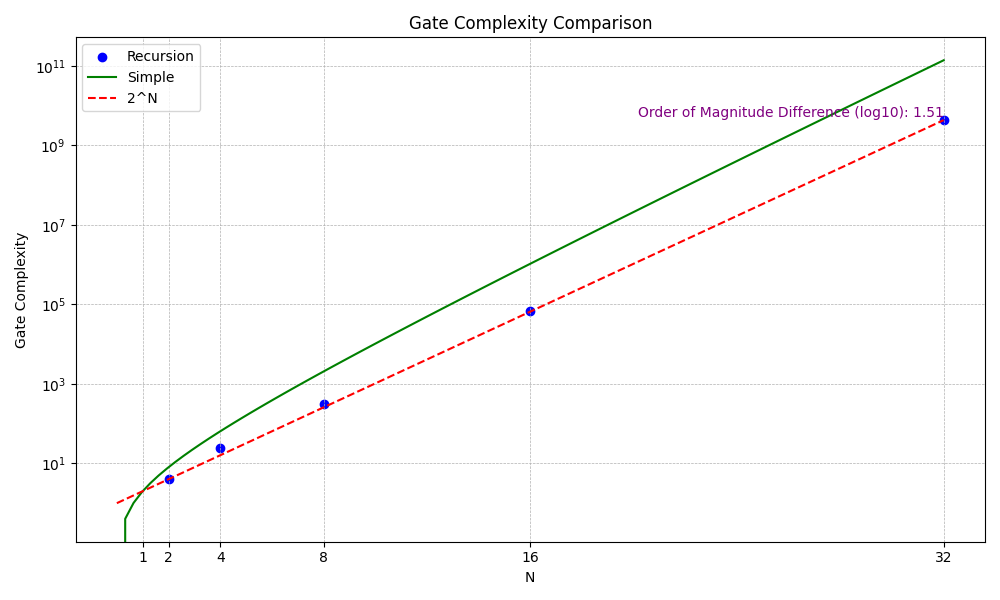
Simple 是满足 \(2^N \times N\) 的函数关系,蓝色点则是数值求和结果,近似符合 \(2^N\) 的红色虚线,所以这部分红色单元的开销大致在 \(2^N\) 个与门这个量级。
当然这种树结构要求输入信号必须是 2 的指数,所以实际结构应当是介于红色虚线和绿色实线之间的某条曲线。
综上,decode 一共需要 \(N\) 个非门,\(2^N\) 个与门。逻辑实现的 MUX 需要大致 \(N\) 个非门和 \(3\times 2^N\) 个与门, 即 \(2N+12\times 2^N\approx 12 \times 2^N\) 个晶体管。
MUX:三态实现
如图是 MUX-4 的 schematic,控制传输门的信号连线没有画出来。通过传输门和来汇聚信号,同时tree的每级之间插入了非门以提高驱动能力。和逻辑门相比,传输门不需要经过mask,而选择信号也可以直接输入到多级tree中进行控制。该实现一共包括 \(N+2^{N}-1\) 以及 \(2^{N+1}-2\) 个传输门,总计是 \(2N+6 \times 2^N -6\approx 6 \times 2^N\) 个晶体管。
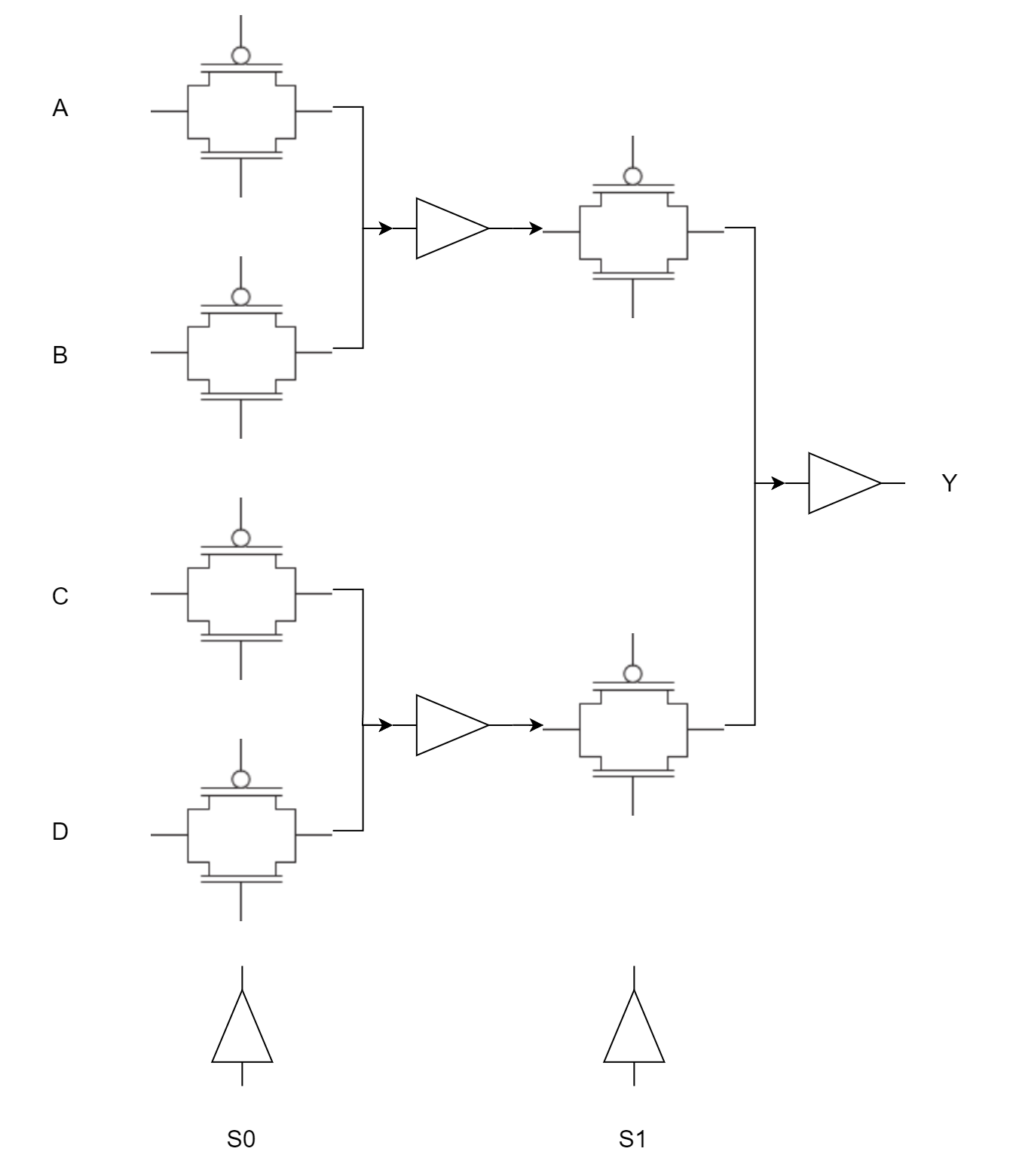
相比逻辑实现,三态实现减少了一半的晶体管数量。
设计中的三态
CMOS 电路一般而言是不提供高阻态状态的,要提供高阻状态就得有特殊的电路安排,可是那样就使芯片上的电路单元不规整划一了……对于像这样的电路的实现,现在采用的策略是将其做成标准件供程序员选用,但不向程序员开放高阻状态,以免滥用——《香山源码剖析》5.1 组合电路
本文是读到以上文字才发觉自己根本不了解实际 Mux 的实现,但我现在仍有俩个疑惑:
- 为何高阻态会使得电路单元不规整划一?也许这要从 layout 的角度学习,像传输门这种连接方式也许会使得布局布线带来额外困难
- 初读以为“不开放高阻”是将高阻包装在标准元件里,输入输出端都是二态信号,但实际上 PDK 中也有提供高阻输出的 buf 标准单元,而 verilog 中高阻态实现的总线也能正常经过 VCS 和 DC 仿真。这里不开放究竟所指何物?