Perface
模拟赛不会被冲烂了。
Problem I
从 \((0,0)\) 到 \((n,m)\) 方案数。
解法:
\(C(n+m,m)\)。
Problem II
从 \((0,0)\) 到 \((n,m)\) 方案,但是不能经过 \(y=x+b\) 的直线。
解法:
考虑映射法。
以一条路径第一次碰到直线的位置为起点,之后所有的路线和 \(y=x+b\) 对称,这样可以不重不漏的映射完每一条路线。我们发现,这些路径的终点都是 \((m-b,n+b)\)。
答案为:\(C(n+m,n)-C(m+n,m-b)\)
Problem III
从 \((0,0)\) 到 \((n,m)\) 方案,但是不能经过 \(y=x+b\) 和 \(y=x+c\) 的直线。
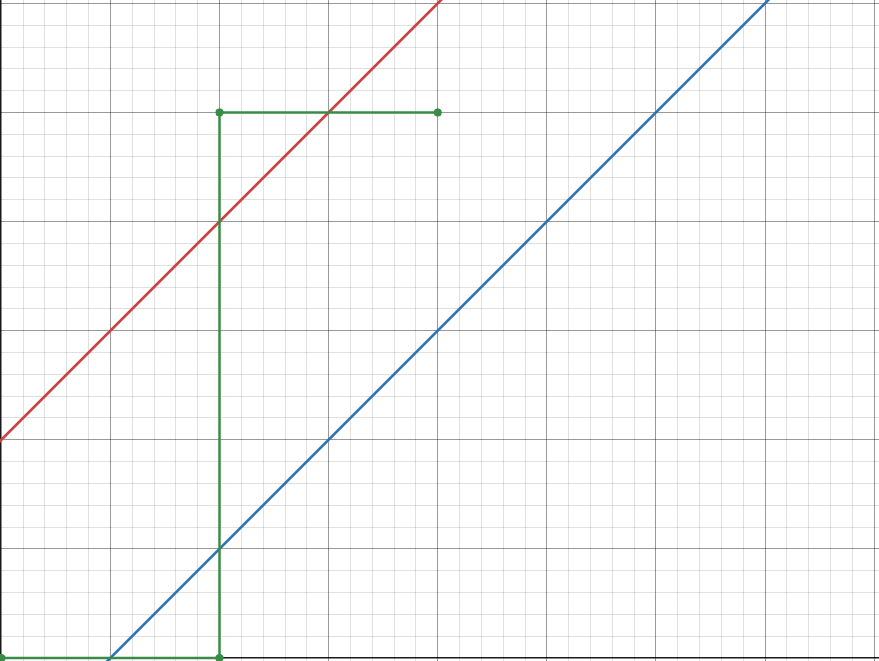
当第一次碰到蓝色线段时,我们进行翻折。
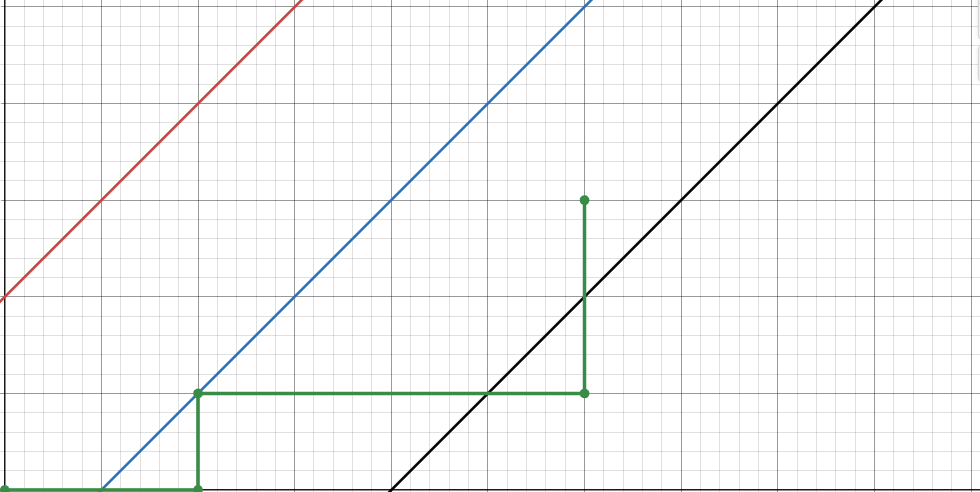
碰到红色线段,也就是对称的黑色线段时,再次翻折。
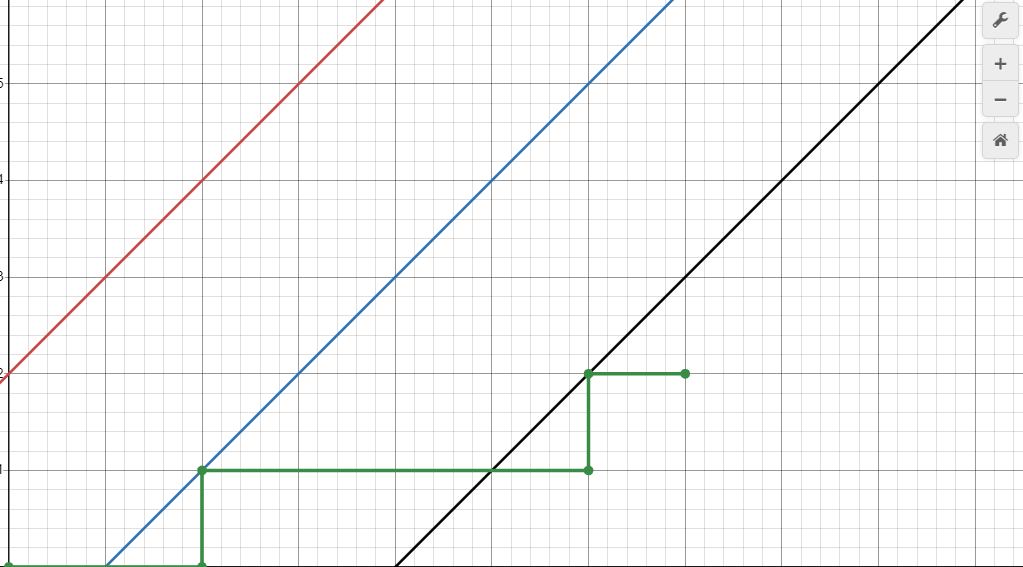
因此,穿过两次线段的我们也映射完了。
观察一下,本质上就是将终点与线段进行对称。
对于一条线依次经过了 \(y=x+b\),\(y=x+c\),记反射序列为 \(bc\),但是如果经过一条线两次 \(bbc\) 我们也看做 \(bc\),因为我们记第一次碰到折线为对称点做到不重不漏。
那么,答案就是 \(ans=\empty-b-c+bc+cb-bcb-cbc+bcbc+cbcb-...\) (容斥原理)
因此,我们需要推出一个对称点的公式,快速求出 \(cbcbcb\) 点的对称坐标。
不难发现,本质上就是线和终点关于线对称,不清楚的直接看图:
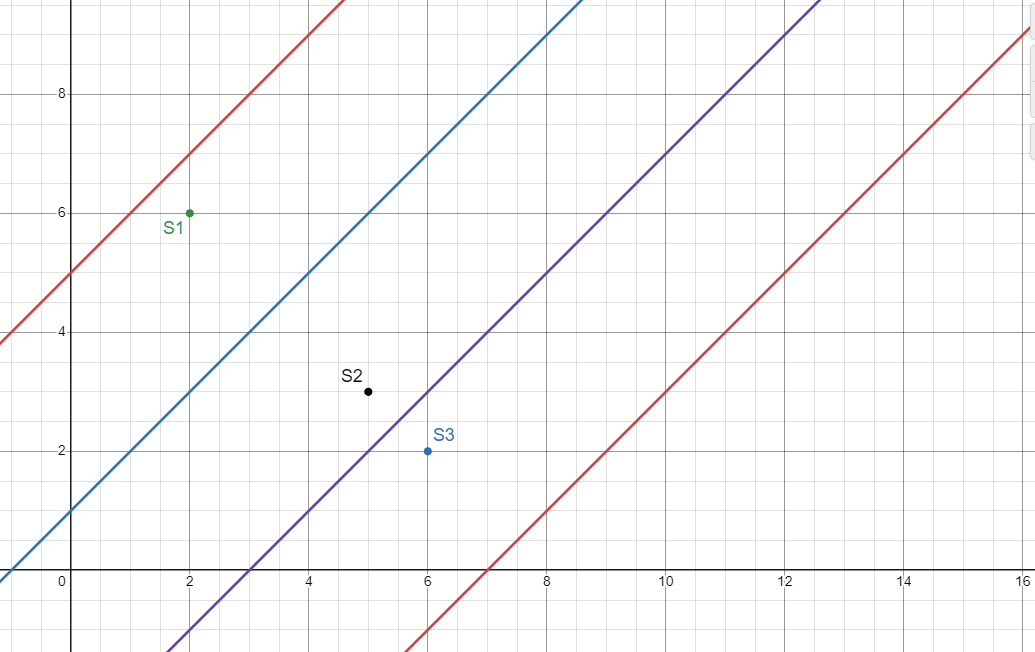
容易知道一个点 \((x,y)\) 对于 \(y=x+b\) 对称点为 \((y-b,x+b)\),直线为 \(y=x+c\) 变为 \(y=x+2b-c\),我们只需要动态维护两条直线然后模拟即可。
考虑边界情况。不难发现每两次坐标会变化 \(2|b-c|\),也就是时间复杂度为 \(O(\frac{n+m}{|b-c|})\)。
被创飞了。






![[OI] 树链剖分](https://img2024.cnblogs.com/blog/3389876/202410/3389876-20241005171153009-303328717.png)