PAIRDISTILL: 用于密集检索的成对相关性蒸馏方法

在当今海量数据时代,有效的信息检索(IR)技术对于从庞大数据集中提取相关信息至关重要。近年来,密集检索技术展现出了相比传统稀疏检索方法更加显著的效果。

现有的方法主要从点式重排序器中蒸馏知识,这些重排序器为文档分配绝对相关性分数,因此在进行比较时面临不一致性的挑战。为解决这一问题,来自国立台湾大学的研究者Chao-Wei Huang和Yun-Nung Chen提出了一种新颖的方法——成对相关性蒸馏(Pairwise Relevance Distillation, PAIRDISTILL)。

PAIRDISTILL的主要研究目的是:

1. 利用成对重排序的优势,为密集检索模型的训练提供更细粒度的区分。
2. 提高密集检索模型在各种基准测试中的性能,包括领域内和领域外的评估。
3. 探索一种可以跨不同架构和领域进行一致性改进的方法。

方法改进详细描述

PAIRDISTILL方法的核心思想是利用成对重排序器提供的细粒度训练信号来增强密集检索模型的训练。该方法的主要组成部分包括:

成对重排序:与传统的点式重排序不同,成对重排序同时比较两个文档,估计一个文档相对于另一个文档与查询的相关性。形式上,给定查询q和两个文档di和dj,成对重排序器估计的概率为:

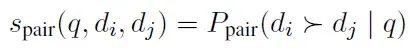
这种方法通过仅建模di和dj的相对相关性来缓解校准问题。

成对相关性蒸馏:PAIRDISTILL的目标是让密集检索器模仿成对重排序器的输出分布。密集检索器预测的成对相关性分布定义为:

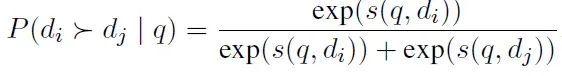
训练目标是最小化密集检索器和成对重排序器的成对相关性分布之间的KL散度:

 

https://avoid.overfit.cn/post/4e825b6cc5b44ce7962f59c873afb7e4