P10418 [蓝桥杯 2023 国 A] 相连的边 题解

一个比较有趣的树形 DP，情况比较多。

【题目简述】

给定一棵树，求三条相连的边，其边权之和最大。

【思路】

以 X 代表当前节点，S 表示儿子，G 表示孙子，P 表示父节点。

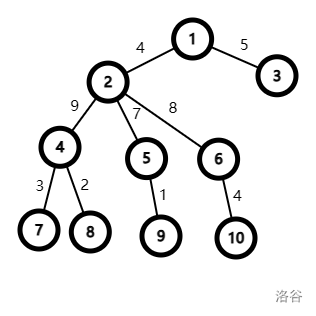
首先把树建出来，在以下图中，我们模拟二号点的 DP 过程，考虑以下几种情况：

• 有一条边指向父节点时

  • FG（Father Grandson）：一条边指向父节点，另外两条边指向孙子。

    需要维护指向孙子的路径的最大值。

    

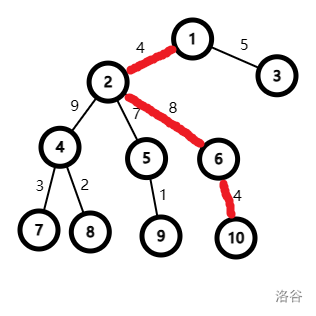
  • FSS（Father Son Son）：一条边指向父节点，另外两条边指向两个不同的儿子。

    需要维护指向儿子的路径的最大、次大值。

    

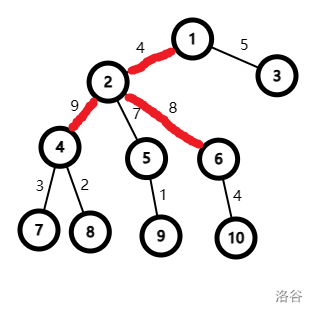
• 没有边指向父节点时

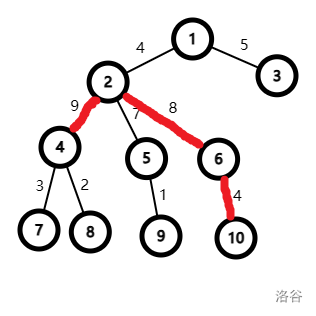
  • GS（Grandson Son）：一条边指向孙子，另外一条边指向另一个儿子。

    需要维护指向儿子的路径的最大、次大值和指向孙子的路径的最大、次大值（可能这两条路径重合）

    

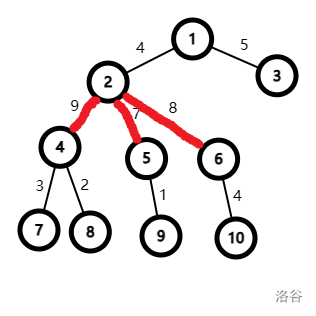
  • SSS（Son Son Son）：三条边指向三个不同的儿子。

    需要维护指向儿子的路径的最大、次大、第三大值。

    

• 要维护的东西：指向儿子的路径的最大、次大、第三大值，指向孙子的路径的最大、次大值。

于是代码就很好写了。

【Code】

#include <bits/stdc++.h>
#define int long long
using namespace std;vector<pair<int,int>>Edge[200005];
int n,u,w,ans;int DFS(int u,int fa,int W){int max11=0,flag11=0,max12=0,flag12=0,max13=0,flag13=0; //max1x,flag1x：向 Dis(X,S) x 大值及儿子编号 int max21=0,flag21=0,max22=0,flag22=0;                  //max2x,flag2x：向 Dis(X,G) 的路径的 x 大值及儿子编号 for(auto it:Edge[u]){int v=it.first,DisXS=it.second;if(v!=fa){int DisSG=DFS(v,u,DisXS);  //Dis(S,G) 的最小值//如果儿子还有儿子（有孙子），更新到 Dis(X,G) 的最大、次大值 if(DisSG!=0){int DisXG=DisXS+DisSG;if(max21<DisXG)      max21=max21,flag22=flag21,max21=DisXG,flag21=v;else if(max22<DisXG) max22=DisXG,flag22=v;}//更新到 Dis(X,S) 的最大、次大、第三大值  if(max11<DisXS)      max13=max12,flag13=flag12,max12=max11,flag12=flag11,max11=DisXS,flag11=v;else if(max12<DisXS) max13=max12,flag13=flag12,max12=DisXS,flag12=v;else if(max13<DisXS) max13=DisXS,flag13=v;}}//W 表示到父节点的路径长度 if(u!=1)           ans=max(ans,max21+W);                 //FGif(u!=1)           ans=max(ans,max11+max12+W);           //FSSif(flag11!=flag21) ans=max(ans,max11+max21);             //GS（两条路径不重合） if(flag11==flag21) ans=max({ans,max11+max22,max12+max21}); //（两条路径重合，其中一条选择次长路） ans=max(ans,max11+max12+max13);                          //SSSreturn max11;
}signed main()
{scanf("%lld",&n);for(int v=2;v<=n;v++){scanf("%lld%lld",&u,&w);Edge[u].push_back({v,w});Edge[v].push_back({u,w});}DFS(1,0,0);printf("%lld",ans);return 0;
}

【闲话】

祝所有看到这篇题解的人 CSP2024 RP++！