SS241007C. 步行(walk)
题意
给你一个 \(n \le 3 \times 10^5\) 个结点的树,每个结点有一个权值 \(a_i\)。有 \(m \le 1.5 \times 10^6\) 次询问,每次删除一条边,然后再连上一条边。如果修改后的图不是树输出无解。否则找出一条路径,满足每个点恰好经过 \(a_i\) 次,问路径权值最大是多少。路径权值指路径路程长度加上终点到起点的距离,即回路的路程长度。\(s=\sum a_i \le 10^{12}\)。询问独立。
思路
首先你不知道走这些点的顺序,因此考虑贪心,然后你就发现贪心假上加假,很难做。
考虑先算原图的答案,每次询问快速更新答案。
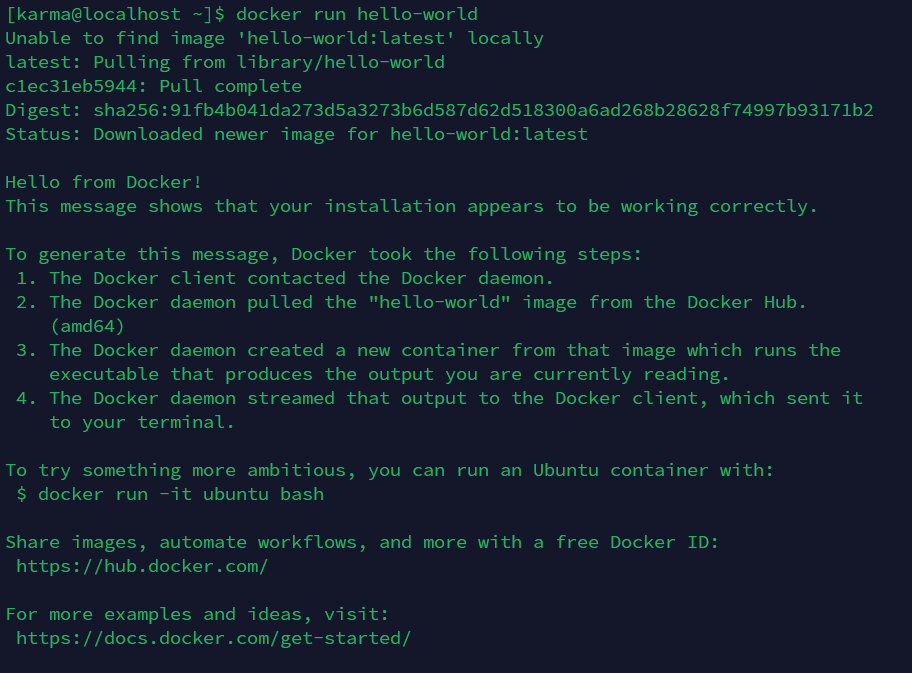
然后考虑拆开每条边的贡献,设 \(sz_u\) 表示 \(u\) 的子树的权值之和。一条边 \(e_i\) 的贡献上界是 \(2\min(sz_u,s-sz_u)\)。可以自行画图理解。如图 1。
然后结论是存在一种方案使得每条边都达到贡献上界。
一个经典的结论是,每条边被经过次数的上限为两侧权值和较小的值,而取带权重心后,在多个子树之间来回跳跃即可构造目标路径,也就是说我们完全能取到上界。
题解是这么证明的。然后讲我的理解。
选定一条边 \(e\),上端点是 \(u\),下端点是 \(v\),来回走它,上去又下来,下来又上去。这条边把图分成上下两部分。如图 2。假设上部的权值和较小,【走到上部,再走下去】这种操作的次数就恰好是权值和次。对于与 \(u\) 相连的边 \(e'\),上部一定比下部小,因此给 \(e'\) 分上部权值次数的操作机会,就恰好能构造 \(e'\) 的贡献的上界。因此上部所有边都可以构造上界。
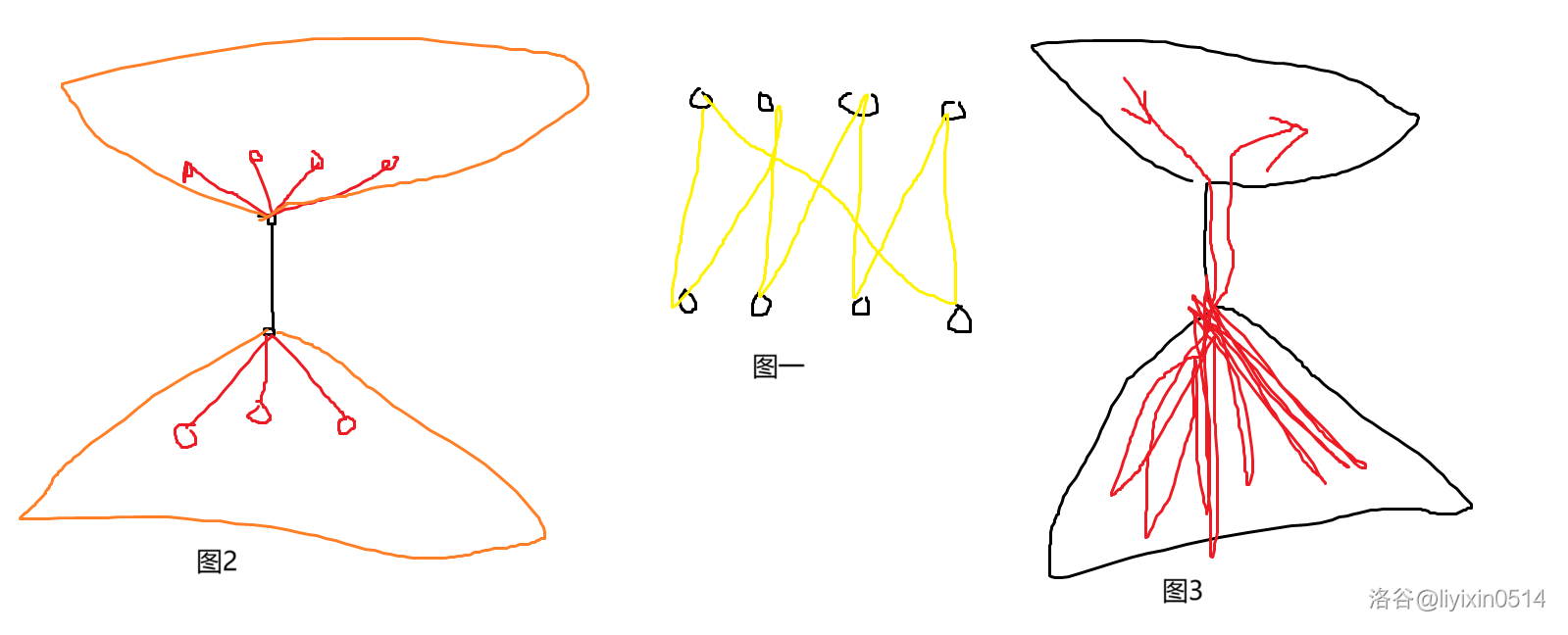
对于下部,【走到下部,再走上去】这个操作的次数恰好是 \(e\) 的上界次。对于与 \(v\) 相连的边 \(e'\),\(e'\) 的上界可能大于 \(e\) 也可能小于 \(e\) 的上界。假设是大于,那么把操作全部分给 \(e'\),然后取其中一次操作,走到下部后,回到 \(v\),然后再走到下部某个儿子,再回到 \(v\),重复若干次,最后上到上部。如图 3。反正操作够就分给 \(e'\),分完不够就取一个操作多刷几次,每次刷可以给一个 \(e'\) 带来 \(2\) 的次数,因为每条边的上界都是偶数,因此总会有一种刷法。
考虑删边和加边,我们需要维护每个点的 \(sz\)。
删除 \((a,b)\),加入 \((c,d)\)。
判无解就判一下是否存在边 \((a,b)\) 以及用 dfs 序判一下 \(c,d\) 是否恰好一个在上部一个在下部即可。
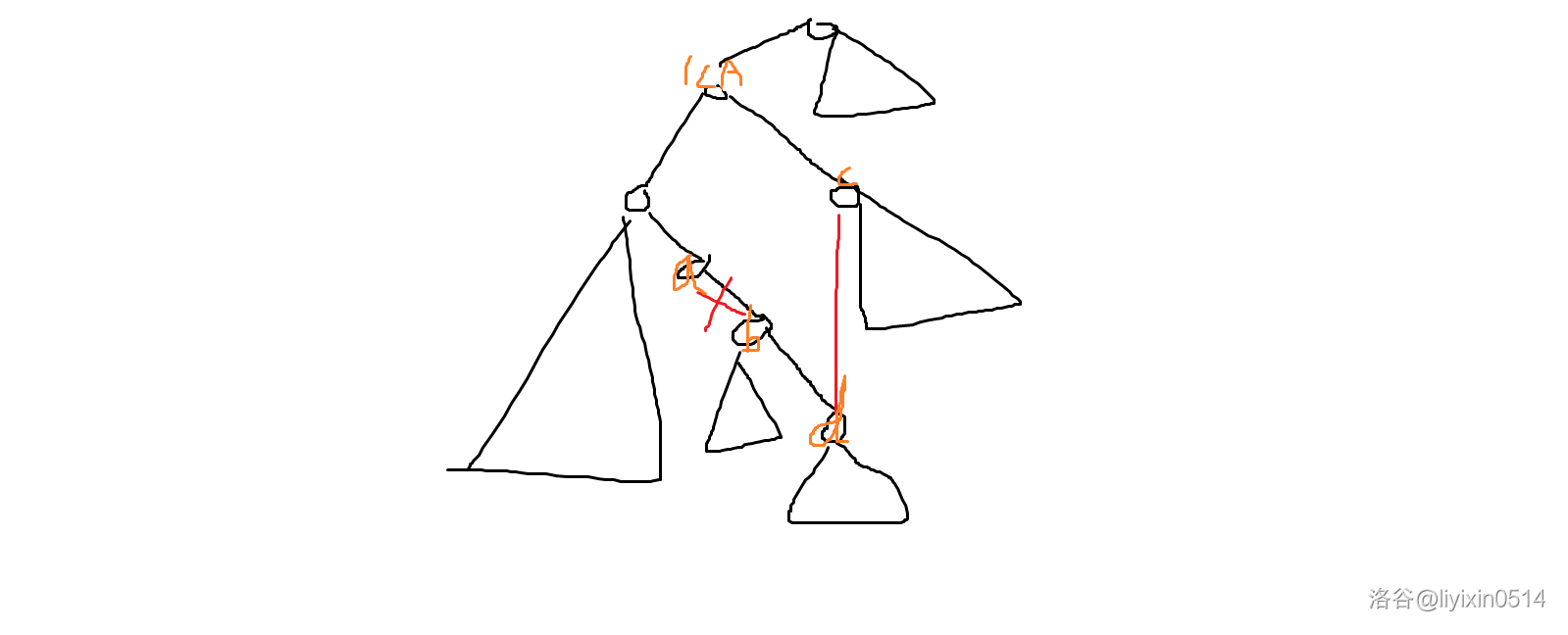
- 对于 \([a,lca)\) 的点 \(u\),\(sz_u-sz_b\)。
- 对于 \([c,lca)\) 的点 \(u\),\(sz_u+sz_b\)。
- 对于 \([b,d]\) 的点 \(u\),设 \(u\) 在链 \([b,d]\) 上的儿子是 \(v\)(\(d\) 在链上没有儿子),\(sz_u\gets sz_b-sz_v\)。
- 对于其他点,\(sz\) 不变。
当然我们不能暴力修改所有点。
比较烦人的是一个点(一个点对应它向上连父亲的那条边)的贡献是 \(2\min(sz,s-sz)\)。我们发现一条链上的 \(sz\) 是单调的。把贡献变成 \(2 (sz+ \min(0,s-2sz))\) 比较方便。
因此我们要处理出三条链的 \(\sum sz\),以及找到 \(2sz=s\) 的分界点,然后加上一部分的 \(s-2sz\)。可以倍增处理。
对于要找链上的儿子,相对复杂的第 3 种链,考虑一个转化。令 \(sz_u\gets sz_b-sz_u\),那么 \(sz_d\gets sz_b\),然后我们求 \([d,b)\) 这条链就行了。
时间复杂度是 \(O((n+m) \log n)\)。
code
被卡常了 qwq,只有 76pts。
把 map 改成二分可以变成 85pts,慎用 STL。