个人主页:平行线也会相交
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创
收录于专栏【手撕算法系列专栏】【LeetCode】
🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望对大家有所帮助
🍓希望我们一起努力、成长,共同进步。
点击直接跳转到该题目
目录
- 题目描述🍬
- 算法原理🎂
- 代码实现🥣
题目描述🍬
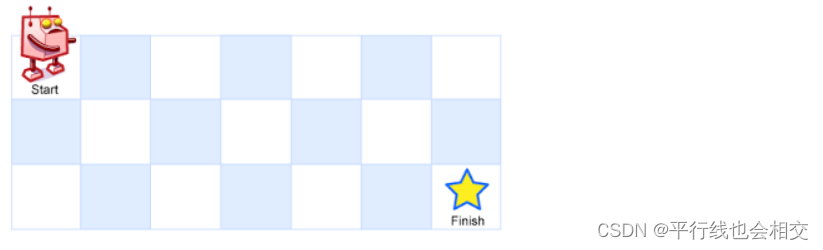
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例一:
输入:m = 3, n = 7
输出:28
示例二:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右
- 向下 -> 向右 -> 向下
示例三:
输入:m = 7, n = 3
输出:28
示例四:
输入:m = 3, n = 3
输出:6
算法原理🎂
状态表示:
dp[i]表示以
[i,j]位置为结尾时有几种路径方式。
状态转移方程:
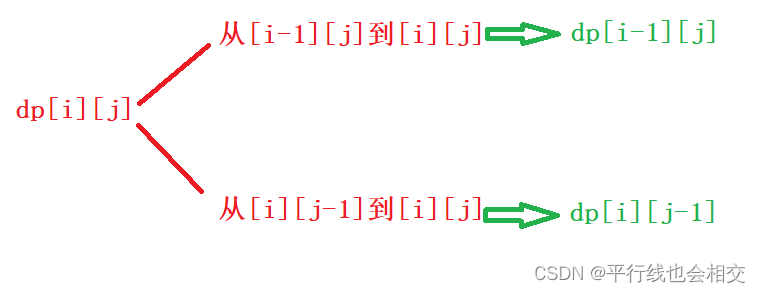
根据最近的一步来划分问题。
所以状态转移方程为:
dp[i][j]=dp[i-1]+dp[i][j-1]。
初始化:
这里初始化的时候要注意:
1.虚拟节点里面的值要保证后面填表的结果是正确的。
2.一定要注意下标的映射关系。
返回值:
根据题意可以得知返回dp[m][n]。
代码实现🥣
class Solution {
public:int uniquePaths(int m, int n) {//创建dp表//初始化//填表//返回值vector<vector<int>> dp(m+1,vector<int>(n+1));dp[0][1] = 1;for(int i = 1; i <= m; i++)for(int j = 1;j <= n;j++)dp[i][j] = dp[i-1][j]+dp[i][j-1];return dp[m][n];}
};
本文至此结束,再见啦友友们!!!