广角镜头,甚至超广角镜头已经成为了现在手机的标配,这样的手机能够拍摄出宽广的视角,还能够在合拍时拍下更多的人物。

比如最新的iPhone13 Pro就有一颗26mm焦距的广角镜头,还有一颗13mm焦距的超广角镜头。

事实上,自2019年起,很多手机摄像头的FOV就已经超过100度了
然而,广角镜头也会带来副作用,如下图红框所示,本来是直线的墙顶却变成了曲线

下面这个场景更加明显,整个地面和大楼都变成弯曲的了

另外,广角镜头拍摄的画面在四角处还会出现拉伸现象,比如这两位姑娘的脚就被明显拉长了。有时候摄影师利用这种特性来拍摄大长腿,但如果构图不恰当也会导致比较诡异的现象。

以上两种现象,分别是由于镜头的物理畸变和透视畸变导致的。今天我们来看看两种畸变产生的原因,以及解决方案。
一. 镜头畸变
在以前的文章 29. 小孔相机 和 31. 镜头、曝光,以及对焦(上) 中,我们都假设整个成像符合小孔成像模型
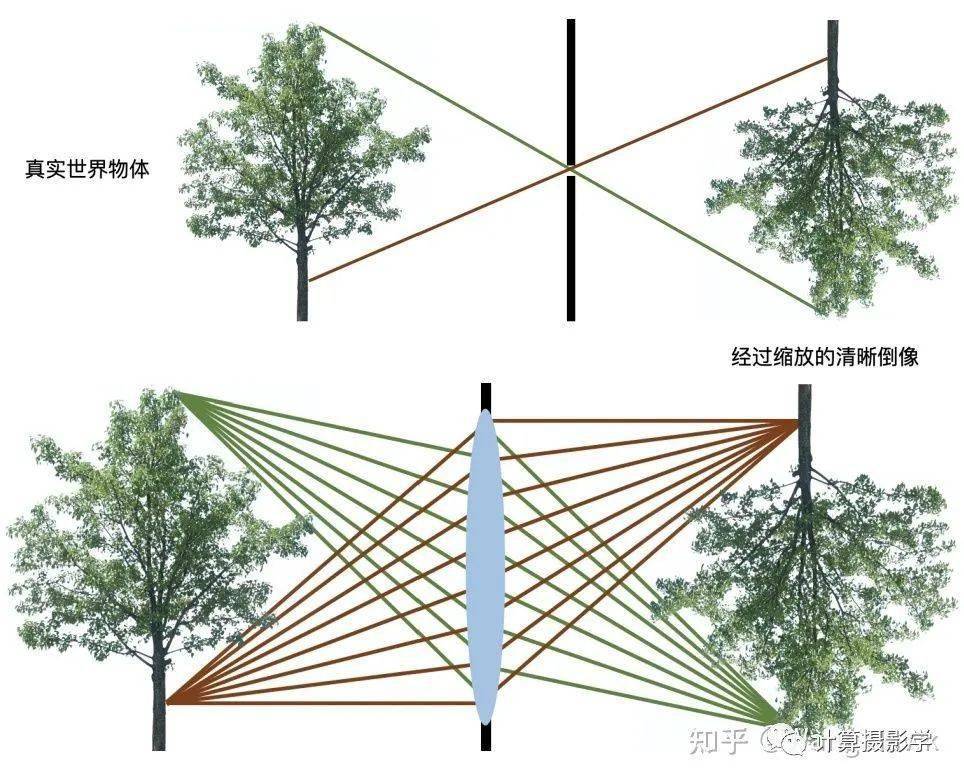
然而,真实的相机的镜头并不能完美的遵循小孔成像模型。
在制造过程中,透镜的实际曲面和理想曲面之间存在一定的误差,这种误差会改变光的折射方向,使得成像点的位置发生偏差,通常这会导致“径向畸变”
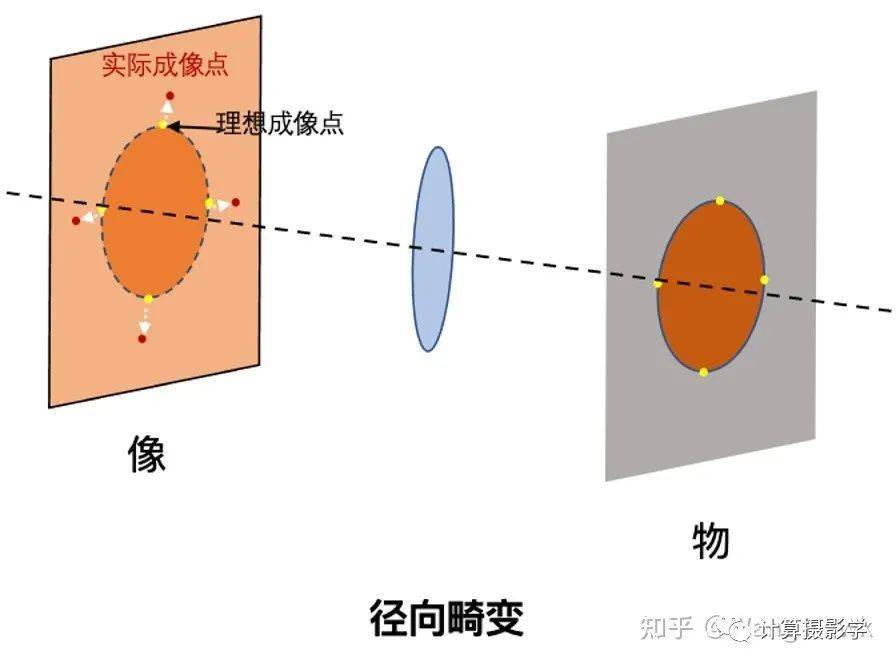
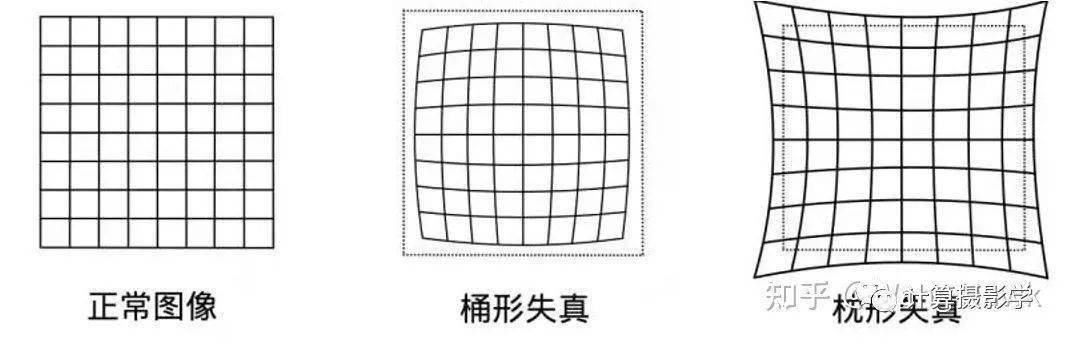
根据透镜曲面的不同情况,径向畸变会导致画面出现桶形失真或枕形失真。
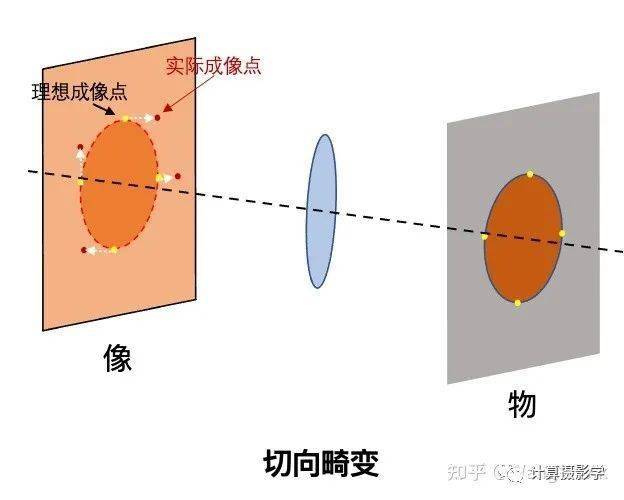
与此同时,实际相机通常采用多个透镜组成镜头组,各透镜中心与光轴是否重合、镜片与光轴是否垂直、各镜片沿光轴方向的位置偏差等都会使光线偏离理论路径。虽然透镜的组合可以相互抵消一些性质相反的非线性畸变,但是也会叠加一些性质相同的非线性畸变。通常,这会导致“切向畸变”
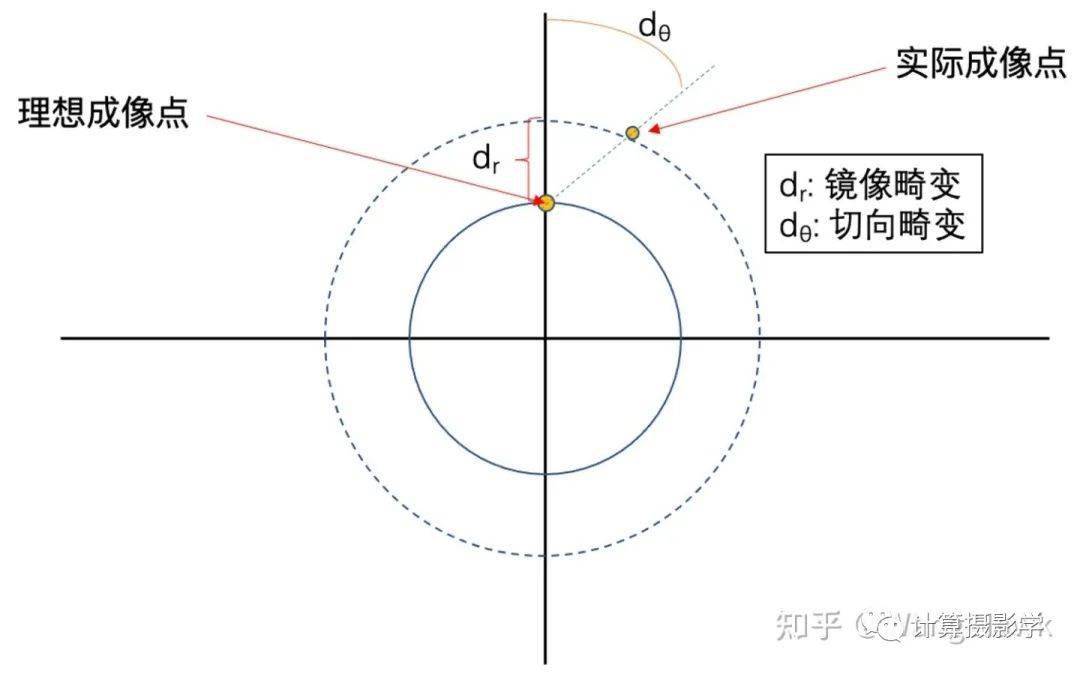
实际成像过程中,这两种畸变通常混杂在一起,尤其是广角镜头组很难避免它们。如下图所示:
那么如何去除镜头畸变呢?
为了去除它们,我们需要严格的用数学公式来表述 实际成像点和理想成像点之间的位置关系。
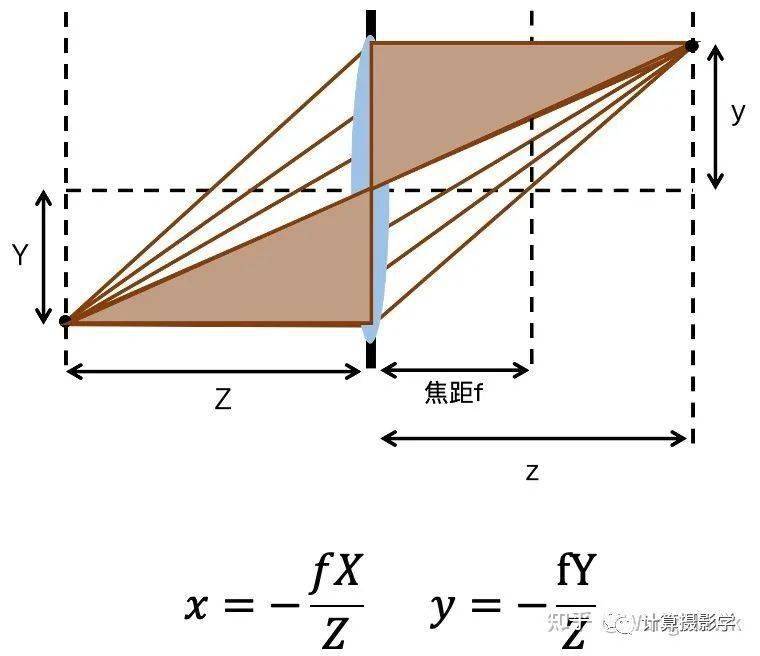
先把小孔成像模型用几何表示如下:
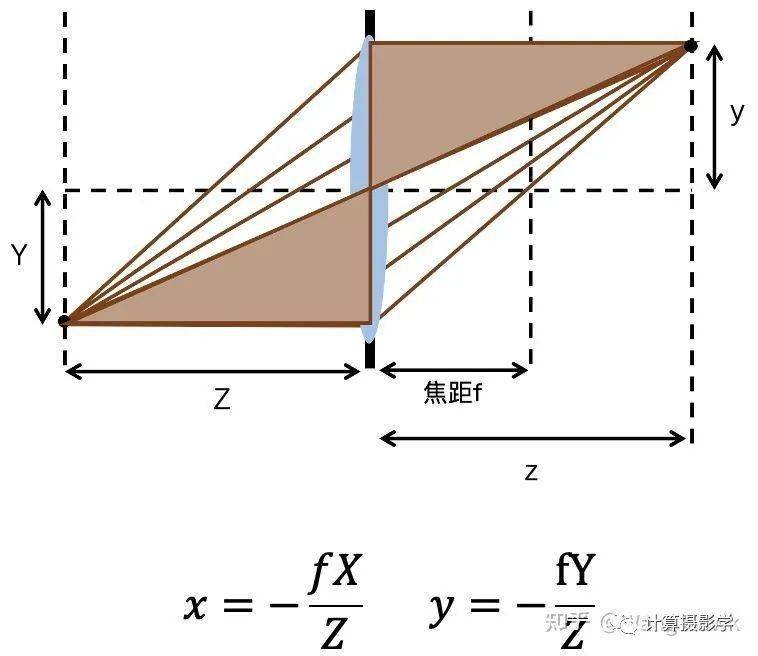
可见对于三维空间中的坐标[X, Y, D]T, 是比较容易求出其理想成像点在相机坐标系中的坐标的,我们令其理想投影点为 [xc, yc],这里,下标c代表corrected(这里是近似认为校正后的坐标既是按照理想小孔成像模型的投影坐标)
由于实际相机会有畸变,所以我们把带畸变的投影点表示为 [xd, yd] ,这是和理想投影点不一样的坐标,d代表distorted。这两个位置的关系可以近似表示如下。这里展示的是3阶模型,更复杂的镜头畸变校正可以用到更高阶的模型,比如OpenCV里面可以用到6阶模型:

这样我们就建立了在相机坐标系下,校正前和校正后坐标之间的关系。由于我们是对图像上的像素进行操作,还需要将相机坐标转换为像素坐标,求取像素坐标之间的关系,这需要用到图像的内参数(参见 手机中的计算摄影1-人像模式(双摄虚化) )
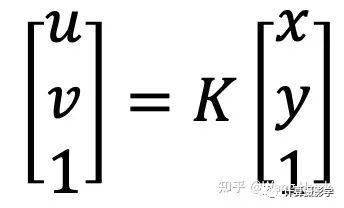
这样我们最终可建立[uc, vc]和[ud, vd]之间的一一对应关系,这种关系可以用一张两通道的图来表述,两个通道分别表示特定校正后像素对应的校正前的u坐标和v坐标。通常,计算出的坐标值[ud, vd]是浮点值,因此需要用到插值算法来实现真正的图像变换。
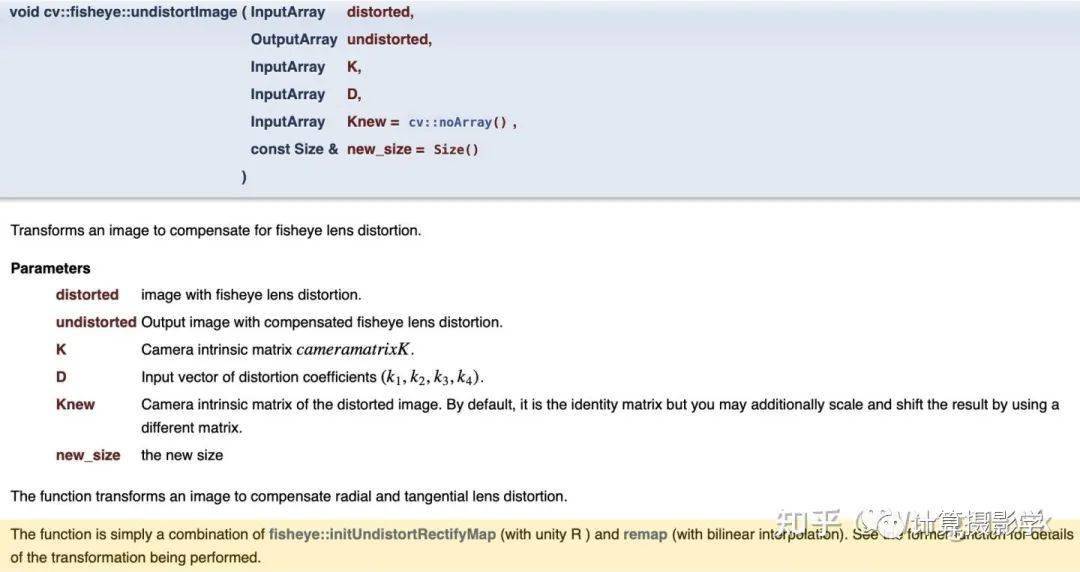
OpenCV的undistortImage函数的帮助文件里也讲得很清楚,它通过相机内参计算出畸变校正的变换图,接着调用remap函数来进行从畸变图像到校正后图像的插值变化。
通过这种方法去除镜头的径向畸变和切向畸变后,画面中的直线会被校直,如下图所示:

采用类似原理甚至可以对鱼眼镜头图像进行畸变校正:

然而,虽然这个方案能很好的校直直线,却也带来了一定副作用。如下图红框所示的腿部,图像出现了异常的拉伸现象:

这是因为实际拍摄的场景中,除了镜头畸变导致的画面形变外,还有一种特殊的畸变: 透视畸变
二. 透视投影和透视畸变
让我们再看看小孔成像模型,可以很容易发现一个物体所成像的尺寸与其距离镜头的距离(物距)成反比,即所谓的 近大远小
当拍摄一个目标时,只要它的表面存在物距上的差异,那么这个物体上每一个物距不同的局部区域都会有不同的成像放大倍率。这种现象不管是通过镜头成像,还是小孔成像都是存在的,是固有的属性,这里的投影模型就叫做透视投影,其产生的效应我称之为透视效应。
人们有时利用透视效应来拍摄有趣的摄影作品:


透视投影还会使得三维空间中的平行线在画面中相交,其交点称作为消失点。


艺术家早就会使用透视技术,来突出主体了,例如下面这幅画是荷兰著名画家约翰内斯·维米尔(Johannes Vermeer)的作品 钢琴课。画家利用透视效应,将主人公安排在了整个画面几条直线的消失点上,从而实现了突出主体的作用。

然而,透视效应也会导致画面的形变,我们看到拍摄同一个姑娘时,短焦镜头(广角镜头)出现了强烈的透视畸变。这是因为为了拍出同样尺寸的像,短焦镜头拍摄时物距更近,因为透视效应的 近大远小法则,这种形变显得更加明显。尤其是在近距离拍摄时,人脸上鼻子相比脸侧面距离镜头更近,所以鼻子成像时放大得更大,于是人脸就显得更加诡异了。

除了上面这种因为近距离拍摄导致的形变,透视效应还会导致远离相机中心的物体被拉伸,比如下面这张用iPhone13 Mini的广角镜头拍摄的照片。相比起上面因为近距离拍摄导致的形变,这种边缘物体被拉伸的现象是我们更常见的情况。

那么,有没有办法同时去除镜头畸变和透视效应导致的边缘形变呢?就像下面这样:

这就是下一节的内容。
三. 同时去除镜头畸变和透视畸变
在用手机照片时,人们拍的最多的就是人像照,不管是单人的,还是多人合照,正如上面的内容所讲,广角镜头带来了不必要的副作用,尤其是图像边角处的人像被拉扯的现象,这种畸变会在我们强行校直直线,变为透视投影后更加明显。
为了解决人像的这种拉扯现象,以前的方法是利用球极投影(Stereographic projection)或者墨卡托投影(Mercator projection)来对图像进行进一步处理。
几种不同的投影方式的比较
当对画面采用这两种投影时,能一定程度上恢复画面边角头部、脸部的形变,但也会导致背景直线重新弯曲,如下图所示。

以前有很多研究者研究过这个问题,但都没有得到理想的效果。比如[Zorin and Barr 1995]提出的方案,虽然修复了人脸的扭曲,但是也导致了墙面、桌面、显示器等其他物体的扭曲

还有[Carroll et al. 2009]提出的通过优化全局一致性最小化感知失真的方案,以及[Tehrani et al. 2016]提出的通过引入虚拟的相机视角的方案。但这些方案需要手动操作,例如标注突出的边缘或要保留的重要区域,而且有时候无法彻底解决问题。
有没有一种自动的、不需人为干预,还能很好的去除图像中各种畸变的方法呢?有的,这就是我要介绍的这篇文章

这是台湾省的三位才俊施易昌, 赖威昇及梁家恺在2019年发表的文章。他们的想法很直接:既然透视畸变矫正能够校直图像中的直线,而球极投影又能够恢复人脸的形状。那么不如先对图像做人脸分割,对非人脸的背景区域计算透视畸变的校正map,再对人脸部分做球极投影的校正map,然后把两部分的变换map整合到一起,用最终的变换图来对图像进行插值变换:
听起来这是个清晰、直接的想法,然而做起来却很不容易。如下面右图所示,如果简单的把两个map融合到一起,只会得到很糟糕的结果

所以作者认为,应该把变换map的求解看做是一个最优化的问题,通过求解这个最优化问题得到最佳的map,然后利用它对图像进行插值变换,这样才能得到最佳的结果。
最优化总是需要达到某些预期目标的,那么此处的目标是什么呢?我们一起来直观的想一想:
- 首先,校正后的图像在人脸部分是非常接近球极投影的
- 越是靠近图像中心的人脸,越接近透视投影本来的样子
- 人脸在变换前后不应该有异常的尺度变化
- 经过透视投影校直的直线,不应该被球极投影重新变弯曲
因此,作者首先将问题用数学公式表达如下:
这里面,{vi*}是指map中所有的2维向量的集合, vi是第i个像素对应的源像素坐标,而Et则是一个目标函数,通过使Et最小化,就可以求得最佳变换map {vi*}
Et由多项目标函数组成。这里面,首先是人脸目标项Ef , 它是所有人脸处的目标函数值Es,k 之和,正如我们上面的直观感觉,这个目标函数约束了下面几个目标:
- 校正后的图像在人脸部分是非常接近球极投影的
- 越是靠近图像中心的人脸,越接近透视投影本来的样子
- 人脸在变换前后不应该有异常的尺度变化


作者演示了人脸项的作用,当没有这一项目标函数的约束时,所得到的图像有明显的人脸扭曲变形,而加入这一项后结果有很大的改善。

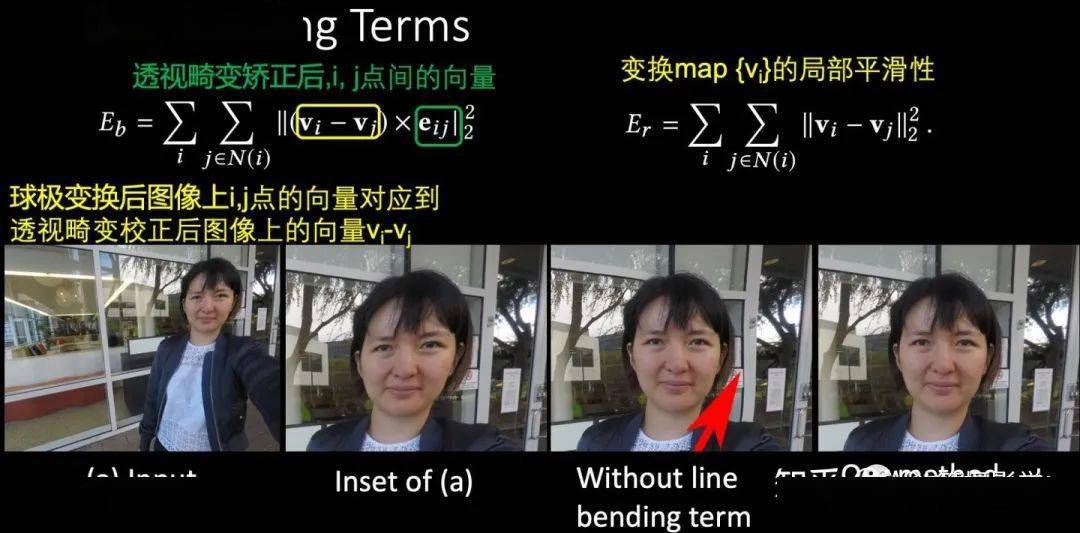
接着需要约束直线的弯曲,目标函数如下。这里用了叉积来约束变换前后直线的夹角,表明允许直线发生平移,但避免发生大的弯曲

然后还要加上1项,约束变换map的局部平滑性
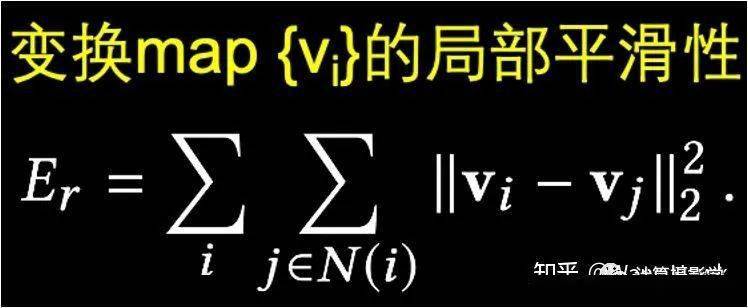
作者也演示了上面这两个约束函数的作用,可见它们很好的保持了直线,而且没有引入副作用。
为了避免在图像边缘处出现异常的扭曲,还需要在中间计算时扩充图像(通过Padding),并对扩充图像做一些特殊的约束(记为Ea ),并在最后一步裁减掉多余的部分。这种边界的约束也带来了收益:

所以让我们回顾下上面讲的最优化式子:
这里的Et就是上述几种目标函数的加权和:
通过使得Et最小化,就可以求出最佳的变换矩阵,这个过程可以图示如下,通常只需要两三个迭代就可以收敛:

作者在大量不同的特质的图像上做了验证,效果非常好。让我们多看一些作者给出的演示下效果吧





四. 实现、性能,以及缺陷
在论文中,作者提到他们将这个算法在PC及高通的SDM845平台上都做了实现,其关键的最优化过程用的是Ceres solver这个库,最终插值算法用的是高精度的Lanczos采样算法。他们将镜头畸变和透视畸变的校正整合到同一个map中进行,对于1200万像素的输入图像, 能够在920ms内完成对所有的畸变校正,并且实际部署到了Google的Pixel 3手机中。一篇论文,不仅仅在理论上有突破点,而且还能实际落地到产品中,有高度的可用性,确实让人佩服!
虽然作者展示的结果已经足够惊艳了,但也并不是完美无缺。作者也提出,它是需要人脸Mask作为输入的,如果没有成功检测、分割到人脸,那么算法就会出错:

另外算法只对人脸部分进行校正,人的身体还是保持不变,这样在校正后有时会出现头小身大的诡异现象:

事实上,我们还发现该算法即便提供了足够的人脸Mask,该算法还是可能导致背景线条出现弯曲,如下图所示:

或是不能对人像做到足够好的修复:

在我看来,它最大的问题还是速度太慢。可能你觉得920ms已经够快了,但事实上对于今天的拍照手机来说,这是一个很慢的速度——用户不能忍受,因而手机生产厂商也无法忍受——大家都希望最好是在更短的时间内,例如几十毫秒内完成整个运算。
有没有能够解决上述效果问题,还能够跑得飞快的算法呢?当然是有的,事实上我的团队已经在手机上实现了效果更好,而且 只需要不到100毫秒就能够完成整个过程的广角畸变校正算法,并且已经在很多客户项目中部署了。而这一部分的基础原理,我将在下一篇文章中为你介绍。
五. 总结
今天我首先为你介绍了镜头畸变,以及它引起的直线弯曲现象。然后讲述了镜头畸变的两种原因——径向畸变和切向畸变,并给出了去除这两种畸变的完整过程。接着我介绍了透视投影的应用,以及它导致的边角拉伸现象。我还花了较大篇幅,介绍了三位宝岛才俊的去除透视畸变的论文。事实上,我们正是基于这篇论文的思想加以改进,实际开发了相关的产品,并已经部署到了很多客户手机中,当然我们已经完全采用了不同的方法。
如同上面的论文中最后所说,广角镜头畸变校正这个方向其实背后还有一个更加本质和深入的问题: 在透视投影下,是图像中的哪些特征使得我们人类视觉系统感知到了畸变呢?有没有某种方式来客观定量的描述这种畸变呢?这其实牵涉到了图像质量的定量评价这个领域了。我希望下一篇文章中,能够对此给出一些解答
独家重磅课程!
1、视觉SLAM必备基础 太卷了!听说学懂ORB-SLAM2课程第3期可全额退款?敢不敢来挑战?
2、 VINS:Mono+Fusion SLAM面试官:看你简历上写精通VINS,麻烦现场手推一下预积分!
3、VIO课程: VIO最佳开源算法:ORB-SLAM3超全解析课程重磅升级!
4、图像三维重建课程(第2期): 视觉几何三维重建教程(第2期):稠密重建,曲面重建,点云融合,纹理贴图
5、 重磅来袭!基于LiDAR的多传感器融合SLAM 系列教程:LOAM、LeGO-LOAM、LIO-SAM
6、系统全面的相机标定课程: 单目/鱼眼/双目/阵列 相机标定:原理与实战
7、深度学习三维重建课程: 基于深度学习的三维重建学习路线
8、激光定位+建图课程: 激光SLAM框架Cartographer课程90+视频全部上线!适合服务机器人!