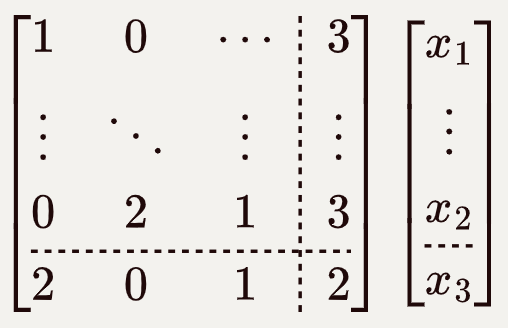
基本应用
读入一个长度为 $ n $ 的由大小写英文字母或数字组成的字符串,请把这个字符串的所有非空后缀按字典序(用 ASCII 数值比较)从小到大排序。
解法
1.将每个后缀取出来,直接排序 \(O(n^2 \log n)\)
2.用hash二分LCP比较下一位,\(O(n \log^2 n)\)
3.倍增求后缀数组,\(O(n \log n)\)
4.高级方法求后缀数组,\(O(n)\)
倍增
先比较每个后缀的第一位,再比较前两位,前四位...
问题在于如何快速比较前两位,前四位。
一个有趣的性质是在比较\(2^k\)位时,我们知道\(2^{k-1}\)位的大小,所以\(2^k\)位的大小只与前一半\(2^{k-1}\)和后一半\(2^{k-1}\)有关,所以可以用基数排序由上一层推到这一层。

基数排序
正常基数排序,是按数位从高到低依次比较大小,比如说三位数,就先比较百位的数字,将百位为 \(0\) 的放在一起,将百位为 \(1\) 的放在一起...。然后,对十位进行比较,在百位为 \(0\) 的里面把十位为 \(0\) 的放在一起,十位为 \(1\) 的放在一起...,最后所有数都有序。
SA的基数排序,就是相当于只有两位数来排序。
代码实现
代码比较抽象要多理解,多思考
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n,m,sa[N],rk[N],x[N],y[N],cnt,num;
char s[N];
void SA()
{for(int i=1;i<=n;i++)rk[x[i]=s[i]]++;//rk辅助数组,x是上一层的排名for(int i=1;i<=m;i++)rk[i]+=rk[i-1];for(int i=n;i>=1;i--)sa[rk[x[i]]--]=i;//正序倒序都可以,sa是排名为i的后缀的起始下标for(int k=1;k<=n;k<<=1){cnt=0;for(int i=n-k+1;i<=n;i++)y[++cnt]=i;//没有后一半是最强的,最靠前的for(int i=1;i<=n;i++)if(sa[i]>k)y[++cnt]=sa[i]-k;//如果可以做后一半,就做//正序枚举,因为y的顺序是后一半从小到大的顺序for(int i=1;i<=m;i++)rk[i]=0;//清零for(int i=1;i<=n;i++)rk[x[i]]++;//根据前一半for(int i=1;i<=m;i++)rk[i]+=rk[i-1];for(int i=n;i>=1;i--)sa[rk[x[y[i]]]--]=y[i],y[i]=0;//后一半更大的在前一半相同时排后面swap(x,y);//y临时存一下上一层x的值。x[sa[1]]=1,num=1;for(int i=2;i<=n;i++){x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?num:++num;//确定这一层的排名}if(num==n)break;//分完了m=num;} for(int i=1;i<=n;i++)cout<<sa[i]<<' ';
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>s+1;n=strlen(s+1),m=150;SA();return 0;
}