CF1802 题解
A likes
最大值一定是一个前缀全部关注, 一个后缀全部取关.
最小值一定是一个前缀关注完立刻取关, 后面全部是关注.
模拟即可.
B Settlement of Guinea Pigs
那些未确定性别的只能每个单独占一个笼子, 其他的需要我们去分配.
如果有 \(m\) 个松鼠被确定性别了, 其中 \(k\) 个是男性, 那么需要 \(\lceil\frac{k}{2}\rceil + \lceil\frac{n-k}{2}\rceil\) 个笼子, 对 \(m,k\) 奇偶分讨即取最大值得答案.
C The Very Beautiful Blanket
由题意得, \(a_{i,j}\oplus a_{i+1,j}\oplus a_{i,j+1}\oplus a_{i+1,j+1} = f_{i\bmod 2,j\bmod 2}\) 只有 \(4\) 种取值, 观察样例发现有数字重复的概率不大, (并且大概率与位运算有关 ps: 正解确实是位运算). 这样的话, 我们只要构造出第一行和第一列的 \(a\) , 并且决策出 \(f\) 的四个值就可以唯一确定整个 \(a\) 矩阵.
如何决策呢? 发现重复的概率并不高, 直接在允许的值域内随机即可.
D Buying gifts
有 \(n\) 个物品 \((a_i,b_i)\) , 需要选择两个不同物品 \(x,y\) , 使得其他的物品要么 \(a_i < a_x\) , 要么 \(b_i < b_y\) , 使得 \(|a_x-b_y|\) 最小.
把它画到二维平面上, 就意味着我们要用两个半平面覆盖所有特殊点, 如图所示.
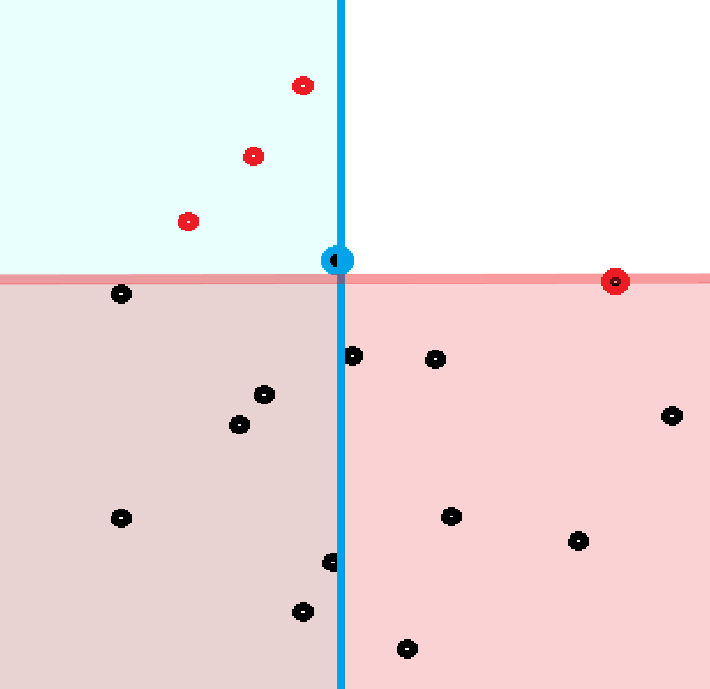
我们枚举 \(x\) (也就是蓝点), 他会覆盖他左边的所有点, 那要想覆盖其他的点, 这个点的 \(b\) 就不能小于右侧红点的 \(b\) (也就是说所有红色点都是合法决策点).
这样的话, 我们用 set 维护左边的所有点的 \(b_i\), 在合法范围内 (高于右侧红点) 寻找最接近于 \(a_i\) 的即可.
注意有 \(a_i\) 相同时的边界情况.
E Music Festival
我们考虑动态规划, 每一段数列能成为最大值的数的个数是有限的, 比如 \([1,3,2,4,5]\) 的可能就只有 \([1,3,4,5],[3,4,5],[4,5],[5]\) 总共 \(4\) 种.
所有可能的这样的序列个数不会很多, 这个数\(cnt \leq \sum n_i \leq 2 \times 10^5\).
发现我们只关心每一个可能段的最小值 \(l_i\) , 最大值 \(r_i\) , 长度 \(w_i\), 因此我们可以把所有的这样的序列收集起来, 按照 \(l_i\) 排序, 再用动态规划去模拟拼接的过程.
这是个类似于二维偏序的 dp , 用 BIT 维护即可.
F The way home
我们发现, 最优策略形如在一个地方 \(x_{i}\) 一直赚钱, 跑路, 在另一个地方 \(x_{i+1}\) 一直赚钱, 跑路...
其中满足 \(c_{x_1} < c_{x_2} < \dots < c_{x_k}\)
这是因为如果后面的 \(c\) 更小, 那么把这次赚的钱放到前面去赚只要更少的次数就能完成, 更优.
这样, 我们设 \(f_{u,best}\) 表示目前走到 \(u\) , 上一次赚钱是在 \(best\) 的最优策略.
一个最优策略用一个二元组表示 \((t_i,re_i)\) 表示目前赚钱 \(t_i\) 次, 剩余 \(re_i\) 块钱.
但是无法比较二元组之间的优劣怎么办?
我们发现贪心的先保证 \(t_i\) 更小, 再保证 \(re_i\) 最大一定更优.
为什么呢? 因为所有方案 \(re_i\) 都会小于 \(c_{best}\) (如果大于等于那就可以少赚一次钱.), 那么 \(t_i\) 小的方案就可以再演出一次得到方案 \((t_i+1,re_i+c_{best})\) , 这个二元组会完爆掉 \(t_i\) 较大的方案, 因此贪心是对的.
这个转移只会从 \(t_i\) 小的转移向 \(t_i\) 大的, 因此用类似于 dijkstra 的方式转移即可.
G Gasoline prices
快跑啊孩子, 这题卡常
我们用并查集去维护相等关系, 然后每一个不一定相等的元素决策, 乘法原理即可.
我们发现有效的相等关系连边只会有 \(n-1\) 次(树的边数是 \(n-1\) ), 这样, 问题转化为如何快速找到有效的连边位置.
我们发现, 对于一次链操作, 我们把每个点的点权看成他的并查集代表元, 如果一个前缀链都是无效的, 那么前缀链的权值连起来形成的串是一样的.
那么我们只要每次都二分+哈希去做就可以了, 维护哈希用树剖就可以了.
最后的问题是一次 merge 好多个点的点权都会变, 怎么办呢? 启发式合并! 两个 log 就做完了.