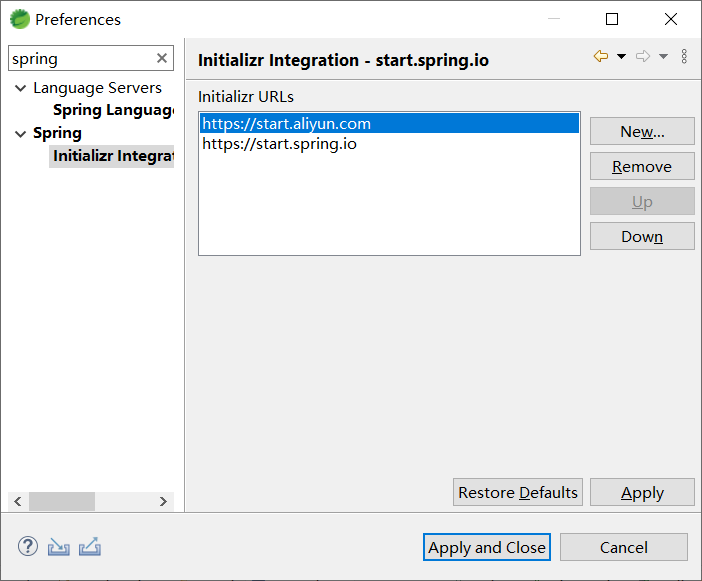
众所周知,在当前机器学习看待数据的很重要一个方式是概率,例如分类问题是建模一个P(Y=C|X)。
在面对离散变量的时候,例如人名这种离散变量。
假设有问题:给一个名字,判断该人是中国哪里人。(或许在现实生活中,该问题是不合理的,一般情况下无法根据人名判断是哪里人)
假设我们有所有省份的人名。我们可以统计不同人名属于某个省份的概率。这个概率可以通过“频率”来计算。
在这里,输入变量“人名”是一个离散型变量。当统计完成后,我们就得到了一个不错的分类模型。
然而,当输入变量是连续型变量的时候,我们无法通过频率来估计概率。连续型变量的概率也没有意义。
例如,从【1,5】这个区间取中任意一个数的概率都是0。因为其样本空间为无穷多。
再用频率去计算就相当于:
这个时候,我们就需要对连续性变量的概率进行描述。
于是就引入了概率密度函数这个概念。
举一个例子:
假设一个电子监控设备在每个小时的开始时会被短暂地打开一次,并且无论设备已经使用了多长时间,它都有0.905的概率能够正常工作。
如果我们让随机变量 \(X\) 表示监控设备首次失效的小时数,那么 \(p_X(k) = \prod_{i=1}^{k} ,P_i\) 是 \(k\) 个独立概率的乘积。
。 绘制成图片如下:
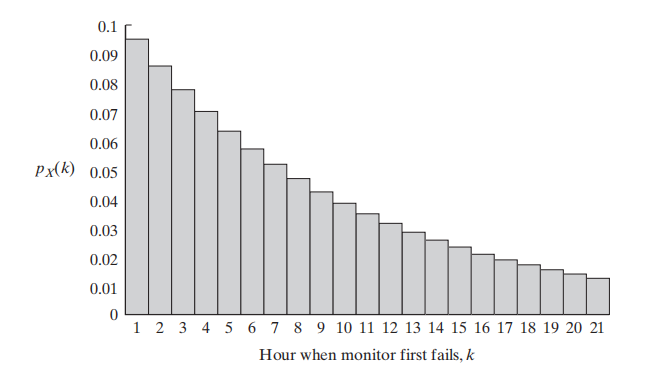
如图是K从1-21不同取值下的概率值。如果我们再加上一条曲线:
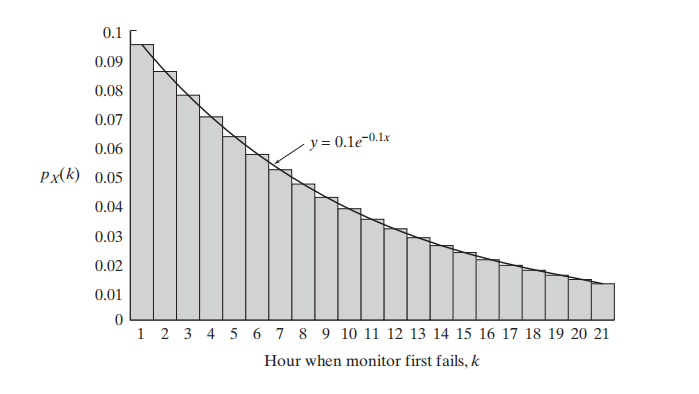
那么很容易得出,任意一段区间[a,b]内,这些柱状体的面积近似于曲线在该区间的积分
函数 \( f(x) \) 在区间 \([a, b]\) 上的积分表示为:\( \int_{a}^{b} f(x) \, dx \)。
该函数就相当于概率密度函数。通常,我们也将该概率密度函数称为连续变量X的分布。
对于一些常见的概率密度函数,我们也有一些名字例如“正态分布”等。
当我们在面对机器学习任务时候,如果要建模的变量对象是一个连续型变量,有时会假设其服从某些常见分布。例如HMM的语音识别中,隐状态序列S的样本空间为有限的。而状态S对应的观测序列,也就是声音的特征向量是连续型变量。
这时候,如果我们想计算隐状态为Si条件下,某个观测状态的概率。由于观测状态是连续型的特征向量,无法直接统计概率。因此,我们假设已知隐状态S的条件下,观测状态为X的概率服从正态分布。这样就把有限个隐状态对应无数个连续型变量的问题建模为了有限个状态对应有限个不同的正态分布的问题。