Description
有 \(n\) 种蔬菜,对于所有的满足条件 \(d\times x_i \leq c_i\) 的正整数 \(d\) ,有 \(x_i\) 个单位的蔬菜将在 第 \(d\) 天结束时变质。
特别地,若 \((d - 1)\times x_i \leq c_i < d\times x_i\) ,则有 \(c_i - (d - 1)\times x_i\) 单位的蔬菜将在第 \(d\) 天结束时变质。
注意,当 \(x_i = 0\) 时,意味着这种蔬菜不会变质。
同时,每天销售的蔬菜,总量也是有限的,最多不能超过 \(m\) 个单位。
现在,小 N 有 \(k\) 个问题,想请你帮忙算一算。每个问题的形式都是:对于已知的 \(p_j\),如果需要销售 \(p_j\) 天,最多能获得多少收益。
\(n,p_j\leq 10^5,m\leq 10\)。
Solution
首先考虑怎么建出费用流模型。
注意到每天会有蔬菜消失,很难处理,所以考虑时空倒流,这样就变为每天会有一些蔬菜添加进去。
建立源点 \(S\),汇点 \(T\),定义 \((t,i)\) 表示第 \(t\) 天第 \(i\) 种蔬菜对应的点,\([t]\) 表示第 \(t\) 天采购对应的点,则可以连出如下边:
- \((S,(t,i),a_i,\max\{c_i-(t-1)\times x_i,0\})\)
- \(((t,i),(t-1,i),+\infty,0)\)
- \(((t,i),[t],+\infty,0)\)
- \(([t],T,m,0)\)
但是这里没有考虑每种蔬菜第一次买的 \(s_i\) 的贡献,这也是好处理的,只需要将 \(i\) 蔬菜第一次出现的时刻里选一个边的边权变为 \(a_i+s_i\) 即可,容易发现一个蔬菜如果被选就一定优先选这个特殊边。
考虑如何模拟这个费用流。
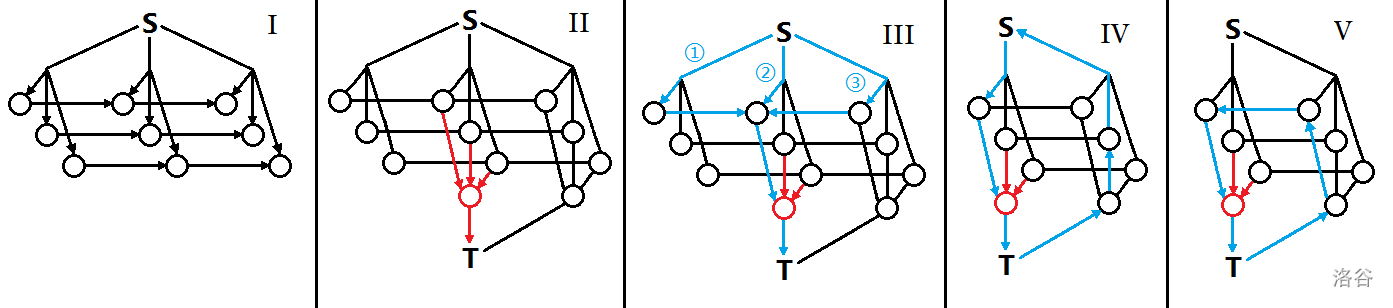
这里用每次加点的方式跑。观察上图会发现只有 II 和 III 种增广路是有效的,而这两种都不会退流,所以 \([1,t]\) 时刻最优解用到的蔬菜一定是 \([1,t-1]\) 的超集,而 \([1,t]\) 的所有蔬菜放到 \([1,t-1]\) 不考虑每天销售限制的话都能用,所以如果求出 \([1,t]\) 的蔬菜,将这些用到的按照权值从大到小排序即可得到 \([1,t-1]\) 的蔬菜。
现在只需要求出 \([1,10^5]\) 所用到的蔬菜即可,同样考虑时空倒流,用一个堆维护目前没被用完的蔬菜的权值和出现次数。注意到我们不能每次都更新每个蔬菜的剩余数量,但是由于只需要找到出现次数至少一次的蔬菜,所以当某个蔬菜删空了再更新数量即可。
时间复杂度:\(O(nm\log n)\)。
Code
#include <bits/stdc++.h>// #define int int64_tusing i64 = int64_t;const int kMaxN = 1e5 + 5, kMaxT = kMaxN * 10;int n, m, k, t;
int a[kMaxN], s[kMaxN], c[kMaxN], x[kMaxN], lst[kMaxN], now[kMaxN];
i64 veg[kMaxT], ans[kMaxT];
std::vector<std::tuple<int, int, int>> vec[kMaxN];int gettime(int c, int x) {if (!x) return 1e5;else return (c - 1) / x + 1;
}void solve() {std::priority_queue<std::tuple<int, int, int>> q;for (int c = 1e5; c; --c) {for (auto [x, w, cnt] : vec[c])q.emplace(w, x, cnt), now[x] += cnt;std::vector<int> vv;for (int cc = 1; cc <= m && !q.empty(); ++cc) {auto [w, i, cnt] = q.top(); q.pop();veg[++t] = w, --now[i], --cnt;if (cnt) q.emplace(w, i, cnt);if (!now[i] && x[i]) {if (lst[i] > c) q.emplace(a[i], i, now[i] += x[i] * (lst[i] - c)), lst[i] = c;else vv.emplace_back(i);}}for (auto i : vv) q.emplace(a[i], i, now[i] += x[i]), lst[i] = c - 1;}std::sort(veg + 1, veg + 1 + t, std::greater<>());for (int i = 1; i <= t; ++i) ans[i] = ans[i - 1] + veg[i];
}void dickdreamer() {std::cin >> n >> m >> k;for (int i = 1; i <= n; ++i) {std::cin >> a[i] >> s[i] >> c[i] >> x[i];vec[gettime(c[i], x[i])].emplace_back(0, a[i] + s[i], 1);--c[i];if (c[i]) {int t = gettime(c[i], x[i]);lst[i] = t;vec[t].emplace_back(i, a[i], c[i] - x[i] * (t - 1));}}solve();for (int i = 1; i <= k; ++i) {int p;std::cin >> p;std::cout << ans[std::min(p * m, t)] << '\n';}
}int32_t main() {
#ifdef ORZXKRfreopen("in.txt", "r", stdin);freopen("out.txt", "w", stdout);
#endifstd::ios::sync_with_stdio(0), std::cin.tie(0), std::cout.tie(0);int T = 1;// std::cin >> T;while (T--) dickdreamer();// std::cerr << 1.0 * clock() / CLOCKS_PER_SEC << "s\n";return 0;
}